ISSN 0798 1015

Vol. 41 (Nº 15) Ano 2020. Pág. 20

Previsão do preço de soja, trigo e milho por meio da metodologia Box & Jenkins

Forecasting soybean, wheat and corn prices using Box & Jenkins methodology

ZIEGLER, Cristiano 1; BRANCO, Antonio N. 2; UEDA, Renan M. 3; LÍRIO, Valentina W. 4; FIEGENBAUM, Tobias P. 5; RODRIGUES, Stéfane D. 6; ZANINI, Roselaine R. 7; SOUZA, Adriano M. 8

Recebido: 03/01/2020 • Aprovado: 23/04/2020 • Postado 30/04/2020

Conteúdo

1. Introdução

2. Referencial Teórico

3. Metodologia

4. Resultados

5. Conclusões

Referências bibliográficas

1. Introdução

A soja, o milho e o trigo são commodities que possuem um papel fundamental na economia do Brasil, pois de acordo com Fliehr (2013), a commodity agrícola é um elemento fundamental da balança comercial brasileira, representando grande parte de suas exportações. Conforme Dall’agnol & Hirakuri (2008) a produção de soja cresceu cerca de 40 vezes nos últimos 48 anos, provocando, juntamente com a cultura do trigo, significativas mudanças na agricultura nacional, pois viabilizaram a implementação desse viés comercial no país. Ademais, segundo os mesmos autores, elas provocaram mudanças na mecanização das lavouras, participando na modernização do sistema de transporte, expansão da fronteira agrícola, profissionalização e incremento no comércio internacional, assim como na consequente urbanização do Brasil.

Segundo Junior (2014) o Brasil atualmente é o maior exportador mundial de soja in natura e o segundo maior produtor do grão, ficando atrás apenas dos Estados Unidos. Ao mesmo tempo, a soja é considerada o cultivo de maior competência da agricultura (27,7 milhões de hectares plantados na safra 2012/2013, equivalendo 52% dos cultivos temporários) e econômico-comercial (9,4% das exportações totais de 2012).

Ao mesmo tempo, de acordo com Caldarelli & Bacchi (2012) o milho possui uma das cadeias produtivas mais importantes para o agronegócio brasileiro, correspondendo a 37% da produção total de grãos. Essa cultura configura esse produto como o cereal mais cultivado no mundo, com produção superior a 840 milhões de toneladas na safra 2009/2010, e produtividade média de 5.194 kg por hectare, sendo o Brasil o terceiro maior produtor mundial, ficando atrás dos EUA e China (Oliveira, Nascente, Kluthcouski & Portes, 2013). Nesse sentido, ambas as culturas são insumos básicos para avicultura e suinocultura, mercados importantes internacionalmente e grandes geradores de receita para o país.

Por outro lado, Camponogara, Gallio, de Borba & Georgin (2015) afirmam que o trigo também caracteriza como importante componente neste quadro, visto que, é uma alternativa para a produção agrícola desses grãos no inverno, além de ser um cereal importante na alimentação humana. Nesse contexto, conforme Silva, Ferreira & Junior (2004), a cadeia produtiva do trigo no Brasil também possui relevância para o setor alimentício, abastecendo parte substancial da necessidade de alimentos da população, como: massas, pães e biscoitos, além disso, é composto para ração animal e ainda representar uma grande fonte geradora de empregos.

Atualmente, o preço dessas commodities é tabelado mundialmente pela cotação do dólar por bushels na bolsa de valores, servindo de referência para precificação da saca nacional desses grãos. Nesse quadro, segundo Haile, Kalkihl & Von Braun (2015) os agricultores optam pelo cultivo de determinada cultura de acordo com o preço pago do produto, apresentando consequente declínio de plantio das culturas de menores cotações. Todavia, tal fenômeno tem impacto direto na inflação do país, pois de acordo com Moreira (2014), a volatilidade dos preços dessas commodities influência nos alimentos, como carne, e derivados da soja e milho. 

Embora apresentem características distintas, o mercado da soja, do milho e do trigo possuem fatores de interação de substitutibilidade na oferta, competindo principalmente pelo fator terra no momento de escolher qual cultivar plantar, ou no caso de complementaridade, na demanda, principalmente na composição de rações. Ao mesmo tempo, existe uma relação entre preço da saca desses grãos, pois se aumentar muito o consumo de uma dessas culturas, ou o seu preço, há impacto direto na demanda pelas outras variedades (Caldarelli & Bacchi, 2012).

Por esse motivo, dada a relevância do tema, o presente estudo tem por objetivo ajustar um modelo de previsão para o preço de soja, trigo e milho por meio da metodologia Box & Jenkins.  Para isso, técnicas de previsão robustas serão utilizadas com a finalidade de entender o histórico dessas cotações, possibilitando descobrir qual modelo matemático melhor representa o comportamento de preço dessas commodities, assim como inferir o impacto futuro de seus valores no mercado nacional no curto prazo.

Nessa etapa é apresentado o que a literatura expõe sobre o assunto em estudo, serão abordados os conceitos de séries temporais, modelos estacionários e não estacionários, modelos fracionários e os modelos sazonais.

2.1. Séries temporais

Segundo Souza, Almeida, Guarnieri, Souza & Lopes (2010) uma série temporal é uma sequência de observações recolhida ordenadamente ao longo do tempo, tendo como principal característica grande dependência entre os dados próximos. Dada suas propriedades, elas possuem qualidades específicas que, segundo os autores, complicam seu estudo. Dentre elas, segundo Moretin & Toloi (1985) estão: presença de tendência, demonstração que ao longo do tempo a série apresentará um sentido; ciclos e sazonalidade, isto é, movimentação com períodos ondulatórios, podendo ser curta ou longa duração; podendo apresentar um erro, conhecido como “ruído aleatório”, contemplando as variações naturais da série e que não possibilite ser modelado. Em decorrência desses fatos, para Souza et al. (2010), grande parte dos métodos estatísticos foi criado para examinar observações independentes, assim, o estudo de séries temporais carece de técnicas específicas.

Para resolver isso, George Box e Gwilyn Jenkins desenvolveram uma das principais técnicas estatísticas que possibilitam análises de séries temporais. Um dos motivos para isso, segundo Marchezan & Souza (2010), é a chance de fazer previsões futuras que, em muitos casos, apresentam melhores resultados quando comparadas às obtidas com base nos modelos econométricos tradicionais. Opinião compartilhada por Hikichi, Salgado & Beijo (2017), pois segundo eles sua aplicação já está consolidada na literatura, sendo aplicada com sucesso nas previsões em diferentes dados e contextos.

De acordo com Marchezan & Souza (2010), o modelo de Box & Jenkins é constituído por um modelo Autoregressivo Integrado de Médias Móveis (ARIMA), que tem por objetivo caracterizar o processo gerador da série ao longo do tempo. Nessa perspectiva, os modelos ARIMA são técnicas matemáticas que objetivam capturar o desempenho da correlação existente na série temporal, chamada também de “Autocorrelação”, permitindo fazer previsões. Neste quadro, Fava (2000) afirma serem os modelos ARIMA o resultado da junção de três elementos, nomeados também como “filtros”: o elemento autoregressivo (AR), o filtro de integração (I) e o elemento de médias móveis (MA), tornando essa configuração a produtora de muitos modelos de previsão.

Nesse cenário, há duas possibilidades para o comportamento das séries temporais, o estacionário e o não estacionário. Para Werner & Ribeiro (2003), uma série é considerada fracamente estacionária se sua média e variância se mantêm constantes ao longo do tempo; assim como um modelo pode ser considerado fortemente estacionário se todos os seus momentos conjuntos são invariantes a translações no tempo. Por outro lado, segundo os autores, um processo é chamado de não estacionário quando apresentar média e variância dependente do tempo.

O emprego do modelo ARIMA é uma maneira de resolver várias adversidades de previsão, pois de acordo com Souza (2006), possibilita previsões certeiras para modelos de séries temporais, sendo indicada para séries de média e grandes quantidades de dados, de no mínimo 50 observações. Nesse contexto, para Hikichi, Salgado & Beijo (2017), o desenvolvimento de modelos Box & Jenkins (1976) tem como base um ciclo, onde a escolha do modelo adequado se fundamenta em sua própria composição de informações. Segundo essa técnica, o ciclo é composto por 4 fases:

a) Identificação: deduzir os valores dos elementos autoregressivos (p), os de médias móveis (q) e da diferença (d);

b) Estimação: momento em que são estimadas as características do modelo;

c) Verificação: aplicação de testes estatísticos para comprovar se os pressupostos da análise de variância são verídicos. Nesta fase, se o modelo não for adequado, o ciclo recomeça;

d) Previsão: última fase do ciclo, momento de fazer previsões futuras com o modelo escolhido.

A aplicação desse procedimento viabiliza descobrir e estimar inúmeras reações na série, tornando essencial para a precisão nas estimações (Amaro & Souza, 2014).

2.2. Séries estacionárias e não estacionárias

Segundo Martins & Werner (2014) a metodologia Box-Jenkins possibilita detectar distintos modelos ARIMA e entre eles: o modelo Autoregressivo de ordem p (AR), o modelo de Médias Móveis de ordem q (MA), o modelo Autoregressivo de Médias Móveis de ordem p e q (ARMA), o modelo Autoregressivo Integrado de Médias Móveis, de ordem p, q contendo diferença d (ARIMA) que, apresenta como o principal caso contido nessa técnica. Segundo Ramser et al. (2015), eles apresentam conduta estacionária nos modelos AR(p) e MA(p), assim como a junção destes, o modelo ARMA (p,q).

O modelo ARIMA (p,d,q) é o efeito do uso de diferenciação na séries onde a média é variante, transformando-os estacionárias. Os modelos estacionários e os não estacionários, diferenciam-se pela quantidade de diferenças necessárias para estabilizar a série, simbolizado pela letra d (Marchezan & Souza, 2010).

2.3. Modelos fracionários

Os modelos ARIMA possibilitam também desenvolver séries temporais onde a diferença (d) pode apresentar valores não inteiros, chamados de fracionários (Lima, Góis & Ulises, 2007). Segundo Lopes, Macedo & Toyoshima (2016), essa é uma maneira de combinar bom comportamento de previsão da metodologia ARIMA (p,d,q) de curto prazo, com a perspectiva teórica de técnicas de memória longa, utilizando a flexibilidade do coeficiente de integração, originando assim em um modelo Autoregressivo Fracionário de Médias Móveis, conhecido como ARFIMA (p,d,q).

No modelo fracionário, de acordo com Hosking (1981), se espera que as autocorrelações sejam descritas de forma eficiente por meio da seleção dos parâmetros autoregressivos (p), assim como os de médias móveis (q), considerando o curto prazo. Por outro lado, segundo o autor, o comportamento em longo prazo deve ser bem caracterizado pelo parâmetro da diferença (d). Neste caso, o modelo ARFIMA pode ser descrito pela Equação (5), a seguir:

Quadro 1
Características do (d) fracionário

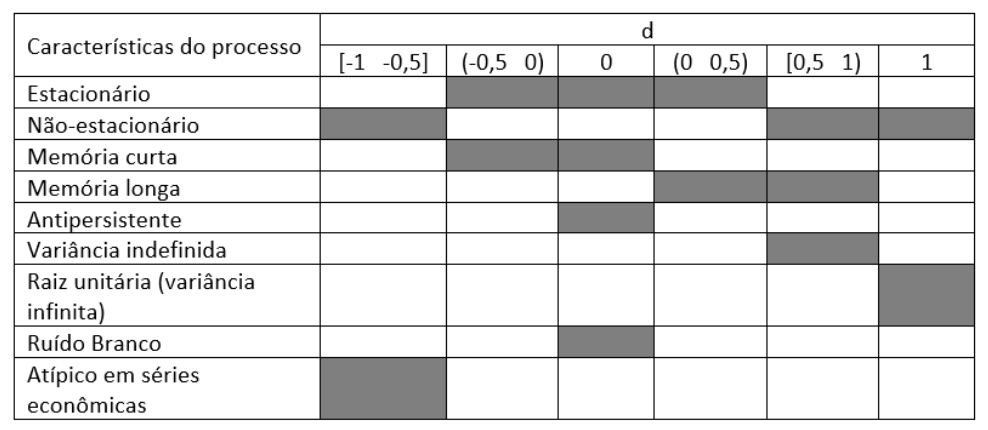
Fonte: Lima, Góis & Ulises (2007)

Nesse sentido, de acordo com estes autores, o processo é considerado de “memória-curta”, ou seja, se seus valores do presente apresentam pouca correlação com as observações passadas, quando a diferença fracionária (d) é maior do que -0,5 e menor ou igual a 0. Por outro lado, o processo pode ser dito de “memória-longa”, ou seja, se seus valores vigentes apresentarem grande correlação com o passado, quando (d) assumir valores maiores do que 0 e menores do que 0,5. O processo é considerado estacionário se a diferença fracionária (d) assumir valores maiores do que – 0,5 e menores do que 0,5, bem como caso (d) seja maior do que 0,5 e menor do que 1,0, se considera que a variância do processo é indefinida. Por fim, caso nenhuma dessas condições seja satisfeita, o processo é considerado não estacionário.

2.4. Modelos sazonais

Contudo, existem características particulares dos eventos estudados em séries temporais, o emprego de outros modelos é indispensável. Um desses eventos, segundo Souza (2016), é o acontecimento de periodicidade nos dados da série, demonstrando sazonalidade. Essa presença de periodicidade pode ser inserida nos modelos de Box e Jenkins por meio de um ARIMA sazonal, tornando possível também empregar diferenças nas séries sazonais para transformá-la em estacionária. Este quadro, segundo Werner & Ribeiro (2003), pode ser adicionada ao modelo SARIMA, pois este contempla os métodos que comportam séries definidas por autocorrelação sazonal. `

Entretanto, de acordo com Jacobs, Souza & Zanini (2016), no modelo SARIMA também existem limitações, onde que apenas um único modelo SARIMA não tem a aptidão de revelar todos os padrões encontrados na série. Em virtude disso, os autores aconselham utilizar o ciclo interativo de Box-Jenkins para a identificar o melhor modelo para a série de dados.

Neste tópico são descritas todas as etapas para a elaboração do estudo. A explicação de como a estimação foi realizada, é apresentada para facilitar a compreensão, tal como pode ser visto subsequentemente:

Passo 1 - Coleta dos Dados: nesta etapa foram coletados os dados mensais referentes às cotações da bolsa de valores de Chicago das culturas de soja, milho e trigo, retirados do site br.investing.com, no período de novembro de 2009 até abril de 2017, totalizando 90 meses.

Passo 2 - Identificação e Estimativa dos Modelos Concorrentes: inicialmente foi realizada a análise gráfica visando verificar a presença ou não de estacionaridade. O teste de raiz unitária Dickey-Fuller Aumentado (ADF) foi utilizado com o objetivo de confirmar ou não a hipótese de estacionaridade, nesta etapa também foi realizada a estimação e análise das funções de autocorrelação amostral (FAC) e parcial (FACP).

Passo 3 - Diagnóstico do Modelo ARIMA: verificou-se se o modelo estimado é adequado, com a característica de ruído branco, para tal comprovação foi utilizado o teste de hipótese de Ljung-Box. Os modelos que apresentaram essa característica foram denominados concorrentes e expostos em uma tabela com seus respectivos valores do Critério de Informação de Akaike (AIC) e o Critério de Informação Bayesiano de Schwarz (BIC), o modelo que apresentou o menor valor de BIC foi o escolhido. O AIC e o BIC levam em conta o número de parâmetros e a variância dos erros, privilegiando modelos mais parcimoniosos. Foram utilizados os melhores modelos e calculadas as estatísticas de previsão Erro Médio Absoluto Percentual (MAPE), Erro Quadrático Médio (MAE) e a estatística de U-Theil que verifica a qualidade do modelo em relação a uma previsão ingênua.

Passo 4 - Previsão: inicialmente foi descrita a função matemática do modelo adequado para cada uma das commodities. Com base nessa equação, foi realizada uma previsão para os próximos seis meses das cotações de soja, trigo e milho.

As etapas contendo o fluxograma de todo o processo de coleta dados até a previsão pode ser visualizada na Figura 1.

Figura 1
Fluxograma dos procedimentos metodológicos

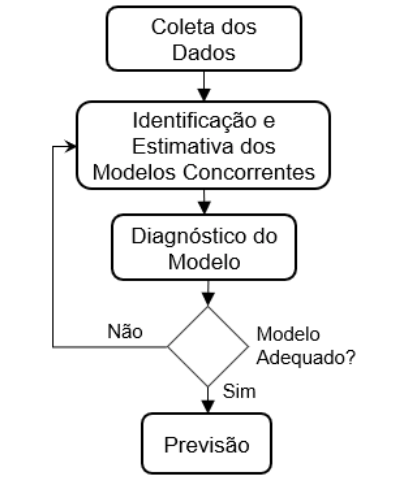
Fonte: Autores (2019)

Para a modelagem dos dados utilizou-se o software Eviews 9 S.V. Todas essas etapas são necessárias para atingir o objetivo do estudo.

A análise dos dados referentes à cotação do preço das culturas de soja, trigo e milho possibilitou entender o comportamento desses insumos ao longo do tempo na bolsa de valores. Em relação à soja, a análise gráfica dos dados mostrou uma elevação, em relação ao valor médio de ¢ US$ 1183,32/bushel (centavos de dólar/bushel), entre julho de 2010 até setembro de 2014, tendo seu ápice de preço em julho de 2012. O milho, por sua vez, apresentou valor médio de ¢ US$ 447,42/bushel, tendo seus maiores valores entre julho e agosto de 2012. Por outro lado, o trigo apresentou média de ¢ US$ 601,86/bushel, apresentando suas maiores cotações entre agosto de 2010 a maio de 2011, entre maio de 2011 e agosto de 2011 e maio de 2012 a fevereiro de 2013, conforme exposto na Figura 2.

Figura 2
Gráfico das cotações de soja, milho e trigo

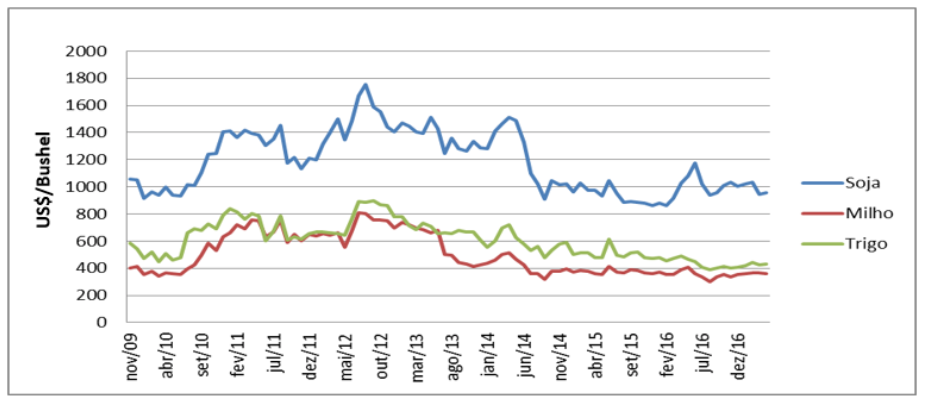
Fonte: Autores (2019)

Em sequência ao trabalho, o teste de raízes unitárias (ADF) foi utilizado para investigar em nível a presença de séries estacionárias para as três culturas, apresentando p-valor de 0,3040 para a soja, 0,1785 para o trigo e 0,4588 para o milho, indicando séries não estacionárias em nível, pois segundo Souza (2016) se considera como parâmetros a presença p-valores menores do que 5%. Todavia, a aplicação deste teste em primeira diferença apresentou p-valor de aproximadamente zero para os três tipos de grãos, indicando assim a presença de séries estacionárias em primeira diferença.

No entanto, levando em consideração a correlação sem nenhuma diferença entre os dados de cada cultura, por intermédio da Função de Autocorrelação (FAC) e pela Função de Autocorrelação Parcial (FACP), ambas as variedades apresentaram comportamento parecido. Nesse sentido, ambos os dados revelaram uma diminuição lenta da FAC e apenas um lag fora de controle (significativo) na FACP, demonstrando a presença de uma provável conduta autoregressiva das três séries, e também a incidência de períodos fracionários na série. Entretanto, os dados referentes à cotação de soja demonstraram comportamento adicional ao já citado, pois também evidenciaram inflexão no vigésimo segundo lag, podendo indicar também sazonalidade. 

Nesse sentido, de posse dessas conclusões foi possível estimar, por meio da metodologia ARIMA (p,d,q),  qual o melhor modelo de previsão para representar a série de cotação de cada cultura em questão. Assim, para as três séries foram estimadas modelos ARIMA, ARIMA com diferença sazonal, modelos SARIMA para verificar a presença de sazonalidade, assim como modelos ARFIMA para descobrir períodos fracionários nos dados. Logo, como resultado desse processo, foi possível identificar a presença de alguns modelos, assim como tabulá-los (Tabela 1) para posterior comparação e consequente escolha do melhor método para realiza previsão. 

Tabela 1
Modelos concorrentes da cotação de soja, trigo e milho

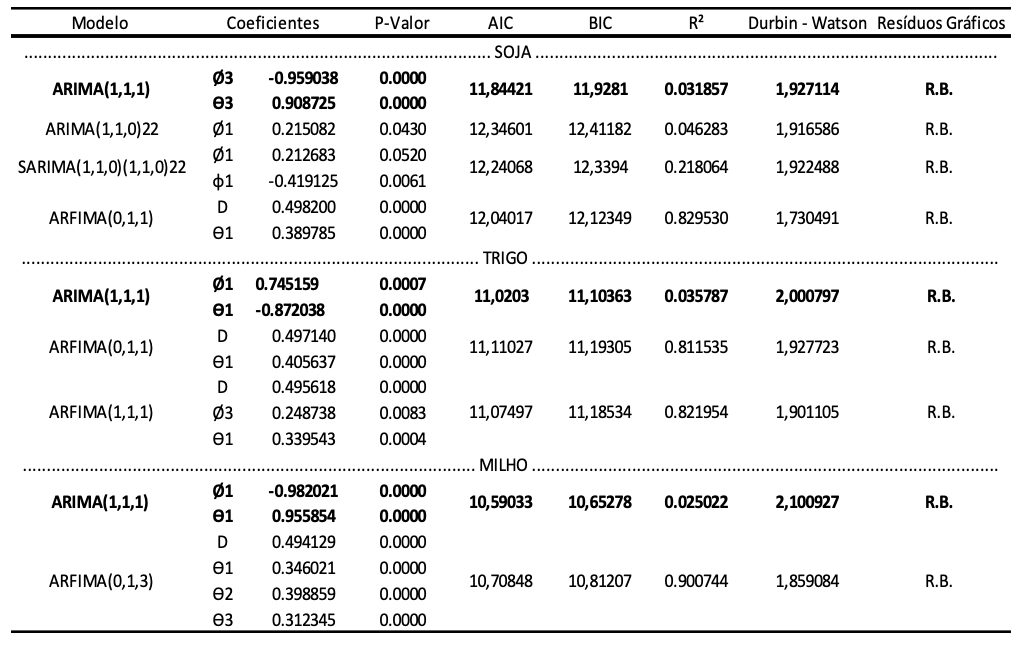
Fonte: Autores (2019)

Ao mesmo tempo, a tabela supracitada reuniu além dos modelos encontrados para cada série de cotação na bolsa, os valores dos coeficientes estimados, os seus p-valores respectivos, os valores de AIC, BIC e R² de cada método proposto, os valores do coeficiente de Durbin-Watson, assim como indicou a presença de média zero e variância constante para os resíduos de cada modelo, ou seja, a ocorrência de Ruído Branco (R.B).

Desse modo, foi possível comparar ambos os métodos concorrentes por meio dos menores valores de AIC e BIC, permitindo escolher o melhor modelo de previsão para cada cultura. Nesse sentido, o modelo mais apropriado, pelo método escolhido, para representar o comportamento da cotação das três culturas foi o modelo ARIMA (1,1,1). Esse modelo indica a necessidade de diferenciação da série para a ocorrência de estacionalidade, aponta a ocorrência de um componente autoregressivo de memória curta, pois o valor atual depende do valor anterior, assim como ele apresenta uma componente de médias móveis, demonstrando que o comportamento da cotação é explicado também por variáveis externas. 

Todavia, duas análises foram realizadas a fim de embasar tal proposição, um em relação aos erros de previsão e outra em relação ao comportamento visual gráfico do modelo. Assim, quanto a seus erros de previsão, utilizando para isso as metodologias de Erro Percentual Absoluto Médio (MAPE), Erro Absoluto Médio (MAE), Raiz do Erro Quadrático Médio (RMSE), assim como do Coeficiente de Desigualdade de Theil (Theil I.C.), exposto na Tabela 2.

Tabela 2
Erros de previsão de cada modelo

Fonte: Autores (2019)

Segundo a tabela supracitada, a escolha do modelo ARIMA (1,1,1) para as três cotações é pertinente, visto que apresentou os menores valores para ambos os casos. Para os três casos, os valores de RSME, MAE e THEIL I.C. apresentaram os menores valores, indicando que o modelo escolhido erra menos se comparado aos outros. Proposição ratificada pelos valores individuais do MAPE e THEIL I.C., pois indicam um erro de previsão de apenas 5,74% para a cotação de soja, 6,74% para o trigo e 7,29% para o milho de Erro Percentual Absoluto Médio, assim como ambas as cotações expõem valor de Coeficiente de Desigualdade de Theil próximos de zero, o recomendado pela literatura para bons modelos de previsão. Portanto, tais resultados justificam a escolha deste modelo como bom estimador para as séries em questão.  

Concomitantemente, a análise visual apresentou resultados convergentes a esta escolha. Conforme evidente na Figura 3, os gráficos dos valores previstos para cada cultura apresentaram comportamentos semelhantes aos gráficos das séries originais, de mesma maneira em todos os casos os valores estimados convergiram para o mesmo ponto final. Dessa forma, após tais resultados, foi possível confirmar com maior critério a escolha do modelo ARIMA (1,1,1) para estimar o comportamento futuro dessas séries, ou seja, realizar previsões. 

Figura 3
Análise visual da adequação do modelo proposto ao modelo real

Fonte: Autores (2019)

Posteriormente da escolha do modelo apropriado, foi possível descrevê-lo matematicamente, sendo as equações (7), (8) e (9) referentes às cotações de: soja, trigo e milho respectivamente, conforme evidenciado a seguir:

Dando sequência ao estudo, os resultados obtidos propiciaram a realização de previsão para a cotação por bushels de cada variedade analisada na bolsa, abrangendo um horizonte de 6 meses adiante, conforme evidenciado na Tabela 3, a seguir:

Tabela 3
Previsão para seis meses das cotações de soja, trigo e milho

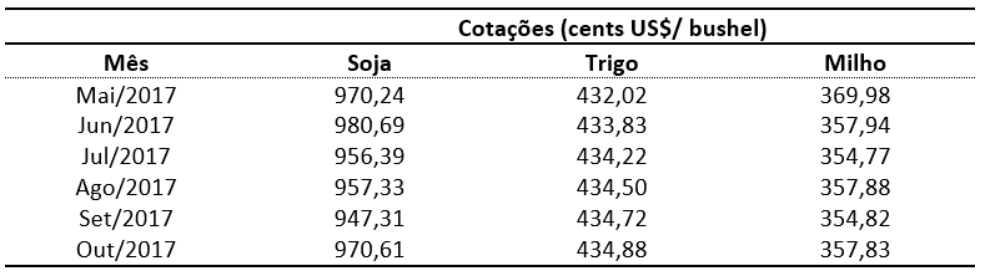
Fonte: Autores (2019)

Ao mesmo tempo, objetivando medir a acurácia desta previsão, as metodologias foram novamente utilizadas, abrangendo o cálculo do Erro Percentual Absoluto Médio (MAPE), Erro Absoluto Médio (MAE), bem como da Raiz do Erro Quadrático Médio (RMSE), conforme exposto na Tabela 4.

Tabela 4
Cálculo do erro de previsão

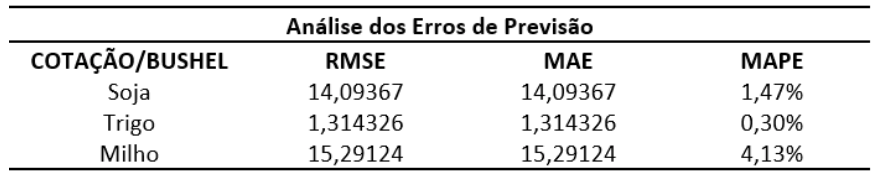
Fonte: Autores (2019)

Os cálculos referentes aos erros do modelo, compreendem valores para RSME e MAE menores do que 100, valores de MAPE inferiores a 10% e valores de UTheil bem próximo de zero, indicando a qualidade dos modelos de previsão.

Ao longo do estudo percebe-se que as três commodities tem uma evolução semelhante em seus preços, demonstrando variações significativas nos mesmos períodos, corroborando com o que foi apresentado por Caldarelli & Bacchi (2012), indicando que no aumento de preço de um produto, o mesmo pode ser substituído por outro, aumentando a demanda desse segundo e impulsionando também o seu preço. Ambas as três commodities apresentaram o mesmo modelo de previsão ARIMA (1,1,1), confirmando a semelhança entre a evolução histórica desses produtos.

De posse dos resultados expostos, é possível inferir a cotação futura das sacas de soja, trigo e milho no território nacional. Isto é possível por meio da conversão da cotação de bushel prevista para saca de cada mês, utilizando a cotação do dólar para o período desejado. Segundo esta lógica, vigente no mercado de valores, cada bushel equivale a centavos de Dólar, segundo a lógica de 1 Dolár/bushel. Ao mesmo tempo, em relação ao preço de saca basta saber a cotação atual do Dólar para encontrar o valor referência da saca, segundo a lógica: Dólar/Saca (Solluscapital, 2019). Desse modo, de posse dos valores atualizados desta moeda internacional, será possível estimar o valor cobrado por saca no país.

O presente estudo possibilitou ajustar um modelo de previsão para o preço de soja, trigo e milho por meio da metodologia Box & Jenkins, pode-se afirmar que o objetivo foi alcançado. O modelo que se destacou foi o ARIMA (1,1,1) para as três culturas. Salienta-se a semelhança histórica entre as variações nos preços dessas três commodities, induzindo a compreensão da relação de mercado entre elas. De posse destas informações é possível inferir o custo futuro da saca de cada uma das culturas analisadas, possibilitando assim melhor planejamento da compra, plantio e estocagem desses grãos.

Estas conclusões são baseadas nos testes realizados e na análise de resíduos. Ao considerar o teste U-Theil, pode-se afirmar que estes modelos são melhores do que os utilizados pelos métodos de previsão ingênua, pois apresentou resultado inferior a 1. Outro indicador que ratifica a eficiência deste modelo são os valores de MAPE para cada cultura, pois em todos os casos os modelos apresentaram erros entre 5,83% e 7,41%, valores relativamente baixos.

Este estudo apresentou três contribuições principais para a literatura. Primeiro, utilizou técnicas robustas de previsão aplicadas em commodities importantes para a balança comercial Brasileira. Segundo, demonstrou quantitativamente a forte relação de preços entre esses produtos agrícolas. Terceiro, comprovou a eficiência desses modelos de previsão por meio dos valores do MAPE.

Algumas limitações podem ser revistas em estudos futuros, como: (a) maior período de análise; (b) relacionar outras técnicas de previsão; (c) relacionar outros produtos agrícolas; e (d) relacionar a influência do cambia nos preços dos produtos agrícolas exportados. Esse estudo pode contribuir tanto para pesquisas acadêmicas sobre métodos quantitativos de previsão de produtos agrícolas, quanto para profissionais que trabalham diretamente com esses produtos e pretendem aumentar seus lucros.

Amaro, R. S. & Souza, A. M. (2014). Análise da Série de Retornos do Índice Bovespa utilizando como instrumental modelos Box-Jenkins. Espacios, 35(12).

Box, G. E., & Jenkins, G. M. (1976). Time series analysis: Forecasting and control San Francisco. Calif: Holden-Day.

Caldarelli, C. E., & Bacchi, M. R. P. (2012). Fatores de influência no preço do milho no Brasil. Nova economia, 22(1), 141-164.

Camponogara, A., Gallio, E., de Borba, W. F., & Georgin, J. (2015). O atual contexto da produção de trigo no Rio Grande do Sul. Revista Eletrônica em Gestão, Educação e Tecnologia Ambiental, 19(2), 246-257.

Dall'agnol, A., & Hirakuri, M. H. (2008). Realidade e perspectivas do Brasil na produção de alimentos e agroenergia, com ênfase na soja. Embrapa Soja. Circular técnica.

Fava, V. L. (2000). Manual de econometria. In: Vasconcelos, M. A. S.; Alves, D. São Paulo: Editora Atlas.

Fliehr, O. (2013). Analysis of transportation and logistics processes for soybeans in Brazil. Thünen Working Paper, 4, 1-107.

Haile, M. G., Kalkuhl, M., & Von Braun, J. (2015). Worldwide acreage and yield response to international price change and volatility: a dynamic panel data analysis for wheat, rice, corn, and soybeans. American Journal of Agricultural Economics, 98(1), 172-190.

Hikichi, S. E., Salgado, E. G., & Beijo, L. A. (2017). Forecasting number of ISO 14001 certifications in the Americas using ARIMA models. Journal of Cleaner Production, 147, 242-253.

Hosking, J. R. (1981). Fractional differencing. Biometrika, 68, 165–176.

Jacobs, W., Souza, A. M., & Zanini, R. R. (2016). Combination of Box-Jenkins and MLP/RNA models for forecasting. IEEE Latin America Transactions, 14(4), 1870-1878.

Jin, H. J., & Frechette, D. L. (2004). Fractional integration in agricultural futures price volatilities. American Journal of Agricultural Economics, 86(2), 432-443.

Junior, V. J. W. (2014). O mercado da soja no Brasil e na Argentina: semelhanças, diferenças e interconexões. Século XXI: Revista de Ciências Sociais, 4(1), 114-161.

Lima, R. C., Góis, M. R., & Ulises, C. (2007). Previsão de preços futuros de commodities agrícolas com diferenciações inteira e fracionária, e erros heteroscedásticos. Revista de Economia e Sociologia Rural, 45(3), 621-644.

Lopes, L. S., Macedo, L. R. D., & Toyoshima, S. H. (2016). Integração Fracionária nos Ciclos Econômicos de Longo Prazo no Brasil: Evidências Iniciais de Criticalidade Auto-Organizada. Revista Brasileira de Economia, 70(3), 315-335.

Makridakis, S., Wheelwright, S., & Hyndman, R. J. (1998). Forecasting: methods and applications. John Wiley & Sons.

Marchezan, A., & Souza, A. M. (2010). Forcasting the price of major grains produced in Rio Grande do Sul. Ciência Rural, 40(11), 2368-2374.

Martins, V. L. M., & Werner, L. (2014). Comparison of individual forecasts and their combinations: a study with industrial series. Production, 24(3), 618-627.

Moreira, R. R. (2014). Commodities prices volatility, expected inflation and GDP levels: an application for a net-exporting economy. Procedia economics and Finance, 14, 435-444.

Morettin, P. A., & Toloi, C. M. C. (1985). Previsão de séries temporais. São Paulo: Atual.

Oliveira, P. D., Nascente, A. S., Kluthcouski, J., & Portes, T. D. A. (2013). Crescimento e produtividade de milho em função da cultura antecessora. EMBRAPA, 43(3), 239-246.

Ramser, C. A. S., Souza, A. M., Mousquer, T. F., Moares, L. R., Santos, Clereci, A. V., A., Moraes, J. P. & Trindade, M. A. B. (2015). Previsão para o volume de vendas no varejo - Combustíveis e lubrificantes - no estado do Rio Grande do Sul. Espacios, 36(10).

Senna, V., Lima Junior, A. V., Menezes, F. R., Lírio, G. W. & Souza, A. M. (2014). Análise exploratória e aplicação da metodologia Box e Jenkins na modelagem e previsão de fluxo de caixa de empresa na área gráfica. Espacios, 35(10).

Silva, J., Ferreira, C., & Junior, S. (2004). Padrão sazonal de preços trigo: São Paulo, Paraná, Estados Unidos e Argentina. Informações Econômicas, 34(3).

Solluscapital. (2019). Tabela de Conversão. Recuperado em 10 novembro, 2019, de http://www.solluscapital.com.br/Portugues/tabela_de_conversao.html

Souza, F. M. (2006). Modelos Box & Jenkins aplicados a previsão de demanda de leitos hospitalares. Programa de Pós-Graduação em Estatística e Modelagem Quantitativa, Universidade Federal de Santa Maria (UFSM): Santa Maria, Brazil.

Souza, F. M. (2016). Modelos De Previsão: aplicações à energia elétrica - ARIMA- ARCH-AI e ACP. Curitiba: Appris.

Souza, F. M., Almeida, S. G. D., Guarnieri, J. P., Souza, A. M., & Lopes, L. F. D. (2010). Previsão do consumo de cimento no estado do Rio Grande do Sul. Pesquisa Operacional para o Desenvolvimento, 2(1).

Tseng, F. M., Yu, H. C., & Tzeng, G. H. (2002). Combining neural network model with seasonal time series ARIMA model. Technological forecasting and social change, 69(1), 71-87.

Werner, L., & Ribeiro, J. L. D. (2003). Previsão de demanda: uma aplicação dos modelos Box-Jenkins na área de assistência técnica de computadores pessoais. Gestão e produção, 10(1), 47-67.

1. Doutorando em Engenharia de Produção. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria (UFSM). cristiano.ziegler@bol.com.br

2. Mestre em Engenharia de Produção. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria (UFSM). antoniobrancov33@gmail.com  

3. Doutorando em Engenharia de Produção. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria (UFSM). renan.mitsuo@hotmail.com  

4. Estudante de graduação em Estatística. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria (UFSM). valentinawlirio@gmail.com

5. Estudante de graduação em Engenharia de Telecomunicações. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria (UFSM). tobiasdpf@gmail.com

6. Mestranda em Engenharia de Produção. Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa (UFSM). stefane.rodriguesufpa@gmail.com  

7. Professora do Departamento de Estatística (UFSM). Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria. rrzanini63@gmail.com

8. Professor do Departamento de Estatística (UFSM). Laboratório de Análise e Modelagem Estatística - LAME. Universidade Federal de Santa Maria. amsouza.sm@gmail.com