

Vol. 40 (Nº 18) Año 2019. Pág. 10
PAULE-VIANEZ, Jessica 1; COCA-PÉREZ, José L. 2 y GRANADO-SÁNCHEZ, Manuel 3
Recibido: 17/02/2019 • Aprobado: 03/05/2019 • Publicado 03/06/2019
3. Aplicación Distribución Libre de Mack y Bootstrap con Simulación
RESUMEN: En este trabajo estudiamos la cuantificación del riesgo de reserva en seguros no vida con Solvencia II, siendo una prioridad el establecimiento de un método que sea eficiente en sus estimaciones para disminuir el riesgo de insolvencia. Dentro de la metodología estocástica aplicada, analizamos la Distribución Libre de Mack y el método Bootstrap con Simulación, obteniendo que el método Bootstrap con Simulación utilizando el percentil 50 es el más adecuado para el establecimiento del riesgo de reserva. |
ABSTRACT: In this paper we study the quantification of reserve risk in non-life insurance with Solvency II, with a priority being the establishment of a method that is efficient in its estimates to reduce the risk of insolvency. Within the applied stochastic methodology, we analysed the Mack Free Distribution and the Bootstrap method with Simulation, obtaining that the Bootstrap method with Simulation using the 50th percentile is the most suitable for the establishment of reserve risk. |
Con la incorporación de la Directiva Europea Solvencia II en el marco regulador del sector asegurador, ha cobrado una gran importancia para las empresas de este sector la aplicación de metodologías acorde a esta normativa para la medición de los diferentes riesgos que pueden influir en la viabilidad de la empresa.
La normativa Solvencia II establece el cálculo del Capital de Solvencia Obligatorio cómo una medida que “permita a las empresas de seguros y reaseguros absorber pérdidas significativas y que ofrezca a los tomadores y beneficiarios de seguros una garantía razonable de que se efectuarán los pagos al vencimiento”(Directiva 2009/138/CE, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio -Solvencia II-). Esta normativa, al contrario de lo que ocurría hasta ahora, permite a las entidades realizar todas las operaciones que consideren oportunas, siendo ellas mismas las que deberán cuantificarse el capital necesario, bien utilizando la fórmula estándar derivada de esta normativa, o bien desarrollando un modelo propio que se adapte a los riesgos a los que se expone la empresa. Hay que tener en cuenta las correlaciones existentes entre los diferentes riesgos a los que se expone y se establecerá dicho Capital de Solvencia Obligatorio como “el valor en riesgo (VaR) de los fondos propios de la empresa con un nivel de confianza del 99,5% a un horizonte de un año” (Directiva 2009/138/CE, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio -Solvencia II-), siendo su valor igual a la diferencia entre la que considera la situación más desfavorable (el percentil 99,5) y la mejor estimación de las provisiones técnicas.
En este trabajo, la investigación se centra, dentro de todos los riesgos que operan en la actividad aseguradora y que deben incluirse en el cálculo del Capital de Solvencia Obligatorio, en el riesgo de suscripción, y dentro de este en el riesgo de reserva, estudiándolo sobre la modalidad de seguros no vida.
En este punto entra en juego el concepto de provisiones técnicas, el cual hace referencia “al importe que una empresa de seguros o de reaseguros tendría que pagar si transfiriera de manera inmediata todas sus obligaciones y derechos contractuales a otra entidad” (Directiva 2009/138/CE, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio -Solvencia II-). Solvencia II establece que “el valor de las provisiones técnicas será igual a la suma de la mejor estimación y de un margen de riesgo, siendo la mejor estimación”, comúnmente conocida como Best Estimate, “la media de los flujos de caja futuros ponderada por su probabilidad, teniendo en cuenta el valor temporal del dinero (valor actual esperado de los flujos de caja futuros) mediante la aplicación de la pertinente estructura temporal de tipos de interés sin riesgo”(Directiva 2009/138/CE, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio -Solvencia II-).
Existen diversos métodos para la obtención de dichas provisiones técnicas existiendo una clara diferenciación entre métodos deterministas y métodos estocásticos, sobre estos últimos serán sobre los que se centre este trabajo. Los métodos estocásticos permiten obtener una estimación de la incertidumbre ligada a los métodos deterministas mediante el uso de un modelo de probabilidad adecuado a la realidad que se desea medir (Albarrán y Alonso, 2010), es decir, permiten obtener un intervalo de confianza en las estimaciones futuras de pagos por siniestros.
Dentro de la metodología estocástica existen diversos métodos, destacando por su relevancia el método conocido cómo Distribución Libre de Mack (Mack, 1993), los modelos de regresión generalizados y el método basado en la técnica de remuestreo Bootstrap siguiendo la propuesta realizada por England (2002) en la que, a diferencia de la propuesta de England y Verrall (1999), esta pretende generar la distribución de la reserva estimada utilizando la distribución entera (Albarrán y Alonso, 2010).
El objetivo de esta investigación es determinar un método fiable y acorde a Solvencia II para la estimación de dichas provisiones técnicas en seguros no vida (sin incluir el margen de riesgo y sin tener en cuenta el valor temporal del dinero) y su desviación para la obtención del riesgo de reserva, el cual hace referencia al riesgo de que las provisiones técnicas establecidas por las pérdidas pasadas no sean suficientes para cubrir las reclamaciones por siniestros, es decir, es el riesgo de que las provisiones técnicas para pagos por siniestros ocurridos tengan que ser incrementadas en un período de doce meses (Munich Re, 2008).
En este trabajo se realiza una comparativa de los métodos Mack y Bootstrap, teniendo en cuenta la propuesta de England (2002) asumiendo una distribución Poisson con Sobredispersión para la segunda etapa del método. Para ello, la prueba empírica se realizará sobre una muestra real de una compañía aseguradora en su ramo de automóviles teniendo en cuenta los pagos por siniestros correspondientes a daños corporales. Para realizar dicha prueba utilizamos el programa estadístico R, siguiendo a Carrato et al. (2015).
A partir de este momento el trabajo se estructura cómo sigue:
En la Segunda Sección, explicamos el marco teórico en el que se describe los métodos utilizados para el cálculo del riesgo de reserva. En la Tercera Sección realizamos una prueba empírica con los dos métodos para la obtención del riesgo de reserva. En la Cuarta Sección analizamos los resultados obtenidos. Y, por último, en la Quinta Sección exponemos las conclusiones obtenidas.
Mack (1993) introdujo este modelo para obtener la desviación típica del método Chain Ladder. El método Chain Ladder se basa en la utilización de la información histórica de los pagos por siniestros para realizar una proyección futura de estos. Este método estructura los pagos por siniestros utilizando el triángulo de desarrollo de Taylor y Ashe (1983), el cuál organiza dichos pagos en función del año de ocurrencia de los siniestros y el momento de los pagos de estos.
El método Chain Ladder, cómo método determinista que es, no permite la estimación del error de predicción surgiendo por tanto en este punto diversas alternativas para estimar dicho error. Una de las alternativas más conocidas ha sido La Distribución Libre de Mack, que fue la primera propuesta para establecer el error de predicción del Chain Ladder, aunque sólo tiene en cuenta los dos primeros momentos (Wüthrich, 2008).
Mack demostró que las estimaciones del Chain Ladder de pagos por siniestros acumulados son insesgados, no obstante, hay muchos otros estimadores que cumplen esta condición (Schmidt, 1997). El método propuesto por Mack se basa en la obtención del error cuadrático medio de la reserva, no obstante, presenta como principal limitación la imposibilidad de aplicar este método cuando la estimación de pagos por siniestros en un año de desarrollo es inferior a la estimación de pagos por siniestros en el año de desarrollo anterior, es decir, cuando existen cobros por siniestros por parte de la entidad aseguradora superando estos a los pagos en un mismo año.
Los pasos para aplicar el método propuesto por Mack son los siguientes:

La metodología Bootstrap fue iniciada por Efron (1976) e introducida en la estimación del riesgo de reserva de compañías aseguradoras por Lowe (1994). Entre otros, esta metodología fue utilizada por England y Verrall (1999) quienes proponen un método de estimación del riesgo de reserva con Bootstrap como una forma fácil de obtener el riesgo de reserva, el cual, al igual que el método Mack, utiliza como metodología base el método Chain Ladder.
El modelo propuesto por England y Verrall (1999) utiliza además lo realizado por Renshaw y Verrall (1998), quienes propusieron la utilización del modelo lineal generalizado Poisson-Sobredisperso para poder realizar un tratamiento estocástico del método Chain Ladder, coincidiendo la estimación de las reservas del modelo lineal generalizado con la estimación realizada con el Chain Ladder. La propuesta de England y Verrall (1999) se basa en la utilización de dicho modelo para la obtención de la estimación de reservas y su varianza una vez obtenido un nuevo triángulo utilizando los residuales de Pearson remuestreados para obtener el error de predicción, proceso que repite N veces.
Sobre la propuesta que realizaron England y Verrall (1999) de la metodología Bootstrap en la estimación del riesgo de reserva, England (2002) introduce cambios sobre esta, frente a la estimación de los dos primeros momentos que realizaban England y Verrall (1999). England (2002) introduce un modelo dividido en dos etapas: Bootstrapping para obtener el error de estimación y simulación para obtener el error de proceso, lo que nos permite obtener en cada muestreo la distribución de predicción, en lugar de sólo los dos primeros momentos (England, 2002).
Los pasos para aplicar el método Bootstrap propuesto por England (2002) se divide en las dos etapas que describe el método.


Se procede a aplicar ambas metodologías sobre los pagos por siniestros registrados en el periodo 2005-2014 en el área correspondiente a los daños corporales en seguros de automóviles, los cuáles se disponen en el triángulo de desarrollo de Taylor y Ashe (1983) (Tabla 1).
Tabla 1
Triángulo de pagos por
siniestros original acumulado
Años origen |
Años Desarrollo |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2005 |
11.235.371 |
19.153.350 |
22.937.311 |
24.667.612 |
25.350.647 |
26.707.136 |
26.965.114 |
27.060.103 |
27.147.861 |
27.997.375 |
2006 |
3.270.400 |
7.163.177 |
8.124.207 |
8.393.798 |
8.720.362 |
9.007.158 |
9.162.003 |
9.175.910 |
9.341.923 |
|
2007 |
3519.475 |
7.496.147 |
8.437.066 |
9.082.182 |
9.590.659 |
9.666.939 |
9.441.871 |
9.416.776 |
|
|
2008 |
3.381.472 |
6.065.014 |
7.167.855 |
7.814.002 |
8.063.243 |
8.334.413 |
9.034.876 |
|
|
|
2009 |
3.523.292 |
6.669.596 |
8.021.433 |
8.471.042 |
9.111.275 |
9.355.833 |
|
|
|
|
2010 |
4.042.719 |
6.808.154 |
7.654.718 |
8.059.487 |
8.249.464 |
|
|
|
|
|
2011 |
3.608.421 |
6.414.563 |
7.525.221 |
7.691.767 |
|
|
|
|
|
|
2012 |
3.315.770 |
5.714.896 |
6.458.483 |
|
|
|
|
|
|
|
2013 |
3.281.802 |
5.915.518 |
|
|
|
|
|
|
|
|
2014 |
3.547.580 |
|
|
|
|
|
|
|
|
|
Sobre este triángulo se obtienen los factores de desarrollo aplicando el Chain Ladder, los cuáles utilizamos en ambos métodos (Tabla 2).
Tabla 2
Factores de desarrollo
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Rj |
1,822428 |
1,165556 |
1,061718 |
1,039743 |
1,016536 |
1,001839 |
1,007003 |
1,031292 |
Una vez obtenidos los factores de desarrollo obtenemos las estimaciones de pagos por siniestros ocurridos, pero no notificados como la diferencia entre los pagos acumulados en el último año de desarrollo y los pagos registrados, los cuales hacen referencia a las estimaciones de reservas para el método Mack (Tabla 3).
Tabla 3
Estimaciones de pagos por siniestros obtenidas aplicando el Chain Ladder
Años origen |
Años Desarrollo |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2005 |
11.235.371 |
19.153.350 |
22.937.311 |
24.667.612 |
25.350.647 |
26.707.136 |
26.965.114 |
27.060.103 |
27.147.861 |
27.997.375 |
2006 |
3.270.400 |
7.163.177 |
8.124.207 |
8.393.798 |
8.720.362 |
9.007.158 |
9.162.003 |
9.175.910 |
9.341.923 |
9.634.252 |
2007 |
3519.475 |
7.496.147 |
8.437.066 |
9.082.182 |
9.590.659 |
9.666.939 |
9.441.871 |
9.416.776 |
9.482.724 |
9.779.459 |
2008 |
3.381.472 |
6.065.014 |
7.167.855 |
7.814.002 |
8.063.243 |
8.334.413 |
9.034.876 |
9.051.491 |
9.114.881 |
9.400.105 |
2009 |
3.523.292 |
6.669.596 |
8.021.433 |
8.471.042 |
9.111.275 |
9.355.833 |
9.510.537 |
9.528.027 |
9.594.754 |
9.894.994 |
2010 |
4.042.719 |
6.808.154 |
7.654.718 |
8.059.487 |
8.249.464 |
8.552.573 |
8.693.994 |
8.709.982 |
8.770.981 |
9.045.443 |
2011 |
3.608.421 |
6.414.563 |
7.525.221 |
7.691.767 |
7.992.265 |
8.285.924 |
8.422.936 |
8.438.426 |
8.497.522 |
8.763.428 |
2012 |
3.315.770 |
5.714.896 |
6.458.483 |
6.857.086 |
7.124.975 |
7.386.767 |
7.508.911 |
7.522.720 |
7.575.403 |
7.812.454 |
2013 |
3.281.802 |
5.915.518 |
6.894.866 |
7.320.401 |
7.606.391 |
7.885.871 |
8.016.268 |
8.031.010 |
8.087.253 |
8.340.321 |
2014 |
3.547.580 |
6.465.210 |
7.535.563 |
8.000.640 |
8.313.206 |
8.618.656 |
8.761.70 |
8.777.282 |
8.838.752 |
9.115.335 |
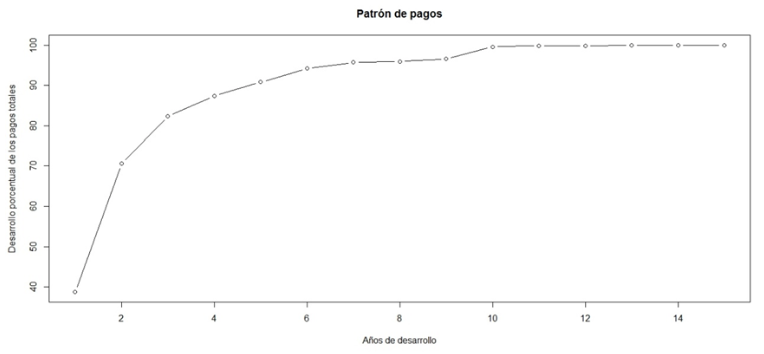
Podemos observar la evolución de los pagos por siniestros en el patrón de pagos (Gráfico 1). Se puede observar cómo sobre el 7º año de desarrollo se produce un estancamiento en los pagos por siniestros debido a que en estos años en algunos casos se han producido unos mayores cobros por siniestros que pagos por estos por parte de la compañía, produciéndose de nuevo el crecimiento a partir del 9º año de desarrollo.
Gráfico 1
Patrón de pagos en función del año de notificación de los siniestros
En la Tabla 4 se reportan los datos obtenidos para la estimación del riesgo de reserva aplicando la propuesta de Mack.
Analizando los datos desagregados en función del año de ocurrencia de los siniestros nos encontramos con un gran incremento de las previsiones de pago por siniestros ocurridos en el año 2014 frente a sus previsiones futuras respecto al resto de años, lo cual podemos interpretar como un mayor riesgo de variaciones en las estimaciones de pagos futuros frente al resto de años estudiados. Esto lo podemos confirmar observando el error obtenido con dicha metodología el cual, en términos absolutos, prácticamente duplica al del año anterior. En cambio, si observamos el peso que el riesgo tiene sobre los pagos por siniestros ocurridos, pero no notificados, observamos como el mayor peso lo encontramos en los años centrales, destacando el error frente a la estimación del año 2009, en el que el error representa un 90,7% de la estimación, provocando un amplio intervalo de resultados posibles.
Tabla 4
Datos obtenidos aplicando la distribución libre de Mack por año de ocurrencia
|
Pagos registrados |
Desarrollo actual |
Pagos acumulados |
IBNR |
Error Mack |
CV (IBNR) |
2005 |
27.997.375 |
1,00 |
27.997.375 |
0 |
0 |
NaN |
2006 |
9.341.923 |
0,970 |
9.634.252 |
292.329 |
41.043 |
0,140 |
2007 |
9.416.776 |
0,963 |
9.779.459 |
362.683 |
144.158 |
0,397 |
2008 |
9.034.876 |
0,961 |
9.400.105 |
365.229 |
146.214 |
0,400 |
2009 |
9.355.833 |
0,946 |
9.894.994 |
539.161 |
488.954 |
0,907 |
2010 |
8.249.464 |
0,912 |
9.045.443 |
795.979 |
507.971 |
0,638 |
2011 |
7.691.767 |
0,878 |
8.763.428 |
1.071.661 |
537.574 |
0,502 |
2012 |
6.458.483 |
0,827 |
7.812.454 |
1.353.971 |
549.182 |
0,406 |
2013 |
5.915.518 |
0,709 |
8.340.321 |
2.424.803 |
645.708 |
0,266 |
2014 |
3.547.580 |
0,389 |
9.115.335 |
5.567.755 |
1.220.124 |
0,219 |
En la Tabla 5 se recoge la estimación de reservas y su riesgo total para el periodo estudiado.
Se observa cómo los pagos realizados hasta el momento representan un 88% respecto a la estimación de pagos totales, resultando una estimación de pagos por siniestros ocurridos, pero no notificados de 12.773.571 u.m. con un riesgo de 2.052.019 u.m. representando este un 16% respecto a la estimación.
Tabla 5
Datos obtenidos aplicando la
distribución libre de Mack. Totales
|
Totales |
Pagos registrados |
97.009.595 |
Desarrollo actual |
0,88 |
Pagos estimados |
109.783.166 |
IBNR |
12.773.571 |
Error Mack |
2.052.019 |
CV (IBNR) |
0,16 |
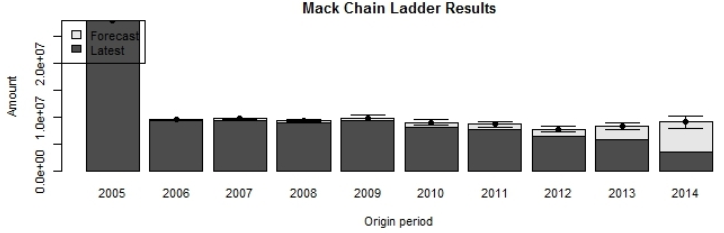
En el Gráfico 2 se muestran los pagos por siniestros actuales, la estimación futura y su variabilidad, en la que destaca la dispersión que se produce en los siniestros ocurridos en 2009.
Gráfico 2
Gráfico de resultados aplicando
la distribución libre de Mack
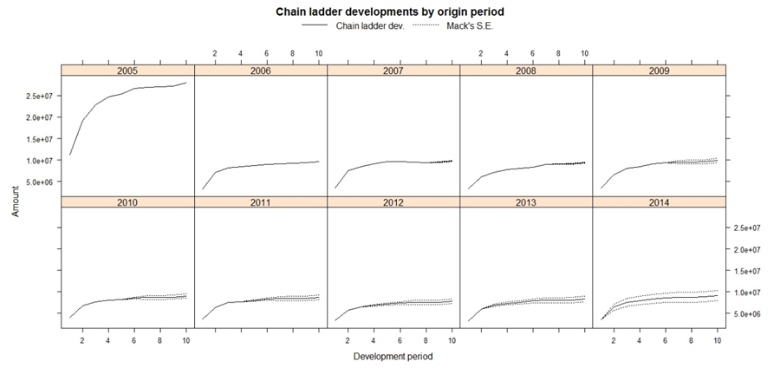
Si se desagregan los resultados en función de la ocurrencia de los siniestros, se puede observar la posible variabilidad de estos en el Gráfico 3. Así, a siniestros más cercanos mayor variabilidad en los posibles pagos, produciéndose un mayor incremento a partir de 2009.
Gráfico 3
Variación de pagos por siniestros por año de
ocurrencia aplicando la distribución libre de Mack
Una vez analizados los datos obtenidos con el modelo Mack, se procede a obtener los resultados aplicando el modelo Bootstrap con Simulación (Tabla 5). Se remuestrea 10.000 veces para obtener una mayor fiabilidad en los datos.
Tabla 6
Resultados obtenidos aplicando el método Bootstrap
con Simulación por años de ocurrencia
|
Pagos registrados |
Pagos estimados |
Media IBNR |
Error IBNR |
IBNR 50% |
IBNR 75% |
IBNR 95% |
IBNR 99% |
IBNR 99,5% |
2005 |
27.997.375 |
27.997.375 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2006 |
9.341.923 |
9.636.714 |
294.791 |
265.941 |
277.644 |
411.462 |
804.150 |
1.202.987 |
1.437.444 |
2007 |
9.416.776 |
9.779.961 |
363.185 |
289.897 |
297.326 |
502.311 |
922.817 |
1.301.095 |
1.443.858 |
2008 |
9.034.876 |
9.400.177 |
365.301 |
290.130 |
302.522 |
503.535 |
926.085 |
1.329.609 |
1.487.535 |
2009 |
9.355.833 |
9.896.568 |
540.735 |
358.352 |
471.449 |
725.300 |
1.219.195 |
1.680.524 |
1.904.090 |
2010 |
8.249.464 |
9.048.856 |
799.393 |
425.628 |
729.276 |
1.039.956 |
1.604.981 |
2.068.479 |
2.246.495 |
2011 |
7.691.767 |
8.765.003 |
1.073.236 |
486.390 |
1.004.183 |
1.353.004 |
1.958.457 |
2.516.500 |
2.727.679 |
2012 |
6.458.483 |
7.811.546 |
1.353.063 |
554.601 |
1.283.491 |
1.682.849 |
2.355.819 |
2.915.068 |
3.147.240 |
2013 |
5.915.518 |
8.338.648 |
2.423.130 |
805.859 |
2.325.526 |
2.898.896 |
3.885.114 |
4.656.088 |
5.041.464 |
2014 |
3.547.580 |
9.142.667 |
5.595.087 |
1.627.013 |
5.434.761 |
6.471.347 |
8.378.543 |
10.891.259 |
11.889.010 |
Este método permite obtener una función de distribución de las estimaciones al contrario de lo que ocurre con la Distribución Libre de Mack, con la que sólo se puede obtener la estimación de las reservas y su error. Aplicar este modelo nos permite decantarnos por diferentes estadísticos para obtener las estimaciones de reservas. Los datos globales obtenidos aplicando esta metodología se observan en la Tabla 7.
En base a los datos se observa cómo la media y la mediana tienen valores muy similares, por lo que se puede determinar que la función de distribución es bastante simétrica. Si se analiza el coeficiente variación de la media se puede observar cómo este es igual a 0,19.
Tabla 7
Resultados obtenidos aplicando el método
Bootstrap con Simulación. Totales
|
Totales |
Pagos registrados |
97.009.595 |
Pagos estimados |
109.817.514 |
Media IBNR |
12.807.919 |
Error IBNR |
2.490.333 |
IBNR 50% |
12.598.533 |
IBNR 75% |
14.282.984 |
IBNR 95% |
17.144.642 |
IBNR 99% |
19.953.847 |
IBNR 99,5% |
21.030.986 |
Los datos anteriores se pueden observar gráficamente en la función de distribución de los siniestros ocurridos, pero no notificados (Gráfico 4).
Resulta interesante observar la gran dispersión de valores posibles que refleja la función de distribución Bootstrap, lo cual incide en una mayor incertidumbre en el resultado final de pagos.
Gráfico 4
Función de distribución de los siniestros ocurridos, pero no
notificados obtenida aplicando Bootstrap con Simulación

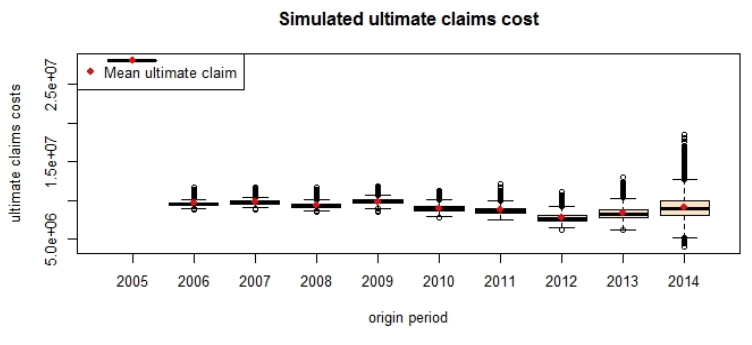
El Gráfico 5 muestra el boxplot de los pagos por siniestros totales estimados destacando el gran decremento en el nivel de pagos a partir de 2005. Se observa como la media y la mediana son muy similares por lo que la distribución se aproxima a una normal. Hay que tener en cuenta que también existen bastantes valores atípicos en las estimaciones realizadas.
Gráfico 5
Diagrama de caja del total de pagos por
siniestros aplicando Bootstrap con Simulación
Analizando los resultados de estimaciones obtenidas con el método Mack (1993) y el método Bootstrap con Simulación (England, 2002) (Tabla 8), se observa como las estimaciones de pagos por siniestros ocurridos pero no notificados obtenidos con ambos métodos son muy similares, y a la vez estas son muy similares a la estimación obtenida con el percentil 50 utilizando el Bootstrap con Simulación, alejándose considerablemente las estimaciones para los distintos percentiles analizados por lo que hemos descartado los percentiles 99 y 99,5.
Tabla 8
Estimación de pagos por siniestros ocurridos, pero no notificados
utilizando la distribución libre de Mack y el Bootstrap con Simulación
|
Distribución Libre de Mack |
Bootstrap con Simulación |
|||
Media |
Percentil 50 |
Percentil 75 |
Percentil 95 |
||
IBNR |
12.773.571 |
12.807.919 |
12.598.533 |
14.282.984 |
17.144.642 |
Si analizamos los errores obtenidos con ambos métodos (Tabla 9), el error obtenido utilizando la Distribución Libre de Mack ha sido inferior al cometido con Bootstrap con Simulación, al igual que dichos errores respecto a la media.
Tabla 9
Error en los pagos por siniestros ocurridos, pero no notificados
utilizando la distribución libre de Mack y el Bootstrap con Simulación
|
Distribución Libre de Mack |
Bootstrap con Simulación |
Error |
2.052.019 |
2.490.333 |
CV (IBNR) |
0,16 |
0,19 |
En base a las estimaciones realizadas, los dos métodos presentan resultados muy similares, presentando una mayor variación del riesgo respecto a la estimación media la aplicación del Bootstrap con Simulación, por tanto, podemos determinar que los resultados obtenidos con ambos métodos son viables. No obstante, analizando la realidad, los recobros por parte de una compañía aseguradora suelen darse en más ocasiones de las analizadas provocando la obtención de los factores de desarrollo del Chain Ladder inferiores a 1, lo que imposibilita la aplicación del modelo de Mack.
Respecto a la estimación realizada para las reservas con el método Bootstrap con Simulación cabe mencionar cómo utilización para la constitución de las provisiones técnicas otros estadísticos diferentes a la media, cómo podría ser el percentil 50, que cómo se ha observado, es bastante similar al obtenido para la media.
En base al análisis realizado, se puede determinar que ambos métodos son adecuados para la estimación de las provisiones técnicas y el riesgo de reserva, siempre que los recobros no supongan un crecimiento negativo entre los pagos realizados en un año de desarrollo frente al siguiente, lo que provoca que la Distribución Libre de Mack no se pueda aplicar.
Respecto al método Bootstrap con Simulación propuesto por England (2002), este método además de permitir trabajar en todos los escenarios posibles permite establecer una función de distribución con los resultados obtenidos. Esto posibilita el establecimiento de otras unidades de medida para la constitución de las provisiones técnicas cómo puede ser el percentil 50, el cuál cómo se observa, no presenta muchas diferencias respecto a la media y otorga un menor peso a los valores extremos, los cuales, en muchas ocasiones, son prácticamente imposibles de realizarse. Por tanto, en base a los resultados obtenidos, el mejor método, en términos generales para establecer los pagos por siniestros ocurridos, pero no notificados, es el método Bootstrap propuesto por England (2002), siendo el estadístico más adecuado para establecer dichas estimaciones el percentil 50.
Albarrán Lozano, I., & Alonso González, P. (2010). Métodos Estocásticos de Estimación de las Provisiones Técnicas en el marco de Solvencia II. Cuadernos de la Fundación MAPFRE, (158), Madrid: Fundación Mapfre.
Carrato, A., Concina, F., Gesmann, M., Murphy, D., Wüthrich, M., & Zhang, W. (2015). Claims reserving with R: ChainLadder- 0. 2. 2. Package Vignette. R-project. Disponible en: https://cran.rproject.org/web/packages/ChainLadder/vignettes/ChainLadder.pdf [Revisado: 17-02-2019].
Efron, B. (1992). Bootstrap methods: another look at the jackknife. In Breakthroughs in statistics (pp. 569-593). Springer, New York, NY.
England, P. (2002). Addendum to “Analytic and bootstrap estimates of prediction errors in claims reserving”. Insurance: Mathematics and Economics, 31 (3), 461-466.
England, P. D., & Verrall, R. J. (2002). Stochastic claims reserving in general insurance. British Actuarial Journal, 8(3), 443-518.
England, P., & Verrall, R. (1999). Analytic and bootstrap estimates of prediction errors in claims reserving. Insurance: mathematics and economics, 25(3), 281-293.
Lowe, J. (1994). A practical guide to measuring reserve variability using: Bootstrapping, Operational Time and a distribution free approach. Proceeding of the 1994 General Insurance Convention, Institute of Actuaries and Faculty of Actuaries.
Mack, T. (1993). Distribution-free calculation of the standard error of chain ladder reserve estimates. Astin bulletin, 23(2), 213-225.
Mack, T. (1994a). Which stochastic model is underlying the chain ladder method?. Insurance: mathematics and economics, 15(2-3), 133-138.
Mack, T. (1994b). Measuring the variability of chain ladder reserve estimates. In Casualty Actuarial Society Forum (Vol. 1, No. 1, pp. 101-83). Edward W. Frees, Richard A. Derrig and Glenn Meyers Excerpt More information.
Munich Re. (2008). Solvency II for property-casualty insurers (I) Technical provisions and capital requirement for the underwriting Risk. Münchener Rück, Munich Re Group.
Parlamento Europeo y Consejo de la Unión Europea., 2009. Directiva 2009/138/CE, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio (Solvencia II).
Renshaw, A. E., & Verrall, R. J. (1998). A stochastic model underlying the chain-ladder technique. British Actuarial Journal, 4(4), 903-923.
Schmidt, K. D. (1997). Non-optimal prediction by the chain ladder method. Insurance: Mathematics and Economics, 21(1), 17-24.
Taylor, G. C., & Ashe, F. R. (1983). Second moments of estimates of outstanding claims. Journal of Econometrics, 23(1), 37-61.
Wüthrich, M.V. (2008). Prediction error in the chain Ladder method.Insurance: Mathematics and Economics, 42(1), 378-388.
1. Profesora e investigadora en el Departamento de Economía de la Empresa, Universidad Rey Juan Carlos, España. Email: jessica.paule@urjc.es
2. Profesor titular y Doctor en el Departamento de Economía Financiera y Contabilidad, Universidad de Extremadura, España. Email: jlcoca@unex.es
3. Profesor colaborador en el Departamento de Economía Financiera y Contabilidad, Universidad de Extremadura, España. Email: m_granado@unex.es