

 Vol. 40 (Number 15) Year 2019. Page 24
Vol. 40 (Number 15) Year 2019. Page 24
OREJUELA, Juan Pablo 1 y HERNÁNDEZ, German Jairo 2
Received: 23/01/2019 • Approved: 10/04/2019 • Published 06/05/2019
ABSTRACT: The school bus routing problem has been known to be a sensitive issue; furthermore, in the current context in which the population is concentrated in urban areas and traffic becomes an element that adds complexity to the problem. It is specifically hard when the travel time, from node to node, changes depending on the start time of the travel. In that sense the paper presents this component, known as time dependent, is introduced into the school bus routing problem. |
RESUMEN: El problema de ruteo de buses escolares es un tema sensible en el contexto actual, en el que la población se concentra en áreas urbanas y el tráfico se convierte en un elemento que le agrega complejidad. Especialmente cuando el tiempo de viaje, de nodo a nodo, cambia según la hora de inicio del viaje. En este documento se presenta este componente, conocido como dependiente del tiempo, el cual se introduce en el problema del ruteo de buses escolares. |
The School Bus Routing Problem, (SBRP), has been widely studied since it was proposed in the literature (R M Newton & Thomas, 1969). The SBRP in general has as goal to plan an effective schedule for a fleet of school buses, in which each bus picks up students from several stops and then drives them at school; the situation is the same in the return route, from the school to their homes (J Park, Tae, & Kim, 2010).
In the planning of school routes, several needs and restrictions must be considered like: minimization of a child's time in the transportation system, maximum bus capacity, and time windows for the arrival to the school and minimization of the total distance traveled. All previous, generates a complex problem that has attracted the attention of a significant number of researchers (Kinable, Spieksma, & Vanden Berghe, 2014).
The SBRP is part of the family of the vehicle routing problem, (VRP, Vehicle Routing Problem) (X. Chen, Kong, Dang, Hou, & Ye, 2015b) and is composed of three main sub-problems: a) The allocation of stops to the buses; b) The assignment of students to buses c) the route selection of each bus. These types of problems are of type NP-Hard. (J Park et al., 2010), (Kinable et al., 2014), (Fügenschuh & Martin, 2006), (Rocha, González, & Orjuela, 2011).
On the other hand, the growth of urban areas has caused the quality of life to be affected by congestion in traffic. Likewise, cities become less competitive because of increases in travel times, fuel consumption, atmospheric pollution and the operating costs of the fleets.
School transport is part of this mobility problem, although it is only one of the components it is directly affected by the same factors. The transportation of students to schools and colleges is one of the generators of a large amount of morning traffic and generally during peak hours; the school transportations users are composed from on one hand, the parents who decide to take their children to school, sometimes sharing a vehicle with some neighboring children, and on the other hand, the school buses that provide this special transportation service.
Table 1
Review of literature on SBRP
Reference |
Time |
Mixed Load |
Multi-objective |
Social |
Environmental |
Economic |
(Braca, Bramel, Posner, & Simchi-Levi, 1997) |
No |
Yes |
No |
No |
No |
Yes |
(M Spada, Bierlaire, & Liebling, 2005) |
No |
Yes |
No |
Yes |
No |
No |
(Junhyuk Park & Kim, 2010) |
No |
Yes |
No |
No |
No |
No |
(Junhyuk Park, Tae, & Kim, 2012a) |
No |
Yes |
No |
No |
No |
Yes |
(Schittekat et al., 2013) |
No |
Yes |
No |
No |
No |
Yes |
(Bögl, Doerner, & Parragh, 2015) |
No |
Yes |
No |
No |
No |
Yes |
(Ellegood, Campbell, & North, 2015) |
No |
Yes |
No |
No |
No |
Yes |
(X. b Chen et al., 2015) |
No |
Yes |
Yes |
No |
No |
Yes |
(Kang, Kim, Felan, Choi, & Cho, 2015) |
No |
Yes |
No |
No |
No |
Yes |
(Silva, Sarubbi, Silva, Porto, & Nunes, 2015) |
No |
No |
No |
No |
No |
Yes |
(Souza Lima et al., 2016) |
No |
Yes |
No |
No |
No |
Yes |
Several authors have raised the importance of involving the effects of traffic on routing problems (Sankaran & Wood, 2007; Ziliaskopoulos & Waller, 2000) and various applications have been developed in that direction (Afshar-Nadjafi & Afshar-Nadjafi, 2014; Z Duan, Sun, Sun, & Li, 2015; Ehmke, Campbell, & Thomas, 2016; Setak, Habibi, Karimi, & Abedzadeh, 2015; Soysal, Bloemhof-Ruwaard, & Bektas, 2015; Wen & Eglese, 2015; Zare-Reisabadi & Mirmohammadi, 2015). Specifically in the SBRP, (Levin & Boyles, 2016) recognized its complexity by addressing the effect of peak and off-peak hours.
Two approaches have been developed to address the school bus routing problem (M Spada, Bierlaire, & Liebling, 2005): the focus of the home and the focus of the school. In the first, mixed loading is allowed; that is, children from different schools can be picked up at the same time by a route (Junhyuk Park, Tae, & Kim, 2012b). Conversely, in the school approach mixed loading is not allowed. The last one is the problem most addressed in the literature from the perspective of the so-called Capacitated VRP (X. Chen, Kong, Dang, Hou, & Ye, 2015a; Desrosiers, Ferland, Rousseau, Lapalme, & Chapleau, 1981). This approach, in addition, considers the time de-pendent as a differential factor in the analysis.
Although it is true in the literature, different researches have been raised about the time dependent CVRP, in the specific case of school bus routing, no concrete applications have been identified. As seen in the table 1.
In (J Park et al., 2010) a generic decomposition structure of the SBRP is presented. This decomposition of the SBRP is proposed in order to divide a big problem into small sub-problems which can be solved separately, facilitating the solution of the global problem.
Although the proposed decomposition is an aid for the solution of the school bus routing problem, it cannot always be carried out, because every vehicle routing problem has its own elements that make it difficult to characterize. According to the re-search carried out by Park et al. (J Park et al., 2010), in most of the literature they only consider some sub-problems and those are treated separately due to their complexity and size. How-ever, it is still an indispensable tool to divide the problem and solve it step by step. The five sub-problems of the SBRP are: data preparation, selection of bus stops, generation of routes, adjustment with the school bell and bus programming.
Data preparation. The objective of solving this sub-problem is to characterize it and prepare the data in such a way that it can be used to solve the following sub-problems, where the main deliverable of this part is the characterization of the nodes (students and school) and the matrix of distances between them.
Characterization of the SBRP. For the selection of the different solution techniques and the different ways to approach the SBRP problem it is important to define the main characteristics that are decisive for the roads to be taken. Throughout the development of the SBRP, 8 main criteria have been highlighted, which were proposed by J Park et al., (J Park et al., 2010).
Distance matrix: The main deliverable of this sub-problem is the distance matrix, which has the information of the distance between students and schools among themselves; that is, a matrix of NxN must be proposed, where N is the total number of students plus the number of schools. The preparation of data is one of the sub-problems that have been least documented (J Park et al., 2010), especially the matrix of distances between nodes since this, usually, it is assumed or generated by some software and therefore not enough research has been devoted to this sub-problem.
Selection of bus stops: This sub-problem seeks to select a set of bus stops and assign students to these stops. However, some problems do not consider the possibility of bus stops but the students are picked up in their homes. this sub-problem can be divided into two classes: LAR, Location-Allocation-Routing and ARL, Allocation-Routing- Location, (J Park et al., 2010).
Generation of routes. This sub-problem is directly related to the problem of vehicle routing. Its objective is to determine the route of each bus, seeking to optimize the indicators according to the desired priority and the objectives of the distance matrix. The generation of routes is constituted in a VRP and its solution methods can be ex-act, heuristic, metaheuristics or specialized software.
Adjust to the school bell. Although in most school bus routing problems the start and end times of the routes are restrictions that are assumed to be constants of the problem, in some problems these can be decision variables to find the optimal time of initialization or completion to maximize the number of students that can be picked up by the same bus and in this way, reduce the number of used buses. This is one of the sub-problems that have been least treated in the literature (J Park et al., 2010), (Desrosiers et al., 1981). This variant implies the modification of the start of classes and no importance is given to the time students spend on the bus to give priority to the optimization of the productivity of the vehicle fleet.
Bus programming. This sub-problem occurs when there are routing situations of school buses with more than one school. The bus schedule defines the exact start and end time of the different bus routes. (Rita M. Newton & Thomas, 1974) develop a model that determines the programming of buses for different schools in the same district assuming that the time windows of the schools are different and allowing students from different schools to board the same bus. One of the strongest restrictions when dealing with SBRP with multiple schools is the time of entry to them, since all the works that have been done take into account more than one school assuming that their hours of entry are not equal.
The time dependent SBRP, tries to introduce the effect of aspects such as congestion and weather to the routing problem. In such a way that it states that the time between a node and another node does not remain constant over time, that is, said time can change depending on the moment in which the journey begins. Recently this problem has attracted great interest from different researchers and several important researches have been developed. Below, some are exposed and grouped according to the solution strategy used.
Exact methods. (Bhusiri, Qureshi, & Taniguchi, 2014) present a Branch and price for VRP with soft time windows with penalties, considering the time-dependent arrivals. On the other (Dabia, Ropke, van Woensel, & De Kok, 2013) present a Branch and price for TDVRPTW minimizing the time spent on the route. (Dohn, Rasmussen, & Larsen, 2011) solve the problem based on a column generation strategy. (Koc, Karaoglan, Koç, & Karaoʇlan, 2014) develop a linear programming model for the time dependent problem, where no subsequent output of a node can first arrive at a previous, First-In, First-Out. Another alternative modeling is presented in (H.-F. Wang & Lee, 2011). (Y. Y. . Kuo, Wang, & Chuang, 2009) work in the optimization of the allocation of the merchandise in the time dependent VRP. A time dependent VRP is developed in Mancini (Mancini, 2014) taking into account the vehicular congestion, having as a real case study in Torino. A model for the stochastic TDVRP is presented in (Nahum & Hadas, 2009) and a linear programming model for the two step TDVRP for cold chain logistics are presented in (Soysal, Bloemhof-Ruwaard, Bektas, et al., 2015), it takes into account the emissions and multiple variables of real life.
Heuristics. The time dependent VRP has been treated with different types of heuristics, for example developments based on constructive Heuristics can be seen in (Afshar-Nadjafi & Afshar-Nadjafi, 2014; Z Duan, Yang, Sun, & Wang, 2010). Developments that involve dynamic programming heuristics are found in (Kok, Hans, & Schutten, 2012; Kok, Hans, Schutten, & Zijm, 2010; Li, Li, & Gao, 2012); also other different heuristics are presented and compared in (Andres Figliozzi & Figliozzi, 2012; H.-K. Chen, Hsueh, & Chang, 2006; Hu & Tang, 2009; Huart, Perron, Caporossi, & Duhamel, 2016; Malandraki & Daskin, 1992). A hierarchy algorithm for the TDVRP in intelligent transport systems is presented in (Nejad, Mashayekhy, Chinnam, & Phillips, 2016).
Metaheuristics. The metaheuristics found in the references to address the time de-pendent VRP are presented below: The genetic algorithm application can be seen in (Haghani & Jung, 2005; Jung & Haghani, 2001; Liu, Lin, Chiu, Tsao, & Wang, 2014; Tang, Shi, & Meng, 2008; X. Wang, Yang, & Tian, 2013; Xin, Goncalves, & Dupas, 2008; X. Zhao, Goncalves, & Dupas, 2009). Different researches about the Ant Colony Strategy can also be found, for example (Balseiro, Loiseau, & Ramonet, 2011; B. Chen, Song, & Chen, 2007; Donati, Montemanni, Casagrande, Rizzoli, & Gambardella, 2008; Z.-Y. Duan, Yang, & Wang, 2010; Zhengyu Duan, Sun, Sun, & Li, 2015). Some ant colony hybrids with tabu search can be seen in (Zare-Reisabadi & Mirmohammadi, 2015). Applications with pure tabu search are found in (Ceschia, Di Gaspero, & Schaerf, 2011; Cordeau & Laporte, 2001; Jabali, Van Woensel, De Kok, Lecluyse, & Peremans, 2009; Nguyen, Crainic, & Toulouse, 2013; Setak et al., 2015; Taş et al., 2014; Z.-G. Wang, Liu, & Wang, 2006; Zare-Reisabadi & Mirmohammadi, 2015). Other heuristics have been applied less frequently in the literature, for example different local search algorithms can be seen in (Demirel, Demirel, & Tasdelen, 2008; Hashimoto, Yagiura, & Ibaraki, 2008; S.a Kritzinger, Tricoire, Doerner, & Hartl, 2011; Stefanie Kritzinger et al., 2012; Taş et al., 2014). On the side of the PSO, or particle cloud you have (Mousavipour & Hojjati, 2014; N Norouzi, Sadegh-Amalnick, & Tavakkoli-Moghaddam, 2016; Narges Norouzi, Sadegh-Amalnick, & Tavakkoli-Moghaddam, 2015; Y. Zhao, Wu, Wang, & Zhang, 2008). Some applications are also found using the heuristic goal of simulated annealing, see for example (Y. Kuo, 2010; Narges Norouzi et al., 2015).
In the review it is identified that the time dependent VRP has been treated with different approach, from optimization to heuristics, however, the specific problem in the routing of school buses has not been addressed until the present revision, although authors agree that it is important to involve the effects of traffic on the problem.
In this sense, a mathematical model is developed below for the problem of school bus routing with simple load, assuming buses start at school and end there. It is considered a heterogeneous fleet.
It is assumed that a node can only go one vehicle to avoid confusion in the boarding of children. They are considered windows of time for the entrance to the school. Time Dependent are considered depending on traffic, it is not allowed that the vehicle once starting stop to wait for the traffic to go down. It is assumed that the children are picked up door to door and it seeks to minimize the duration of the route with the longest travel time.
Based on the models presented in (X. Chen et al., 2015a; Ebensperger, 2009; Haghani & Jung, 2005), the following proposed model is presented in which the time dependent SBRP with the characteristics presented above are introduced.


The tvitj parameter is presented in table 2. The times of the school trip (node 0) are presented to all the other nodes for each of the time intervals, an equal table was developed for each node in relation to the others.
Table 2
Time Dependent for i=0
[0, t, j]: |
Nodes |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Periods |
1 |
0 |
5 |
4 |
1 |
3 |
1 |
2 |
2 |
0 |
6 |
5 |
2 |
4 |
2 |
3 |
|
3 |
0 |
7 |
6 |
3 |
5 |
3 |
4 |
|
4 |
0 |
9 |
8 |
5 |
7 |
5 |
6 |
Fig. 1 shows the behavior of the travel times for school to node one, in the different periods of time with the duration of their respective intervals.
Fig. 1
Time Dependent of the arc between the school and node one
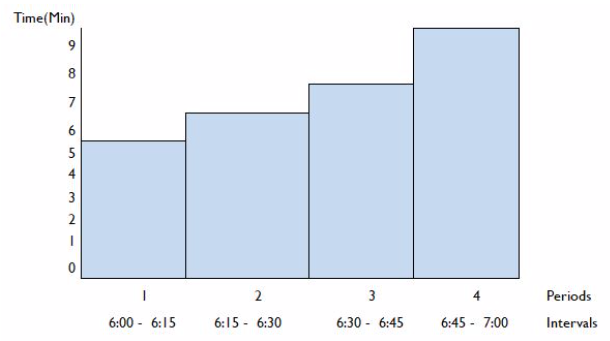
Table 3 and 4 respectively show the details of the vehicles and the nodes.
Table 3
Vehicle details
Vehicle |
Capacity ( #kids) |
1 |
4 |
2 |
4 |
3 |
3 |
-----
Table 4
Node details
Nodes |
at |
q (#Kids) |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
1 |
2 |
3 |
1 |
2 |
4 |
1 |
1 |
5 |
2 |
5 |
6 |
1 |
1 |
It is established that vehicles can not arrive at school before 6:45 am and cannot arrive later than 6:55 am, for this reason it is assumed that the time of service in the school is zero, since it is assumed that if a vehicle arrives at 6:55 am, which is the end of the school time window, in the remaining time until 7:00 a.m., which is the beginning of the day, the children reach to get out of the vehicle and reach the classroom.
The proposed model was implemented in AMPL® and the presented instance was resolved through the Neos Server, using the CPLEX AMPL solver. Next, in figure 2, the detail of the route 1 is presented. The ovals represent the visited nodes and the circles the time intervals.
Since the window of time, at school starts at interval three, that is, at 6:45 a.m., and keeping in mind that the vehicle does not wait at any other node, it is identified that the model ends the route 1 at the earliest time, and synchronizes the ones collected backwards according to that time. The foregoing indicates that arriving later represents incurring in longer travel times, since the final intervals are the ones that are most affected by traffic.
Route 2 goes from school to node 5 in interval 2, from node 5 to 4 in interval 3 and arrives at school in interval three at 6:45 a.m. Route 3 leaves the school at node 1 in interval 2, then goes to node 3 in interval 3 and finally to school in interval 3.
Given the characteristics of the objective function in terms of guaranteeing that the child who delays the most, does so in the shortest possible time, the model is forced to balance the routes, which is evident since the departure time of the three School routes is 6.29 a.m. and all arrive at 6:45 a.m. Which evidences the interest to arrive at the earliest time of the route for what was mentioned above, and the balance of the routes required in the performance function.
Fig. 2
Details of route 1

The revised bibliography allows to identify that the time dependent SBRP has not been addressed before, although there are developments in the routing, in general they have not been presented for this specific class of problems, which places this research within the framework of an extension of the field of knowledge for a specific class of problem.
The routing of school buses is a class of VRP, however it has particular elements that make that the considerations of some characteristics have a specific impact on the problem, as for example the case of performance functions, that can go beyond the economic, because people are transported and the social and environmental dimensions have an important role in the evaluation of a solution.
The consideration of not waiting at the nodes beyond the planned time of attention generates that the model runs the time of departure and incur longer travel times. The above follows the importance of addressing this same problem in a multi-objective environment, this in the sense that reducing fuel consumption, for example, can cause it to leave during low traffic hours, however, this would cause children to have to wait in a node or outside the school, which increases their time spent on the road or the time between leaving home and being in school.
Finally, it is important to test the scalability of the model since the problem grows exponentially depending on the nodes, heterogeneity of the vehicles or time periods, in that sense it is important to explore other strategies, such as heuristic goal or artificial intelligence as genetic programming.
Afshar-Nadjafi, B., & Afshar-Nadjafi, A. (2014). A constructive heuristic for time-dependent multi-depot vehicle routing problem with time-windows and heterogeneous fleet. Journal of King Saud University - Engineering Sciences. https://doi.org/http://dx.doi.org/10.1016/j.jksues.2014.04.007
Andres Figliozzi, M., & Figliozzi, M. (2012). The time dependent vehicle routing problem with time windows: Benchmark problems, an efficient solution algorithm, and solution characteristics. Transportation Research Part E: Logistics and Transportation Review, 48(3), 616–636. https://doi.org/10.1016/j.tre.2011.11.006
Balseiro, S., Loiseau, I., & Ramonet, J. (2011). An Ant Colony algorithm hybridized with insertion heuristics for the Time Dependent Vehicle Routing Problem with Time Windows. Computers and Operations Research, 38(6), 954–966. https://doi.org/10.1016/j.cor.2010.10.011
Bhusiri, N., Qureshi, A. G., & Taniguchi, E. (2014). The trade-off between fixed vehicle costs and time-dependent arrival penalties in a routing problem. Transportation Research Part E: Logistics and Transportation Review, 62, 1–22. https://doi.org/http://dx.doi.org/10.1016/j.tre.2013.12.003
Bögl, M. M. ., Doerner, K. F. K. F. . b c K. F., & Parragh, S. N. . d S. N. (2015). The School Bus Routing and Scheduling Problem with Transfers. Networks, 65(1), 180–203. https://doi.org/10.1002/net.21589
Braca, J., Bramel, J., Posner, B., & Simchi-Levi, D. (1997). A computerized appraoch to the New York City school bus routing problem. IIE Transactions, 28, 8, 693–702.
Ceschia, S., Di Gaspero, L., & Schaerf, A. (2011). Tabu search techniques for the heterogeneous vehicle routing problem with time windows and carrier-dependent costs. Journal of Scheduling, 14(6), 601–615. https://doi.org/10.1007/s10951-010-0213-x
Chen, B., Song, S., & Chen, X. (2007). A multi-ant colony system for vehicle routing problem with time-dependent travel times. In Proceedings of the IEEE International Conference on Automation and Logistics, ICAL 2007 (pp. 446–449). https://doi.org/10.1109/ICAL.2007.4338604
Chen, H.-K., Hsueh, C.-F., & Chang, M.-S. (2006). The real-time time-dependent vehicle routing problem. Transportation Research Part E: Logistics and Transportation Review, 42(5), 383–408. https://doi.org/10.1016/j.tre.2005.01.003
Chen, X., Kong, Y., Dang, L., Hou, Y., & Ye, X. (2015). Exact and metaheuristic approaches for a bi-objective school bus scheduling problem. PLoS ONE, 10(7), 1–20. https://doi.org/10.1371/journal.pone.0132600
Cordeau, J. F., & Laporte, G. (2001). A tabu search algorithm for the site dependent vehicle routing problem with time windows. INFOR, 39(3), 292–298.
Dabia, S., Ropke, S., van Woensel, T., & De Kok, T. (2013). Branch and Price for the Time-Dependent Vehicle Routing Problem with Time Windows. Transportation Science, 47(3), 380–396. https://doi.org/10.1287/trsc.1120.0445
Demirel, T., Demirel, N. C., & Tasdelen, B. (2008). Time dependent vehicle routing problem with fuzzy traveling times under different traffic conditions. Journal of Multiple-Valued Logic And Soft Computing, 14(3–5), 387–400.
Desrosiers, J., Ferland, J. A., Rousseau, J.-M., Lapalme, G., & Chapleau, L. (1981). An Overview of a School Busing System. In N. K. Jaiswal (Ed.), Scientific Management of Transport Systems (pp. 235–243). North-Holland.
Dohn, A., Rasmussen, M. S., & Larsen, J. (2011). The vehicle routing problem with time windows and temporal dependencies. Networks, 58(4), 273–289. https://doi.org/10.1002/net.20472
Donati, A., Montemanni, R., Casagrande, N., Rizzoli, A., & Gambardella, L. (2008). Time dependent vehicle routing problem with a multi ant colony system. European Journal of Operational Research, 185(3), 1174–1191. https://doi.org/10.1016/j.ejor.2006.06.047
Duan, Z.-Y., Yang, D.-Y., & Wang, S. (2010). Improved ant colony optimization algorithm for time-dependent vehicle routing problem. Kongzhi Lilun Yu Yingyong/Control Theory and Applications, 27(11), 1557–1563. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-78650933767%7B&%7DpartnerID=40%7B&%7Dmd5=3b03401996951b19a952f8ac9102dcad
Duan, Z., Sun, S., Sun, S., & Li, W. (2015). Stochastic time-dependent vehicle routing problem: Mathematical models and ant colony algorithm. Advances in Mechanical Engineering, 7(11), 1–16. https://doi.org/10.1177/1687814015618631
Duan, Z., Yang, D., Sun, W., & Wang, S. (2010). Route construction algorithms for time dependent vehicle routing problem. In ICLEM 2010: Logistics for Sustained Economic Development - Infrastructure, Information, Integration - Proceedings of the 2010 International Conference of Logistics Engineering and Management (Vol. 387, pp. 3467–3474). Chengdu. https://doi.org/10.1061/41139(387)484
Ebensperger, M. (2009). Una formulación para el problema de ruteo de vehículos con tiempos de viaje dependientes del timpo para la actualización de turas con información en tiempo real.
Ehmke, J. F., Campbell, A. M., & Thomas, B. (2016). Vehicle routing to minimize time-dependent emissions in urban areas. European Journal of Operational Research, 251(2), 478–494. https://doi.org/10.1016/j.ejor.2015.11.034
Ellegood, W. A., Campbell, J. F., & North, J. (2015). Continuous approximation models for mixed load school bus routing. Transportation Research Part B-Methodological, 77, 182–198. https://doi.org/10.1016/j.trb.2015.03.018
Fügenschuh, A., & Martin, A. (2006). A multicriteria approach for optimizing bus schedules and school starting times. Annals of Operations Research, 147(1), 199–216. https://doi.org/10.1007/s10479-006-0066-z
Haghani, A., & Jung, S. (2005). A dynamic vehicle routing problem with time-dependent travel times. Computers and Operations Research, 32(11), 2959–2986. https://doi.org/http://dx.doi.org/10.1016/j.cor.2004.04.013
Hashimoto, H., Yagiura, M., & Ibaraki, T. (2008). An iterated local search algorithm for the time-dependent vehicle routing problem with time windows. Discrete Optimization, 5(2), 434–456. https://doi.org/10.1016/j.disopt.2007.05.004
Hu, M.-W. ., & Tang, H. . (2009). Efficient heuristics for vehicle routing problems with time-dependent travel times. Shenzhen Daxue Xuebao (Ligong Ban)/Journal of Shenzhen University Science and Engineering, 26(3), 315–320. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-68749085957%7B&%7DpartnerID=40%7B&%7Dmd5=7744644a13e36351b265c0d50aa6451a
Huart, V. ., Perron, S. ., Caporossi, G. ., & Duhamel, C. . (2016). A heuristic for the time-dependent vehicle routing problem with time windows. Lecture Notes in Economics and Mathematical Systems, 682, 73–78. https://doi.org/10.1007/978-3-319-20430-7_10
Jabali, O., Van Woensel, T., De Kok, A. G., Lecluyse, C., & Peremans, H. (2009). Time-dependent vehicle routing subject to time delay perturbations. IIE TRANSACTIONS, 41(12), 1049–1066. https://doi.org/10.1080/07408170902976194
Jung, S., & Haghani, A. (2001). Genetic algorithm for the time-dependent vehicle routing problem. Proceedings of the 5th World Congress on Intelligent Transport Systems, (1771), 164–171.
Kang, M., Kim, S.-K. S., Felan, J. T., Choi, H. R., & Cho, M. (2015). Development of a Genetic Algorithm for the School Bus Routing Problem. International Journal of Software Engineering and Its Applications, 9(5), 107–126. https://doi.org/10.14257/ijseia.2015.9.5.11
Kinable, J., Spieksma, F. C. R., & Vanden Berghe, G. (2014). School bus routing-a column generation approach. International Transactions in Operational Research, 21(3), 453–478. https://doi.org/10.1111/itor.12080
Koc, C., Karaoglan, I., Koç, Ç., & Karaoʇlan, I. (2014). Mathematical Model for The Time-Dependent Vehicle Routing Problem. Journal of the Faculty of Engineering and Architecture af Gazi University, 29(3), 549–558. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-84907552552%7B&%7DpartnerID=40%7B&%7Dmd5=a6078bcf3504da981984f6596a6ef6ef
Kok, A. L., Hans, E. W., & Schutten, J. M. J. (2012). Vehicle routing under time-dependent travel times: The impact of congestion avoidance. Computers and Operations Research, 39(5), 910–918. https://doi.org/10.1016/j.cor.2011.05.027
Kok, A. L., Hans, E. W., Schutten, J. M. J., & Zijm, W. H. M. (2010). A dynamic programming heuristic for vehicle routing with time-dependent travel times and required breaks. Flexible Services And Manufacturing Journal, 22(1–2, SI), 83–108. https://doi.org/10.1007/s10696-011-9077-4
Kritzinger, S. ., Tricoire, F. ., Doerner, K. F. . F. b, & Hartl, R. F. . F. (2011). Variable neighborhood search for the time-dependent vehicle routing problem with soft time windows. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 6683 LNCS, 61–75. https://doi.org/10.1007/978-3-642-25566-3_5
Kritzinger, S., Doerner, K., Hartl, R., Kiechle, G., Stadler, H., & Manohar, S. (2012). Using Traffic Information for Time-Dependent Vehicle Routing. Procedia - Social and Behavioral Sciences, 39, 217–229. https://doi.org/http://dx.doi.org/10.1016/j.sbspro.2012.03.103
Kuo, Y. (2010). Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Computers & Industrial Engineering, 59(1), 157–165. https://doi.org/http://dx.doi.org/10.1016/j.cie.2010.03.012
Kuo, Y. Y. ., Wang, C.-C., & Chuang, P.-Y. (2009). Optimizing goods assignment and the vehicle routing problem with time-dependent travel speeds. Computers and Industrial Engineering, 57(4), 1385–1392. https://doi.org/10.1016/j.cie.2009.07.006
Levin, M. W., & Boyles, S. D. (2016). Practice summary: Improving bus routing for KIPP charter schools. Interfaces, 46(2), 196–199. https://doi.org/10.1287/inte.2015.0817
Li, Y.-F. ., Li, J. ., & Gao, Z.-Y. . (2012). Dynamic programming heuristics for solving time dependent vehicle routing problem. Xitong Gongcheng Lilun Yu Shijian/System Engineering Theory and Practice, 32(8), 1712–1718. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-84867411815%7B&%7DpartnerID=40%7B&%7Dmd5=8ba904075f28f80ea9e5180a669b7da7
Liu, W.-Y. W.-Y., Lin, C.-C. C.-C., Chiu, C.-R. C.-R., Tsao, Y.-S. Y.-S., & Wang, Q. (2014). Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths. Sustainability (Switzerland), 6(7), 4658–4684. https://doi.org/10.3390/su6074658
Malandraki, C., & Daskin, M. S. (1992). Time Dependent Vehicle Routing Problems: Formulations, Properties and Heuristic Algorithms. Transportation Science, 26(3), 185–200. https://doi.org/10.1287/trsc.26.3.185
Mancini, S. (2014). Time dependent travel speed vehicle routing and scheduling on a real road network: The case of torino. In Transportation Research Procedia (Vol. 3, pp. 433–441). Elsevier. https://doi.org/10.1016/j.trpro.2014.10.024
Mousavipour, S., & Hojjati, S. M. H. (2014). A particle swarm optimisation for time-dependent vehicle routing problem with an efficient travel time function. International Journal of Operational Research, 20(1), 109–120. https://doi.org/10.1504/IJOR.2014.060518
Nahum, O. E., & Hadas, Y. (2009). Developing a model for the stochastic time-dependent vehicle-routingproblem. In 2009 International Conference on Computers and Industrial Engineering, CIE 2009 (pp. 118–123). Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-77956097656%7B&%7DpartnerID=40%7B&%7Dmd5=5005671c00b0bb0750218f797101d72c
Nejad, M. M., Mashayekhy, L., Chinnam, R. B., & Phillips, A. (2016). Hierarchical time-dependent shortest path algorithms for vehicle routing under ITS. IIE Transactions (Institute of Industrial Engineers), 48(2, SI), 158–169. https://doi.org/10.1080/0740817X.2015.1078523
Newton, R. M., & Thomas, W. H. (1969). Design of school bus routes by computer. Socio Economic Planning Sciences, 75–85.
Newton, R. M., & Thomas, W. H. (1974). Bus routing in a multi-school system. Computers & Operations Research, 1(2), 213–222. https://doi.org/https://doi.org/10.1016/0305-0548(74)90047-1
Nguyen, P. K., Crainic, T. G., & Toulouse, M. (2013). A tabu search for time-dependent multi-zone multi-trip vehicle routing problem with time windows. European Journal of Operational Research, 231(1), 43–56. https://doi.org/10.1016/j.ejor.2013.05.026
Norouzi, N., Sadegh-Amalnick, M., & Tavakkoli-Moghaddam, R. (2015). A Time-Dependent Vehicle Routing Problem Solved By Improved Simulated Annealing. Proceedings of the Romanian Academy Series A-Mathematics Physics Technical Sciences Information Science, 16(3), 458–465.
Norouzi, N., Sadegh-Amalnick, M., & Tavakkoli-Moghaddam, R. (2016). Modified particle swarm optimization in a time-dependent vehicle routing problem: minimizing fuel consumption. Optimization Letters, 1–14. https://doi.org/10.1007/s11590-015-0996-y
Park, J., & Kim, B.-I. (2010). The school bus routing problem: A review. European Journal of Operational Research, 202(2), 311–319. https://doi.org/10.1016/j.ejor.2009.05.017
Park, J., Tae, H., & Kim, B.-I. (2012a). A post-improvement procedure for the mixed load school bus routing problem. European Journal of Operational Research, 217(1), 204–213. https://doi.org/10.1016/j.ejor.2011.08.022
Park, J., Tae, H., & Kim, B. (2010). A Mixed Load Algorithm for the School Bus Routing Problem.
Rocha, L., González, E., & Orjuela, J. (2011). Una Revisión al Estado del Arte del Problema de Ruteo de Vehículos: Evolución Histórica Y Métodos De Solución. Ingeniería, 16(2), 35–55. Retrieved from http://revistas.udistrital.edu.co/ojs/index.php/reving/article/view/3832
Sankaran, J., & Wood, L. (2007). The relative impact of consignee behaviour and road traffic congestion on distribution costs. Transportation Research Part B: Methodological, 41(9), 1033–1049. https://doi.org/10.1016/j.trb.2007.04.005
Schittekat, P., Kinable, J., Sörensen, K., Sevaux, M., Spieksma, F., & Springael, J. (2013). A metaheuristic for the school bus routing problem with bus stop selection. European Journal of Operational Research, 229(2), 518–528. https://doi.org/10.1016/j.ejor.2013.02.025
Setak, M., Habibi, M., Karimi, H., & Abedzadeh, M. (2015). A time-dependent vehicle routing problem in multigraph with FIFO property. Journal of Manufacturing Systems, 35, 37–45. https://doi.org/10.1016/j.jmsy.2014.11.016
Silva, C. M., Sarubbi, J. F. M., Silva, D. F., Porto, M. F., & Nunes, N. T. R. (2015). A Mixed Load Solution for the Rural School Bus Routing Problem. In IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC (Vol. 2015–Octob, pp. 1940–1945). Institute of Electrical and Electronics Engineers Inc. https://doi.org/10.1109/ITSC.2015.314
Souza Lima, F. M. . F. M. F. M. ., Pereira, D. S. D. S. . D. S., Conceição, S. V. . S. V., Ramos Nunes, N. T. N. T. ., de Souza Lima, F. M., Doro Pereira, D. S., Ramos Nunes, N. T. N. T. . (2016). A mixed load capacitated rural school bus routing problem with heterogeneous fleet: Algorithms for the Brazilian context. Expert Systems with Applications, 56, 320–334. https://doi.org/10.1016/j.eswa.2016.03.005
Soysal, M., Bloemhof-Ruwaard, J. M., Bektas, T., Bektaş, T., Bektas, T., & Bektaş, T. (2015). The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations. International Journal of Production Economics, 164(August 2013), 366–378. https://doi.org/10.1016/j.ijpe.2014.11.016
Spada, M., Bierlaire, M., & Liebling, T. M. (2005). Decision-aiding methodology for the school bus routing and scheduling problem. Transportation Science, 39(4), 477–490. https://doi.org/10.1287/trsc.1040.0096
Tang, J., Shi, W., & Meng, L. (2008). Time-dependent dynamic vehicle routing based on genetic algorithm. Wuhan Daxue Xuebao (Xinxi Kexue Ban)/ Geomatics and Information Science of Wuhan University, 33(8), 875–879. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-54549088789%7B&%7DpartnerID=40%7B&%7Dmd5=1e659839e42501aacf92ebcff9bd5170
Taş, D., Dellaert, N., van Woensel, T., de Kok, T., Tas, D., Dellaert, N., … de Kok, T. (2014). The time-dependent vehicle routing problem with soft time windows and stochastic travel times. Transportation Research Part C, 48, 66–83. https://doi.org/10.1016/j.trc.2014.08.007
Wang, H.-F., & Lee, Y.-Y. (2011). Modeling of a Time Dependent Alternative Vehicle Routing Problem with Time Windows. In International Conference on Management and Service Science, MASS 2011. Wuhan. https://doi.org/10.1109/ICMSS.2011.05998240
Wang, X., Yang, J., & Tian, Y. (2013). Enterprise transfer alliance vehicle routing problem based on time-dependent fuzzy traveling time and its genetic algorithm. Liaoning Gongcheng Jishu Daxue Xuebao (Ziran Kexue Ban)/Journal of Liaoning Technical University (Natural Science Edition), 32(11), 1580–1584. https://doi.org/10.3969/j.issn.1008-0562.2013.11.031
Wang, Z.-G., Liu, Z.-Y., & Wang, H.-W. (2006). Reactive tabu search algorithm for time-dependent vehicle routing problem with backhauls. Jisuanji Jicheng Zhizao Xitong/Computer Integrated Manufacturing Systems, CIMS, 12(9), 1453–1458. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-33845201555%7B&%7DpartnerID=40%7B&%7Dmd5=4157ceab136c846f43352c7e76c2b4dc
Wen, L., & Eglese, R. (2015). Minimum cost VRP with time-dependent speed data and congestion charge. Computers & Operations Research, 56, 41–50. https://doi.org/10.1016/j.cor.2014.10.007
Xin, Z., Goncalves, G., & Dupas, R. (2008). A genetic approach to solving the vehicle routing problem with time-dependent travel times. In 2008 Mediterranean Conference on Control and Automation - Conference Proceedings, MED’08 (pp. 413–418). https://doi.org/10.1109/MED.2008.4602216
Zare-Reisabadi, E., & Mirmohammadi, S. H. (2015). Site dependent vehicle routing problem with soft time window: Modeling and solution approach. COMPUTERS {&} INDUSTRIAL ENGINEERING, 90, 177–185. https://doi.org/10.1016/j.cie.2015.09.002
Zhao, X., Goncalves, G., & Dupas, R. (2009). On-line genetic algorithm for the dynamic vehicle routing problem withreal-time time-dependent travel times. In 2009 International Conference on Computers and Industrial Engineering, CIE 2009 (pp. 1052–1057).
Zhao, Y., Wu, B., Wang, W., & Zhang, J. (2008). Particle swarm optimization for Open Vehicle Routing Problem with Time Dependent Travel Time. In IFAC Proceedings Volumes (IFAC-PapersOnline) (Vol. 17). https://doi.org/10.3182/20080706-5-KR-1001.2843
Ziliaskopoulos, A., & Waller, S. (2000). An Internet-based geographic information system that integrates data, models and users for transportation applications. Transportation Research Part C: Emerging Technologies, 8(1–6), 427–444. https://doi.org/10.1016/S0968-090X(00)00027-9
1. Escuela de ingeniería industrial. Universidad del Valle. juan.orejuela@correounivalle.edu.co. Universidad Nacional de Colombia, estudiante del Doctorado en Ingeniería: Industria y Organizaciones sede Bogotá jporejuelac@unal.edu.co.
2. Departamento Ingeniería de Sistemas e Industrial. Universidad Nacional de Colombia. gjhernandezp@unal.edu.co