

 Vol. 39 (Nº 46) Año 2018. Pág. 3
Vol. 39 (Nº 46) Año 2018. Pág. 3
Dorys Jeannette MORALES Jaime 1
Recibido: 20/06/2018 • Aprobado: 05/07/2018
RESUMEN: Este artículo presenta los resultados del trabajo de grado a nivel doctoral titulado “Estrategias Metacognitivas de los Docentes de primaria, en Resolución de Problemas de Fracción Parte-Todo”. Que indaga sobre las estrategias metacognitivas que se activan en la resolución de problemas, durante el proceso de comprensión de la situación problema con el concepto de fracción parte todo, en contextos continuo, discreto, como razón, las habilidades pedagógicas y epistemológicas de docentes en ejercicio que orientan matemáticas en básica primaria en Boyacá, Colombia. |
ABSTRACT: This article presents the results of the doctoral level work entitled "Metacognitive Strategies of Primary Teachers, in Fraction Problem Resolution Part-All". That investigates metacognitive strategies that are activated in the resolution of problems, during the process of understanding the understanding the problem situation with the concept of fraction part all, in continuous, discrete contexts, as reason the pedagogical and epistemological skills of practices in the exercise that guide the math in basic primary in Boyacá, Colombia. |
Actualmente la educación a nivel del país, en las pruebas nacionales presentan bajo desempeño en los estudiantes, en la competencia de resolucionar problemas, no sólo a nivel primaria, sino secundaria, respecto al aprendizaje con en el tema de la fracción como parte-todo, en contextos discretos, continuos y como razón correspondiente al componente numérico - variacional.
Estas debilidades se evidencian en los bajos resultados que presentan los estudiantes en las pruebas nacionales e internacionales, a través de las respuestas dadas a los problemas con el concepto de fracción, involucra a los docentes en esa problemática. Diversas investigaciones a nivel nacional e internacional, (Ordoñez, (2012); Pontón, (2008); Gaviria, (2016); Castro, (2015) en sus conclusiones, llegan al mismo desenlace.
Se trabajaron teóricos como Pintrich et al, (1991, 1993); Flavell, (1979); Weinstein y Mayer, (1982); Llinares, (1997, 2004); Ball et al, (2001, 2008); Polya, (1954) y Poggioli, (1983, 2001), Shulman, (1986), en las diferentes temáticas que aborda la investigación: estrategias metacognitivas, resolución de problemas, la fracción parte- todo en contextos continuo, discreto, como razón y las competencias del docente que enseña matemáticas entre otros. De igual forma, Lago, Gamboa y Montes (2013), quienes consideran la resolución de problemas como herramienta metacognitiva que permite el aprendizaje de contenidos matemáticos, a través de la reflexión de los alumnos y docentes en los procesos de resolución, lo cual privilegia la socialización, la formación de la consciencia moral y los procesos educativos asociados al desarrollo de la autonomía, lo que implica una identidad propia como sujeto de derecho donde el niño tenga su espacio que le permita crecer, jugar y desarrollarse.
De ahí, la importancia que adquiere esta investigación, por cuanto se indagó a través de la identificación de las estrategias metacognitivas de planeación, control y regulación, los procesos y habilidades de los docentes, en la etapa de comprensión del problema, cuando resolucionan problemas con el concepto y uso de la fracción como parte-todo, en 67 Instituciones públicas del departamento de Boyacá, Colombia.
Los aspectos metodológicos tuvieron las siguientes fases de acuerdo al tipo de investigación cualitativa: En la fase preparatoria se hizo el diseño de instrumentos y reflexión sobre los aspectos a tratar en la investigación. En la fase de trabajo de campo, se aplicaron los instrumentos para recoger la información, tales como pruebas de presaberes, talleres de situaciones problemas, entrevistas semi-estructuradas, diarios de campo y se hizo la reflexión sobre el proceso. En la fase analítica se procedió a analizar el contenido de las pruebas de presaberes, los talleres, entrevistas y diarios de campo, con el fin de interpretar las respuestas de los docentes y sus habilidades, realizando la triangulación de los datos haciendo un análisis textual y la reflexión final. En la fase informativa, se consolidó el informe final del estudio y se generaron conclusiones y recomendaciones.
La metacognición la conciben los docentes, como un proceso asociado a un conocimiento o aprendizaje acompañado de una capacidad mental que poseen las personas sobre una situación que realizan. En detalle, para los docentes urbanos, la metacognición es como un proceso personal que relaciona experiencias y capacidades existentes con un nuevo aprendizaje, mientras que para los docentes rurales es un proceso de reflexión, donde un individuo es consciente de los conocimientos, procedimientos y competencias que tiene frente al desarrollo de una situación.
Sin embargo al comparar las concepciones epistemológicas de los docentes con sus prácticas propias se evidencio que el 79% de los docentes (53) presentan procesos mecánicos que conllevan a una habilidad de uso de algoritmos matemáticos, donde presentan un afán de dar respuesta numérica, de forma rápida, pero no hay un proceso de reflexión para organizar y comprender el planteamiento de la situación problema, dejando entrever que no se ha desarrollado en el docente mismo la consolidación de las estrategias metacognitivas, quizás porque consideran que la matemática es tan solo hacer uso de procesos algorítmicos que conllevan a una respuesta numérica (ejercitación), dejando de lado la importancia que se tiene en el macro proceso de la resolución de problemas y específicamente en el proceso de comprensión de la situación problema, que hace parte de la etapa de identificación del problema.
Es de notar que las habilidades pedagógicas empleadas por los docentes presentaron un porcentaje del 21% (1 urbano y 13 rurales), al resolucionar situaciones problemas con el uso del concepto de fracción parte – todo no realizan ningún proceso o esquema; es decir, ellos no permiten evidenciar ningún tipo de actividad frente al proceso de resolución de la situación problema, porque dejaron en blanco la hoja y algunos con un esquema incipiente que no permitió evidenciar información alguna; esto indica que hay un alto porcentaje de dificultad en los docentes para representar sus estrategias metacognitivas y consolidar los procesos de planeación, control y regulación, como también ausencia en las estrategias de repaso, organización y pensamiento crítico enunciadas por Pintrich y García (1993).
Al analizar las respuestas características y la práctica de los docentes participantes de la investigación a la luz del teórico Flavell (1979), se observó que para ellos no hay una comprensión y proceso consciente “es la relación de su propio conocimiento a partir del cual la propia persona toma conciencia de sus procesos y situaciones de aprendizaje”, lo cual implica que los docentes al resolucionar problemas matemáticos deben realizar inspección permanente, la ordenación de los pasos ejecutados para alcanzar una eficiencia de la tarea a desarrollar en la situación problema, habilidades fundamentales que se deben tener en cuenta en el proceso de enseñanza - aprendizaje en el área de matemática, lo que permitió inferir que no es importante para ellos generar una autorregulación de sus propios conocimientos, en pro de crear estrategias eficaces para desarrollar una tarea.
Al comparar las respuestas características (análisis textual) con la observación directa (diario de campo) en el desarrollo de los talleres, se evidenció que los docentes urbanos y rurales no presentan estructuras claras frente a la etapa de comprensión del problema dado que no logran identificar el contexto de la situación problema, diferenciar entre restricciones y datos, específicamente no se logra identificar la tarea, para ellos la comprensión del problema está ligado al uso de los procesos algorítmicos, antes de consolidar estrategias metacognitivas que permitieran identificar la comprensión de la situación problema; se podría decir que el bajo desempeño que tienen los docentes cuando enfrentan la resolución de problemas matemáticos se equipara con los bajos resultados de los estudiantes en esta competencia y su bajo desempeño en las pruebas nacionales, a pesar de estar realizando, en forma constante, en la vida escolar este tipo de problemas; lo anterior permitió concluir que los docentes no presentan habilidades propias de la resolución de problemas matemáticos y existe vacíos en los actividades para la etapa de comprensión del problema. En los docentes se muestra ausencia en los pasos o elementos que se deben tener en cuenta en la comprensión de la situación problema; sin embargo, los rurales presentan una mayor aproximación que los urbanos que participaron en la investigación.
Sintetizando este apartado, al realizar un análisis desde las preguntas orientadoras, las cuales estaban destinadas a identificar como los docentes abordan y consolidan la etapa de comprensión de la situación problema en matemáticas, que permitieran conocer los conceptos de algunos elementos básicos para esta etapa, como identificación del contexto, restricciones, datos, información, tarea, se logró evidenciar por sus respuestas características (análisis textual) y con la observación directa (diario de campo) que cuando desarrollan el taller, tanto los docentes urbanos como los rurales, no tuvieron una cultura de análisis y consolidación de esta etapa, parece que hay gran dificultad al diferenciar estos conceptos, ellos no logran ser eficientes en la identificación del contexto de la situación problema, hubo una nula identificación del contexto como una confusión entre las restricciones, datos, información y tarea en las respuestas; por lo tanto se puede concluir que lo docentes presentan dificultad en la etapa de comprensión de la situación problema y por ende no tienen habilidad en la resolución de problemas y que sus estrategias metacognitivas de planeación, control y regulación fueron muy incipientes, casi ausentes.
Al hacer un análisis de los enunciados de la etapa de comprensión del problema a partir de situaciones particulares a la situación problema, pero que implícitamente conllevan al uso de las mismas estrategias, para de esta manera comparar los niveles de comprensión y uso del concepto de fracción parte-todo como razón, así como la identificación de los elementos importantes y jerárquicos, para generar estrategias metacognitivas en la etapa de comprensión de la situación problema, se evidenció que tanto los docentes urbanos como los rurales, presentaron dificultad en conceptos usados en el aula, no hay una identificación clara entre incógnitas, datos y condiciones, como también dificultad en la representaciones de la situación problema.
Se logró llegar a este conocimiento de procesos matemáticos, aplicando tanto la teoría de Mayer (1987) sobre procesos y conocimientos específicos, donde se presenta el modelo de resolución de problemas matemáticos, fundamentado en procesos de comprensión y solución, como también la tipificación de las estrategias a partir de diferentes tipos de representación considerados por Morales (2008), esquemas de los conocimientos lingüístico, semántico y esquemático, correspondientes al proceso de comprensión del problema correlacionado a las estrategias metacognitivas evidenciadas en los procedimientos ejecutados por los docentes cuando resolucionan las situaciones problemas planteadas a lo largo de toda la fase de campo de la investigación
Es así, como se logró identificar que 21 docentes que corresponden al 33% de los docentes que presentaron procesos en la resolución de problemas, tienen conocimiento lingüístico (11 rurales y 10 urbanos) dado que presentan una gran habilidad en el planteamiento del problema en un lenguaje simbólico, abordando de forma directa un modelo algorítmico para la resolución de la situación problema; 8 docentes que corresponde al 10% evidencian un tipo de conocimiento semántico (4 rurales y 4 urbanos) representando los datos iniciales de la situación problema en un lenguaje natural, posteriormente transcriben del lenguaje natural a representaciones simbólicas y por ultimo abordan un modelo algorítmico; y 12 docentes que corresponden al 18% de los participantes presentan un tipo de conocimiento esquemático (11 rurales y 1 urbano) por cuanto, primero realizan un esquema gráfico de la información dada sobre la situación problema, luego codifican los datos a representaciones simbólicas y simultáneamente identifican un modelo matemático para la resolución de la situación problema.
Finalmente, un alto porcentaje de docentes, (26), el 39%, discriminados en (24 rurales y 2 urbanos), no realizan ningún proceso o esquema frente a la resolución de la situación problema dejando en blanco la hoja y algunos marcando alguna propuesta.
Lo anterior permite inferir, que los docentes no son conscientes sobre el tipo de conocimiento matemático que poseen, teniendo en cuenta lo que dice Mayer (1987), situación que requiere ser analizada a profundidad, para lograr mejores procesos educativos.
En la entrevista, los docentes asocian la resolución de problemas en un alto porcentaje del 78% con conceptos matemáticos y procesos algorítmicos, continuaron en un 69% con problemas ejecutados anteriormente en su práctica, el 35% dijo que en actividades realizadas por sus estudiantes y el 28% como tareas
Lo anterior permitió inferir que los docentes asocian la resolución de problemas con el currículo, como práctica, como elementos de la vida académica y escolar, no son concebidos como una competencia para la resolución de situaciones cotidianas y de la vida; además, la tarea no tiene mayor relevancia para ellos.
Esto permitió comprender la baja eficacia de resolución de problemas en situaciones cotidianas presentadas por los estudiantes en las pruebas nacionales e internacionales, ya que no se considera la resolución de problemas como una competencia matemática que contemple los procesos metacognitivos y cognitivos, como también su eficacia. De acuerdo a los autores Stanic y Kilpatrick (1998, p.3) quienes hacen un esquema sobre tres significados de la resolución de problemas en el área de matemáticas: “hacer matemáticas” el rol que los problemas juegan en la vida académica y ésta consiste que el trabajo de la matemática realmente consciente en problemas y soluciones, “como contexto” funcional en el currículo enmarca sus procesos desde los cinco roles: justificar la enseñanza matemática, como motivador para ciertos temas, como recreación, como medio para desarrollar nuevas habilidades, como práctica, “como habilidad” que corresponde a las concepciones pedagógicas y epistemológicas se direccionan a las técnicas de resolución de problemas enseñadas como un contenido, con problemas de práctica relacionados para que las técnicas puedan ser dominadas.
Al interpretar las respuestas características dadas por los docentes urbanos a las estrategias utilizadas para resolver una situación problema en matemáticas, sus estrategias apuntan a la codificación, aclaración y entendimiento de la información del problema, centrándose en la lectura, toma de datos para realizar y ejecutar un plan, mientras que en el grupo rural se observó una estructura más reflexiva, ya que además de realizar la lectura, toma de datos y elaboración de un esquema, hacen un análisis de las posibles restricciones, como una realimentación de los procesos generando un monitoreo de la acción del proceso.
Al comparar la concepción de los docentes sobre las estrategias para resolucionar problemas con el desarrollo empleado por ellos al abordar situaciones problemas matemáticos desde la observación directa (diario de campo) no hay una coherencia estructurada dado que tan solo permitió percibir algunos elementos de la comprensión del problema mostrando la poco eficiencia de los procesos empleados, lo que permitió deducir que los docentes deben consolidar desde su práctica las estrategias de resolución de problemas matemáticos correspondientes a las etapas de comprensión del problema, concepción de un plan, ejecución del plan y evaluación de la solución, que van más allá de solo la toma de datos, uso de la información y procesos algorítmicos, sin un proceso de planeación, regulación y control que permitiera mostrar una eficacia en la solución.
El empleo de estas estrategias mostraron poca eficacia en los docentes participantes, si se asocia con lo reflejado en los bajos resultados de los estudiantes del país en las pruebas externas, frente a la competencia de resolución de problemas, lo que permite reflexionar ¿cómo es que el docente concibe la resolución de problemas matemáticos? si es desde una acción algorítmica de ejercitación meramente numérica o como una creación de estructura mental consolidada en dos procesos: la comprensión del problema y de solución expuesta por Mayer (1982).
Aunque los dos grupos establecieron unos pasos donde priorizaron la lectura, la toma de datos, operaciones, representaciones y respuestas; las estrategias empleadas por ellos que podían ser validas desde su experiencia docente, el análisis vale la pena hacerlo a la luz de Poggioli (2001) quien establece estrategias generales en la resolución de problemas al margen del contenido o dominio específico de un problema, habilidades que debe tener el docente que enseña matemáticas al abordar una resolución de problemas como son: identificar el problema, abstraer información del problema, identificar la pregunta, definir las variables, formalizar la situaciones (ecuaciones), plantear alternativas de solución, aplicar una de las alternativa y evaluar la solución estrategias éstas que no se evidencian de forma clara y estructurada en los pasos ejecutados por ellos, ni en las cuatro fases de resolución de problemas establecidos por Polya (1954).
Por tal razón, los docentes que enseñan y orientan matemáticas en la educación básica primaria, deben conocer primero el método Polya para resolucionar problemas matemáticos y en segunda instancia, apropiarse del cómo se logra consolidar cada etapa para desarrollar estrategias claras en los estudiantes y por ende en ellos, para tener una eficacia en la competencia de la resolución de problemas.
Al comparar estas respuestas características con la observación directa (diario de campo) de los docentes cuando resolucionan situaciones problemas en los talleres hay una tendencia a procesar datos numéricos o mirarlo como una situación que requiere un solución única, pareciera que en el lenguaje de los docentes el resolucionar un problema matemático está ligado a una ejercitación y uso de algoritmos matemáticos que conllevan a un proceso de solución netamente numérico, sin detenerse en el proceso de comprensión, dado que no hay estrategias claras de planeación, regulación y control, sin embargo realizan procesos débiles de monitoreo y reflexión sobre las actividades realizadas, como la identificación de patrones para decidir con rapidez si la situación es un problema o un ejercicio, la aplicación de diversas tácticas y heurísticas, el análisis de los datos creando gráficos o esquemas que permitan comprender el problema, el recordar conocimientos involucrados, el determinar la exactitud y pertinencia de los datos disponibles para abordar la solución, siendo estos algunos elementos para la resolución de problemas considerados por Woods (2002), lo cual permite comprender su baja eficacia en sus soluciones.
Al retomar a Dijkstra (1991), citado por Bañuelos (1995, p.4), el autor considera que la “resolución de problemas es un proceso cognoscitivo complejo que involucra el conocimiento almacenado en la memoria de corto y largo plazo” cuando los docentes resolucionan problemas no es fácil evidenciar los conocimientos almacenados a largo plazo, quizás porque muy pocos docentes realizan un esquema de los pasos o estrategias a ejecutar, no consideran necesario realizar un esquema de las actividades y/u operaciones mentales que permita codificar, aclarar y entender la información de la situación problema; esto se evidencia en la observación directa (diario de campo) cuando los docentes resolucionan situaciones problemas en los talleres y muchos de ellos se limitan a encerrar la respuesta pero no hay procesos ni procedimiento alguno, dejando la hoja en blanco como se evidenció en el taller de pre-saberes donde el 39% de los docentes no presentaron esquema alguno en la solución, lo que no permite evidenciar procesos de planeación, control y regulación.
Lo anterior, permite inferir que los docentes, aunque manifiestan conocer y hacer uso de los referentes de calidad, en su práctica presentan un desconocimiento de los lineamientos matemáticos (Men, 1998) y comprensión de los estándares básicos de competencias matemáticas (Men, 2006) dado que no tienen claro lo que implica la competencia de la resolución de problemas desde este macro proceso en la enseñanza de las matemáticas.
Respecto del conocimiento y dominio que tienen los docentes del uso del concepto de fracción parte – todo, al analizar su eficacia a través de todo el proceso investigativo, se puede decir que los docentes tienen confusión conceptual en el uso de la fracción parte todo en contexto discreto y continuo, lo ejecutan de forma mecánica, no hay una conciencia clara de la diferencia entre ellos; en el uso de la razón, hay mayor dificultad, porque no hay una comprensión en el orden de relacionar las variables, presentando una baja eficiencia en la resolución de situaciones problemas escolares.
En síntesis, se puede afirmar que, el hecho de que el docente enseñe el concepto de fracción como parte de un todo en el aula, no implica la habilidad y el uso asertivo del mismo para el proceso en el aula, respecto de la resolución de problemas; de igual manera, vale la pena anotar que, existen diferentes tipos de conocimientos específicos que conllevan a estrategias propias del proceso, lo cual no garantiza la eficacia del proceso, pero si contribuye a la comprensión de la situación problema.
La entrevista que se realizó fue semi-estructurada y aplicada a todos los docentes urbanos y rurales que hacían parte del estudio; tenía como objetivo conocer las concepciones epistemológicas y pedagógicas que poseían los sesenta y siete docentes en ejercicio que orientaban matemáticas en básica primaria, en los establecimientos educativos públicos de las trece provincias del departamento de Boyacá, en el año 2017.
Se abordan algunas concepciones epistemológicas y pedagógicas desde la práctica de los docentes, específicamente sobre metacognición, estrategias metacognitivas, estrategias de resolución de problemas, habilidades matemáticas empleadas por ellos para resolucionar problemas matemáticos, de igual manera los procesos correspondientes a la etapa de comprensión del problema para identificar la tarea.
Dado que la investigación fue de corte cualitativo y específicamente con análisis textual, el software empleado fue el SPADT (SISTEM de análisis de datos textuales), el cual permite retomar algunos procesos ejecutados para este trabajo, a partir de cuatro momentos: el primero en la creación de un diccionario de palabras empleadas por los docentes en las respuestas cualitativas obtenidas en entrevista y talleres que organiza alfabéticamente; el segundo, la toma de las palabras características con mayor frecuencia empleada por todos los docentes participantes; el tercero, la realización de una lista de palabras características con valores de test y de probabilidad con criterio de chi-cuadrado de cada grupo (urbano y rural) , en el cuarto, se retomaron las respuestas características y significativas asociadas a la distribución de las distancias más cercanas al valor promedio de los participantes, por cada grupo urbano y rural, lo cual da validez científica a lo realizado.
A partir de esta información arrojada por el análisis textual se procedió a organizar y analizar las respuestas para garantizar la eficacia del proceso de la investigación a la luz del diario de campo y los referentes teóricos para triangular.
A continuación se presentan algunos resultados (análisis textual) que contienen las respuestas dadas por los docentes respecto de algunas de las preguntas más importantes formuladas en la entrevista:
Pregunta Uno: ¿Qué entiende Usted por metacognición?
Los docentes asociaron la definición de metacognición con palabras de mayor frecuencia como: proceso, conocimiento, aprendizaje, capacidad, mental, persona y situación con elementos que fueron importantes para la definición, dado que permitió inferir que para los docentes entrevistados, la metacognición la conciben como un proceso asociado a un conocimiento o aprendizaje acompañado de una capacidad mental que poseen las personas sobre una situación que realizan.
Para los docentes urbanos, la metacognición es un proceso personal que relaciona el nuevo aprendizaje con el existente; es decir, se basa en la experiencia y capacidades; con un criterio de clasificación de la distancia respuesta promedio que corresponde a 0,886.
Las respuestas que dieron los docentes rurales fueron: la metacognición es un proceso de reflexión, donde un individuo es consciente de los conocimientos, procedimientos y competencias que tiene frente al desarrollo de una situación, con un criterio de clasificación de la distancia, respuesta promedio que corresponde al 0,808.
Al analizar estas respuestas de los dos grupos de los docentes que orientan el área de matemáticas en básica primaria en los contextos urbano y rural, se pudo percibir que para los urbanos la metacognición es como un proceso personal que relaciona experiencias y capacidades existentes con un nuevo aprendizaje, mientras que para los rurales es un proceso de reflexión, donde un individuo es consciente de los conocimientos, procedimientos y competencias que tiene frente al desarrollo de una situación; se evidenció que estos docentes tienen una mayor claridad de los elementos que involucran la metacognición ya que consideran necesario la reflexión del ser humano y la conciencia de sus conocimientos, mientras que el otro grupo solo la percibía como una relación entre capacidades y conocimientos cercanos a una habilidad; no obstante, los docentes coinciden en asociar a la metacognición con procesos del ser humano o del individuo, que implica una reflexión y que está relacionada con el conocimiento o aprendizaje, pero no se evidenció la necesidad de generar regulación de sus propios conocimientos.
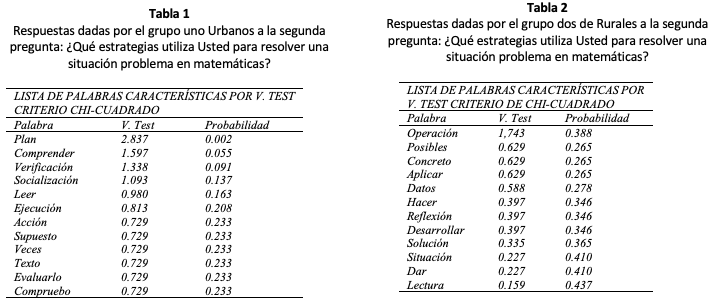
Pregunta Dos: ¿Qué estrategias utiliza Usted para resolver una situación problema en matemáticas?
Los docentes en general, asocian las estrategias empleadas en la resolución de situaciones problemas en matemáticas con las palabras: Problema, Lectura, Análisis, Datos, Respuesta, Solución, Plan, Comprensión.
Fuente: datos de la investigación
Las respuestas dadas por los docentes urbanos a la segunda pregunta fueron: leer y comprender, identificar variables, organizar datos, tener claridad en el supuesto y en la pregunta, trazar plan de acción, ejecutar el plan trazado; con un criterio de clasificación de la distancia, respuesta promedio que corresponde al 0,826.
Las respuestas dadas por los docentes Rurales a la segunda pregunta fueron: leer muy bien, extraer los datos necesarios, graficar si es necesario, identificar cual es la pregunta clave, resolver teniendo claro el tipo de operación que debo aplicar, releer el problema y mirar si lo resolví correctamente, con un criterio de clasificación de la distancia respuesta promedio que corresponde al 0,819.
Al interpretar las respuestas características dadas por los docentes urbanos a las estrategias utilizadas para resolver una situación problema en matemáticas, se evidenció que sus estrategias apuntan a la codificación, aclaración y entendimiento de la información del problema, centrándose en la lectura, toma de datos para realizar y ejecutar un plan, mientras que en el grupo rural se observó una estructura más reflexiva, ya que además de realizar la lectura, toma de datos y elaboración de un esquema, hacen un análisis de las posibles restricciones, como una realimentación de los procesos generando un monitoreo de la acción del proceso.
Al comparar la concepción de los docentes sobre las estrategias para resolucionar problemas con el desarrollo empleado por ellos al abordar situaciones problemas matemáticos desde la observación directa (diario de campo) no hay una coherencia estructurada dado que tan solo permitió percibir algunos elementos de la comprensión del problema mostrando la poco eficiencia de los procesos empleados, lo que permitió inferir que los docentes deben consolidar desde su práctica las estrategias correspondientes a las etapas de comprensión del problema, concepción de un plan, ejecución del plan y evaluación de la solución.
A continuación, se presentan los resultados y se analiza la pregunta cuatro de la entrevista:
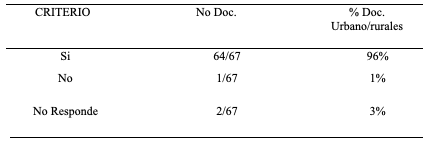
Pregunta cuatro: ¿Cuándo resoluciona un problema matemático, es consciente del proceso?
Sí_____ No_____. Justifique su respuesta
El 96% de los docentes participantes respondieron que Sí son conscientes de los procesos cuando resolucionan un problema matemático; pero al analizar los procesos realizados en el desarrollo de talleres no se evidenció un proceso de monitoreo y reflexión sobre el proceso utilizado, como tampoco una planeación, control y regulación de estos docentes; sin embargo, el 1% manifestó que no es consciente siempre y el 3% no respondió la pregunta.
Los docentes manifestaron que son conscientes cundo resolucionan problemas matemáticos asociándolo a las palabras: Proceso, Solución, Problema, Situación, Resolverlo, Respuesta, Estrategias, palabras que en primer momento no permiten percibir que la concientización está ligada a acciones de pensar, sentir, que conlleva a un proceso de reflexión y seguimiento permanente. Observe la tabla siguiente:
Tabla 3
Respuestas dadas por los docentes a la pregunta ¿Cuándo resoluciona un problema
matemático, es consciente del proceso? Sí___ No__. Justifique su respuesta
Fuente: datos de la investigación
Los docentes urbanos en sus respuestas características presentan una necesidad de comprender la situación de lo planteado e inmediatamente lo ligan a acciones como extraer información y luego, llegar a una verificación o validación de sus respuestas; los rurales manifestaron en primera instancia, que deben identificar el contexto e implícitamente ligaron a procedimientos que no son explícitos.
Se evidenció que para los docentes que orientan matemáticas el proceso de ser consiente se podría asociar al proceso de planeación donde organizan y comprenden el planteamiento del problema, centrándose en establecer procedimientos para trabajar la resolución del problema en la línea de (Pintrich, 1991).
De igual forma, se pudo asociar la habilidad de comprender, a la información para ordenar las acciones al ejecutar una tarea, elemento que se evidenció en la observación directa (diario de campo) cuando realizaron situaciones problemas en los talleres resueltos por ellos donde se mostró niveles de entendimiento, interpretación, manejo de recursos y uso de conceptos matemáticos, las cuales se aproximan a las habilidades básicas consideradas por Schoenfeld (1992), como particularizar, generalizar, descubrir patrones y relaciones, hacer conjeturas y justificar respuestas, habilidades que por sí solas no garantizan la eficacia en la resolución del problemas matemáticos.
Pregunta nueve: ¿Qué entiende por habilidad matemática?
Las palabras de mayor frecuencia empleadas por los docentes para asociarlas con habilidad matemáticas fueron: Capacidad, Situación, Resolver, Matemáticos, Problema, Solucionar, Desarrollar, Facilidad, palabras que no son dicientes ya que no abordan la definición de habilidad matemática, no presentan acciones claras a ejecutar desde una competencia de resolución de problemas; a pesar de que en su práctica docente, emplean este término con frecuencia; sin embargo, carece de claridad conceptual cuando se pregunta sobre el particular.
La respuesta de los docentes urbanos a la pregunta fue: facilidad de resolver situaciones problema, manejo del algoritmo, competencias diversas de comunicación, razonamiento matemático y facilidad de enseñar, con un criterio de clasificación de la distancia, respuesta promedio que corresponde al 0,879.
La respuesta de los docentes rurales a la pregunta fue: es la capacidad que posee una persona o individuo para desarrollar o afrontar una situación que requiera el uso de elementos matemáticos con un criterio de clasificación de la distancia, respuesta promedio que corresponde al 0,746
Los docentes urbanos en sus respuestas características hablaban de la necesidad de mostrar destrezas para resolver situaciones problema, manejo del algoritmo, competencias de comunicación y razonamiento matemático; mientras que los docentes rurales en sus respuestas características, giraban en torno a la capacidad que posee una persona o individuo para desarrollar o afrontar una situación que requiera del uso de elementos matemáticos. Ambos grupos evidencian en sus respuestas, que la habilidad matemática era la capacidad del individuo de comprender, proponer y efectuar algoritmos, así como realizar razonamientos matemáticos. De acuerdo con lo expresado por los dos grupos de docentes, se pudo inferir que las habilidades matemáticas son procesos implícitos que inducen al uso de algorítmicos pero que no son tan fáciles de definir, pareciera que, aunque es una palabra muy común en el uso pedagógico de la práctica docente, no se tienen los elementos suficientes para precisar.
Es así como los elementos: estrategias de análisis, modelar, conjeturar, uso de materiales, interpretación y representaciones no se evidenció en las respuestas características dadas por los docentes participantes en la investigación, lo que permite inferir que se hace necesario realizar un reconocimiento de los referentes de calidad en el área, para lograr consolidar procesos desde su práctica, como la visualización, representación, modelación, resolución de problemas y conjeturación de una situación abordando el conocimiento matemático en forma eficaz aproximándose más a la definición de habilidad matemática.
A continuación, se precisa un poco más sobre la resolución de problemas con habilidad, haciendo la pregunta siguiente:
Pregunta once: ¿Qué entiende Usted por Resolución de problemas matemáticos?
Los docentes en sus respuestas asocian la resolución de problemas con palabras como: Proceso, Situación, Solución, Problema, Respuesta, Diferentes, Matemáticas, Resolver, elementos que pueden ser parte; sin embargo, no se evidencia en sus respuestas características como pasos, estrategias, metacognición o cognición que son procesos fundamentales para la resolución de una situación problema, pareciera que aunque hay un uso frecuente de estas palabras no hay una apropiación de lo que significa.
La respuesta de los docentes urbanos a la pregunta fue: retomar un problema para plantear un nuevo proceso de solución ya sea que hubiese quedado mal o porque existían diferentes soluciones, con un criterio de clasificación de la distancia respuesta promedio que corresponde al 0,847.
La respuesta característica de los docentes rurales fue: es un proceso de pensamiento que permite integrar los demás procesos para el desarrollo de competencias y coloca en juego habilidades del individuo. Este proceso debe asociarse a contextos mediados y de interés para activar pre saberes y saberes nuevos con miras a la adquisición de aprendizajes significativos; con un criterio de clasificación de la distancia donde respuesta promedio de 0,794.
No se evidencia en sus respuestas características como pasos, estrategias, metacognición o cognición que son procesos fundamentales para la resolución de una situación problema, pareciera que aunque hay un uso frecuente de estas palabras no hay una apropiación de lo que significa.
Al retomar las respuestas características de los dos grupos de docentes se observó que, para los docentes urbanos resolucionar un problema está ligado a plantear un nuevo proceso de solución, ya sea que hubiese quedado mal o porque existían diferentes soluciones, mientras que para los docentes rurales es un proceso de pensamiento que permite integrar los demás procesos para el desarrollo de competencias y coloca en juego las habilidades del individuo. Consideran también, que este proceso debe asociarse a contextos mediados y de interés para activar pre saberes y saberes nuevos, con miras a la adquisición de aprendizajes significativos.
Al comparar las respuestas características de los docentes se evidenció que, para los docentes urbanos resolucionar un problema está orientado a la reformulación del mismo, ya que era considerado como un proceso no asertivo; mientras que para los docentes rurales, el resolucionar un problema presenta elementos muy valiosos y más asertivos frente al concepto, mencionan que se hace uso de conocimientos previos y nuevos, hablan de las habilidades del individuo, de pensamientos y procesos para el desarrollo de competencias; aquí hay una gran diferencia en la estructura epistemológica de los docentes mostrando un mejor conocimiento en los docentes rurales. Al comparar estas respuestas características con la observación directa (diario de campo) de los docentes cuando resolucionan situaciones problemas en los talleres se evidencia una tendencia en solo procesar información o en mirarlo como una situación que requiere un solución única, pareciera que en el lenguaje de los docentes resolucionar un problema matemático es un “eslogan” y no más, dado que no se evidenciaron estrategias claras de planeación, regulación y control, acompañados de procesos de conocimiento para monitorear y reflexionar, lo cual permite evidenciar la identificación de patrones y decidir con rapidez si la situación es un problema o un ejercicio, aplicar diversas tácticas y heurísticas, determinar la exactitud y pertinencia de los datos disponibles para abordar la tarea de forma eficaz y eficiente que son algunos de los elementos considerados por Woods (2002).
La muestra estuvo compuesta por 67 docentes en ejercicio, de básica primaria, que dictan matemáticas a sus estudiantes, en Instituciones Educativas del sector oficial, del departamento de Boyacá, Colombia.
La investigación indaga sobre las estrategias metacognitivas que emplean los docentes en la etapa de comprensión del problema, al resolucionar una situación problema.
Se consultaron teóricos como Flavell, (1979); Polya, (1954); Poggioli, (1983, 2001); Mayer (1982, 1987); Morales (2005); Stanic y Kilpatric, (1998); Ball et al (2001, 2008); Shulman, (1986), Pintrich et al, (1986, 1991, 1993) para los diferentes temas que trabajó la investigación; así como investigadores nacionales e internacionales en el estado del arte.
La investigación aborda temas como: las estrategias metacognitivas, la resolución de problemas, la fracción parte todo en contextos continuo, discreto y como razón, el conocimiento del profesor de matemáticas MKT en la habilidad de resolucionar problemas matemáticos, las habilidades de los docentes epistemológicas y pedagógicas.
Se hizo análisis textual para las respuestas de los docentes a las diferentes preguntas contenidas en los talleres y entrevista semiestructura. Fuera de estos dos instrumentos citados se trabajó el diario de campo, para la observación directa.
Se logra identificar los tipos de conocimiento específicos que se activan en los docentes en la comprensión del problema de 41 de los 67 participantes con los siguientes resultados: 21 docentes tienen conocimiento lingüístico (11 rurales y 10 urbanos); 8 docentes tienen un tipo de conocimiento semántico (4 rurales y 4 urbanos); y 12 docentes tienen un tipo de conocimiento esquemático (11 rurales y 1 urbano); 26 docentes, (24 rurales y 2 urbanos), no realizan ningún proceso o esquema frente a la resolución de la situación problema dejando en blanco la hoja, razón por la cual, no se pudo identificar su conocimiento; la no consolidación de procesos muestra un alto grado de dificultad en los docentes en las estrategias metacognitivas, como la habilidad pedagógica y epistemológica al resolucionar situaciones problemas con el uso del concepto de fracción parte – todo.
Los resultados indican que los docentes, en términos generales, no se interesan por la metacognición y sus estrategias de planeación, control y regulación, por lo tanto muestran un desconocimiento de las estructuras de las etapas de resolución de problemas y por ende, no hay habilidad en los docentes, que permita mostrar una competencia de resolución de problemas eficaces y eficientes.
Al resolucionar problemas de fracción parte - todo, lo hacen rápidamente, sin mediar procesos de reflexión; trabajan al estilo tradicional algoritmos y numéricos; se preocupan por dar la respuesta rápidamente, no planean, controlan ni regulan sus procesos y presentan bajo eficiencia.
Se presenta confusión conceptual en el uso de la fracción parte todo en contexto discreto y continuo, aunque lo ejecutan de forma mecánica no hay una conciencia clara de la diferencia entre ellos, por cuanto no logran argumentar al respecto; en el uso de la razón, presentan mayor dificultad porque no hay una comprensión en el orden de relacionar las variables, presentando una baja eficiencia en la resolución de situaciones problemas escolares.
Respecto al trabajo con la fracción parte –todo y su uso en situaciones problemas en contexto continuo, contexto discreto y como razón, se pudo constatar que tienen debilidades frente a su comprensión y por ende en el uso de resolución de situaciones problemas que implican estos conceptos, con un alto grado de falencia, a pesar de ser usados en la cotidianidad del aula, su experiencia de 15 años de enseñanza en promedio del tema, a la luz del currículo y los referentes de calidad educativa.
En términos generales, aunque los docentes manifiestan que resuelven las situaciones problemas con habilidad, en un alto porcentaje, estos procesos no los realizan en todas las situaciones problemas planteados de acuerdo a sus habilidades epistemológicas y pedagógicas con baja eficiencia y eficacia, razón por la cual no se puede hablar de procesos generales que los docentes realizan con sus estudiantes en la cotidianidad del aula, en otros términos, se debe actualizar sus prácticas docentes a la luz de los referentes de calidad educativa del país en pro del desarrollo de aprendizajes y no de contenidos, que propendan por el desarrollo de competencias matemáticas desde la resolución de problemas, para así fortalecer su praxis entendida como ese proceso reflexivo permanente desde su rol como maestro.
Se hace necesario que el docente realice un proceso meta-reflexivo desde sus prácticas y sus habilidades en la resolución de problemas que permita evidenciar el ser conscientes del proceso que emplean para resolver una situación problema, su monitoreo y reflexión sobre lo ejecutado, ser organizado y sistemático en el proceso de resolución, aplicar tácticas y procesos heurísticas que evidencien exactitud y pertinencia con los datos disponibles, elementos básicos contemplados, según Woods (2002) para resolucionar problemas matemáticos como una habilidad.
Los docentes que enseñan matemáticas están llamados a conocer las estrategias metacognitivas de Planeación donde se analiza y comprende la situación problema desde la comprensión, a través de preguntas orientadoras que permitan identificar en primera instancia el contexto (¿quién, para qué, cómo, cuándo, dónde suceden los hechos,? ), las restricciones o condiciones presentadas en la situación problema, los datos que permiten centrar el problema, y la identificación de la tarea que está orientada a reconocer lo que se quiere del problema, ligados a la comprensión literal e inferencial del texto; de Control que refleja su atención, cuestionamiento interno del docente cuando realiza su solución apoyado en la realimentación que realiza, para determinar el proceso a seguir para solucionar en forma satisfactoria la situación problema y el de Regulación que son los ajustes continuos de los procesos cognitivos, como cambios de estructuras, como borrones o tachones de algún procedimiento realizado, entre otros.
Por otra parte, se puede concluir, que los docentes rurales con formación en licenciatura de en básica primaria son más reflexivos y analíticos antes que netamente numéricos, en sus métodos presentan una mejor estructura de los procesos metacognitivos de planeación, control y regulación que los docentes urbanos licenciados en matemáticas e ingenieros, pareciera que éstos solo buscan dar una respuesta pronta de forma numérica a la situación problema pero no realizan un proceso de reflexión sobre: ¿el cómo?, ¿el cuándo? y ¿cuál es la tarea? que de manera implícita realizan los docentes rurales al buscar verificar su eficacia en la solución.
Respecto a preguntas y objetivos de la investigación se alcanzaron los objetivos propuestos y se dieron respuesta a las preguntas, a través de la investigación.
La investigación fue innovadora en la medida que los estudios sobre metacognición se han centrado a nivel de los estudiantes, pero no se han detenido en los docentes y su praxis, por lo cual resulta de vital importancia abordarlos, para comprender plenamente los procesos y habilidades que ellos poseen.
La utilidad de la presente investigación para académicos, docentes y otros sectores educativos (Instituciones Educativas, Secretarías de Educación y sectores de la sociedad educativa), radica en la trascendencia en el tiempo que pueda tener por la actualidad de la problemática abordada, el aporte de nuevas herramientas y técnicas de investigación con docentes de básica primaria, la actualización de conocimientos preexistentes sobre las diferentes temáticas abordadas y quizás lo más importante logar realizar una meta-reflexión de las prácticas de los docentes.
La investigación abre una nueva línea a trabajar desde la indagación en las prácticas de los docentes y sus competencias matemáticas desde su experiencia escolar, como también la necesidad de actualizarse desde los referentes de calidad educativa del país y el uso y comprensión de los resultados externos e internos para una evaluación formativa.
Proyección de la investigación, a futuro la investigación permitirá realizar análisis cuantitativo de información textual, utilizando TDA (topological data analysis) referencia cuyo objetivo es encontrar estructura e invariantes topológica de gran cantidad de informe textual, estructura jerárquica de los datos y otros.
Ball, T.et al., (2008)Content Knowledge ForTeaching: What Makes It Special Journal Of Teacher Education. 9 Abr. 2015 Recuperado de: Http://Jte.Sagepub. Com/Content/59/5/389.
Bañuelos, A.M. (1995). Resolución de Problemas matemáticos en estudiantes de bachillerato. Perfiles Educativos. No.67, p.50-58.
Castro, E. (2015) Significados de las Fracciones en las Matemáticas Escolares y Formación inicial de maestros”, tesis doctoral.
Dijkstra, S. (1991). Instructional design models and the representation of knowledge and skills. Educational Technology, 31, (6), p.19-26.
Flavell, J. (1979). Metacognitive aspects of problem solving. En Resnick, L. (Ed.). The nature of intelligence. Hillsdale: LEA.
Iriarte, P. (2011). Estrategias Metacognitivas en la Resolución de Problemas Matemáticos, en Estudiantes de 5º de Básica Primaria. Universidad De Sucre. I.E. Normal Superior De Sincelejo. Colombia.
Lago de F. Gamboa A. y Montes A. (2013). La Educación Básica en Colombia: Una mirada a las políticas educativas: Revista Saber, Ciencia y Libertad. Universidad Libre. ISSN 2382-3240. Alpha Editores. Volumen 8 No. 2. Pgs. 146-147.
Llinares, S. y Sánchez (1981). Fracciones. Madrid.
Llinares, S. y Sánchez (1997) Aprender a Enseñar. Modos de Representación y Numeros Naturales. Madrid.
Llinares S. y Sánchez (2004). Fracciones. La relación Parte –Todo. Madrid, E. Síntesis.
Mayer, R. (1983) Pensamiento, Resolución de Problemas y Cognición.
Ministerio de Educación Nacional MEN. (2006). Estándares Básicos de Competencias en Matemáticas. Bogotá D.C.: Escribe y Edita
MEN. (2013. 2014, 2015, 2016). Resultados Pruebas Saber. Bogotá. Colombia
MEN. (2013). Evaluación de Competencias. Bogotá, Colombia
MEN. (2002) Estatuto de Profesionalización Docente. Bogotá, Colombia.
MEN. (2015) Matrices de referencia. Bogotá, Colombia.
Morales J., D.J., (2008). Estrategias que se tipifican en estudiantes, que utilizan tipos diferentes de representación de conocimiento: lingüísticos, semántico, esquemático en la resolución de problemas. De razón de cambio. Universidad Pedagógica Nacional.
Obando, G. (2003). La Enseñanza de los Números Racionales a Partir de la Relación Parte-Todo. Revista Ema, 8(2), 157-182
Ordoñez, C. ( 2012) La Fracción, elemento Dialogante en el Contexto Matemático. Tesis de maestría. Universidad Nacional de Colombia. Bogotá, Colombia
Pintrich et al., (1986). Teaching And Learning. In The College Classroom: A Review Of The Literatura. Ann Arbor: University Of Michigan, National Center For Research To Improve
Pintrich, P. y García, T. (1993). Student Goal Orientation And Self Regulation In The College Classroom. En: M.L. Maher Y P.R. Pintrich (Eds.) Advances In Motivation And Achievement. Greenwich, Ct:Jai Press.
Polya, G. (1957) Mathematics And Plausible Reasoning. (Vol. 1,2). Princeton. Princeton University Press.
Pontón, L. (2008) Una Propuesta Multirregistro para la Conceptualización Inicial de las Fracciones. Tesis De Maestría. Universidad Del Valle. Instituto De Educación Y Pedagogía. Grupo De Educación Matemática. Cali. Pp.294.
Poggioli, L. (1983). Enseñando a Aprender. Estrategias de Resolución de Problemas.
Poggioli, L. (1987) Serie: Enseñando a Aprender. Estrategias de Resolución de Problemas. Recuperado en: Http://Www.Fpolar.Org.Ve/Poggioli/Poggio1ref.Htm.P.1
Shoenfeld, A. (1992) Learning To Think Mathematically Problem Solving Metacognition And Sense Making In Mathematics. In Handbook For Research On Mathematics Teaching And Learning. New York: Mcmillan.
Shulman, L. (1986). Those Who Understand: Knowledge Growth in Teaching. Educational Researcher. Vol. 15, No. 2, 4-14.
Stanic, G. y Kilpatrick, J.(1989). Historical Perspectives On Problem Solving In The Mathematics Curriculum. In R. Charles&Silver (Eds.) The Teaching And Assesing Of Mathematical Problem Solving, Pp.1-22 Reston, Va: National Council Of Teachers Of Mathematics.
Villanova, S. et al. (2005). La Educación Matemática. El Papel de la Resolución de Problemas en el Aprendizaje. Universidad Nacional De Mar Del Plata, Argentina. Recuperado en: Http:/Www.Campus-Oei.Org/Revista/Delos Lectores/203vilanova.Pdf
Weinstein, C. y Mayer, R.E. (1986), The Teaching Of Learning Strategies. En: M.C. Wittrock M.C. (Ed) Handbook Of Research On Teaching.New York: Mcmillan.
Woods (2002). ABC. Of Learning And Teaching In Medicine: Problem Based Learning. Bmj. February 8; 326(7384): 328–330.
1. Estudiante Doctorado en Ciencias de la Educación Rudecolombia cade Tunja. Universidad Pedagógica y Tecnológica de Colombia. Formadora del Programa Todos a Aprender del Ministerio de Educación Nacional Colombia. Correo electrónico de contacto: dojemoja@gmail.com