

 Vol. 39 (Number 38) Year 2018. Page 8
Vol. 39 (Number 38) Year 2018. Page 8
Galina A. DUBININA 1; Irina K. STEPANYAN 2; Elena V. GANINA 3
Received: 17/04/2018 • Approved: 01/06/2018
ABSTRACT: This paper gives insight into the trilateral activity of the instructors in Higher Mathematics, English as a Foreign Language, and Russian, as the language of the host country, aimed at providing entrant international students with a preparatory course of Higher Mathematics. Authors show how the curriculum is structured with a view to a large diversity in the initial level of mathematical skills. Another challenge is the choice of the languages to be used in training. The article infers that close cooperation between the instructors in mathematics, English and Russian, contributes to students’ progress. Some statistical data are given to show who the students are, what their educational background is, and what their progress should be so that they could successfully join the first year students of the University. The choice of dual language educational activity and the need for both mathematics and foreign language propedeutics is given thought to. |
RESUMEN: Este documento da una idea de la actividad trilateral de los instructores en Matemáticas Superiores, Inglés como Lengua Extranjera, y Ruso, como el idioma del país de acogida, destinado a proporcionar a los estudiantes internacionales con un curso preparatorio de Matemáticas Superiores. Los autores muestran cómo se estructura el plan de estudios con miras a una gran diversidad en el nivel inicial de habilidades matemáticas. Otro desafío es la elección de los idiomas que se utilizarán en el entrenamiento. El artículo infiere que la estrecha cooperación entre los instructores en matemáticas, inglés y ruso contribuye al progreso de los estudiantes. Se proporcionan algunos datos estadísticos para mostrar quiénes son los estudiantes, cuál es su formación académica y cuál debe ser su progreso para poder unirse con éxito a los estudiantes de primer año de la Universidad. Se reflexiona sobre la elección de la actividad educativa en dos idiomas y la necesidad tanto de matemática como de propedéutica en el idioma extranjero. |
There has been a lot of debate lately on dual language instruction in which students master academic disciplines, whose content is taught and assessed in two languages. Thus the educator in a special discipline instructs students in two languages, normally English as the language of international communication and the native language. Dual language instruction is also widely used when it concerns teaching international students. In this situation English is combined with the language of the host country. Nowadays team teaching has become very popular due to the efficiency of such a technology. Language training tends to be more and more content oriented on the one hand and on the other hand the higher scope of academic mobility has called for multidisciplinary approach in academic education, especially, when it concerns multilingual professionally oriented training in special disciplines. This paper is based on the experience of dual language instruction at the preliminary course for international students of the Financial University under the Government of the Russian Federation.
Like any other disputable point, the idea of dual language instruction, or dual immersion programs, or two-way immersion had various interpretations. Initially it meant a form of education in which students were taught literacy and content in two languages and referred to bilingual environment and the field of early childhood education (Meier 2010). Research of William Steven Barnett and others (2007) showed that children in dual language programs experience academic gains, including gains in early literacy skills, comparable to those of children in English-only programs. Later the focus moved to dual language instruction at universities where international students experience foreign language immersion. In the USA, particularly for the areas with a lot of Spanish native speakers, the Guiding Principles for Dual Language Education (http://www.cal.org/resource-center/publications/guiding-principles) were developed. They offered dual language programs describing possible levels of alignment: minimal alignment, partial alignment, full alignment, etc. (Howard et al. 2007). The most frequent point to be discussed is the amount of time spent in the partner language. Some research indicates that students who spend more time in the partner language do better in that language (Lindholm-Leary 2008; Lindholm-Leary 2014). Leo Gomez (2005) notes that in areas with a high number of English Language Learners (ELL) a 50/50 model is more appropriate. The model also divides the language use by content area and by time. The partner language and English are used equally in the later grades, but at initial stages a 90/10 model may be used. In some cases special classes are offered in the partner language. LSP (Language for Specific Purposes) performance assessment has become a special focus lately and instructors argued over testing tools and processes trying to find how assessment could be done more accurately and more validly (Lockwood 2015). Some educators in the USA indicate that the increasing quantity of immigrants who speak a different language at home put up relatively poor Math performance. They come to the conclusion that mathematics is not as language-dependent as other disciplines. Many English language learners (ELLs) will excel in mathematics because it is a "universal language" and students may have had prior educational experience in it (Robertson 2010; Stepanyan 2017). Never-the-less dual language immersion training in Mathematics should gradually bring students to the use of mathematical apparatus in dealing with the integrated, practice-oriented tasks (Konnova, Rylov and Stepanyan 2016a). Our practical experience leads to the same assumption.
Dual-language instruction has gained attention recently in regard to providing students with better organized content-oriented workshops, offering students more choice, exposing students to wider scope of sources in partner languages. One of the most efficient methods based on language immersion is known to be Content and Language Integrated Learning (CLIL), i.e. learning content through an additional language (or languages). Moreover, in the process of studying an academic discipline, working the assignments, discussing the ins and outs of the subject with other international students, new linguistic competencies develop.
International students in their elementary/preparatory courses with dual-language instruction demonstrate higher academic performance than their peers in single language training. An integrative approach to the mathematical preparation of the international students requires close interaction between an instructor of a special discipline (mathematics), a teacher of a foreign language, and a teacher of the language of a host country, which allows such a team to organize training in the context of the particular discipline. Furthermore, this tendency appears to be efficient when it concerns training students at the faculties providing instruction in English as a foreign language.
The statistical preamble below accounts for the choice of methodology and techniques to be used in educational activity under discussion (Dubinina, Stepanian 2016).
As research displays, some students know English well enough to study in English, but lack mathematical skills and the knowledge of terminology. Other students know the language of the host country, but not enough to study mathematics in it. There are still others, who know neither English nor the Language of the host country, in the situation under discussion it is the Russian Language (Fig. 1).
Figure 1
Knowledge of Mathematics, English and Russian.
(Preparatory faculty, entrant international students 2016)
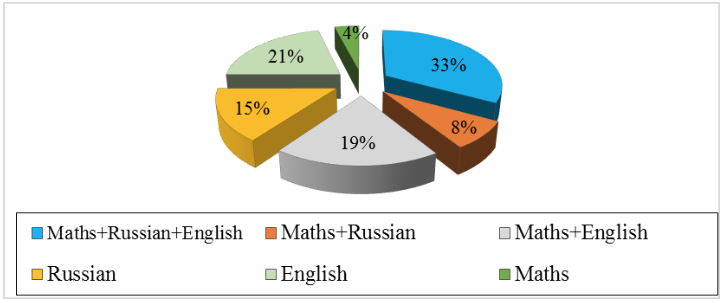
Thus, 33 % of the students have quite a sufficient level of both Mathematics, English and Russian which allows them to master the Bachelor programme. Unfortunately 36 % of students are not good at mathematics, and this seriously aggravates the situation. Moreover, 4% of the entrant students while being quite good at mathematics do not know either English or Russian.
It should be noted that limited-English/Russian-proficient students have to meet the same state-required learning standards as native students, that’s why dual-language education has significant implications for how international students are taught.
It’s common knowledge that mathematics as the Financial University’s basic discipline presents the highest scope of challenges for its learners. It should be noted that students from different countries have a very uneven level of mathematical skills and this accounts for the necessity of a preparatory course.
At the first lesson in mathematics, a diagnostic test is usually carried out in order to have the input level of knowledge in mathematics assessed. A short investigation starts with a basic math problem in which the student can demonstrate how he or she has mastered the basic concepts and skills.
You can see the results in the diagram below (Table 1).
Table 1
Assessment of the Initial Level of Mathematics
Points: |
Number of students |
% |
7-9 |
8 |
15% |
4-6 |
9 |
17% |
3-5 |
11 |
21% |
0-2 |
24 (13)* |
47% (25%)* |
Total: |
52 |
100 % |
* The number of students with the zero level is given in brackets.
Below goes the detailed description of the workshop on preparatory course in mathematics and the explanation why it has been structured in that particular way (Table 2).
Table 2
Contents of the course in Higher Mathematics for Preparatory International Students
Contents |
Didactic Units |
1.Real numbers and operations on them |
Numerical sets. Natural, integer, rational and real numbers. The numerical line, the intervals and their notation, the simplest inequalities and their systems. The number module, the geometric meaning of the module. Numerical laws and formulas for reduced multiplication. Newton's binomial and Pascal's triangle. The concept of identity. Identical transformations of numerical and algebraic expressions. |
2. Function and its properties |
The concept of a function, a domain of definition, a range of values. Function’s zeros, intervals of constant sign, increasing, decreasing and extremes of the function, largest and smallest value, parity / oddness, periodicity. Graph of function. |
3. Linear function |
Direct, the dependence of its position on the coefficients. Solution of linear equations and their systems. Different ways of solving: graphical, substitution, addition. Solution of linear equations and systems of linear equations with parameters. Solution of systems of linear equations by the Gauss method. Linear inequalities and their systems. |
4. Quadratic function |
Parabola and its properties. Movement of graphs. The vertex of the parabola. Graphical solution of quadratic equations and their systems. Discriminant and roots of the quadratic equation. Vieta's theorem. Solution of quadratic equations with parameters. Decomposition of a square trinomial into multipliers. Solutions of quadratic inequalities by the interval method. |
5. Module number |
Function and its properties. Graphs of functions , and . Solution of equations and inequalities with modulus. |
6.The inverse proportionality function |
Function and its properties. The concept of an asymptote. Graphs of functions , , , . Fractional-rational equations, selection of roots. Method of intervals for solving fractional-rational inequalities. |
7. Square root |
Function and its properties. Solution of irrational equations graphically. The solution of irrational equations. Irrational inequalities. |
8. Power function |
Functions and . The concept of a complex and inverse function. Solution of algebraic equations. Horner's scheme. |
9. Exponential function |
Function , its properties and graph. Transformations of exponential expressions. Equations and inequalities with exponential expressions. |
10.The concept of the logarithm |
Calculation of logarithms and transformation of expressions with logarithms. Logarithmic function, its properties and graph. Logarithmic equations and inequalities. Systems of equations with logarithms. |
11.Trigonometry |
Sine, cosine, tangent and cotangent of the acute angle of a right triangle. Basic trigonometric identity. Table values of trigonometric functions. Trigonometer, sine and cosine of the angle as coordinates of a point of a circle with unit radius. Functions , , , , and their properties. Motion of graphs of trigonometric functions. Trigonometric formulas for the double angle, degree reduction. The formulas for the transition from sum to product |
12.Trigonometric equations |
Trigonometric equations: the simplest, reducible to square, factorizable. |
13.The concept of a derivative of a function |
Derivative of a function. Table of derivative formulas. Rules of differentiation of sums, differences, products, and quotients. Derivative from geometric point of view. Tangent line to the graph of a function. Criteria for monotone functions. Sufficient condition for local extremum. The first derivative test. |
14.The concept of the integral |
A table of integrals for elementary functions. Indefinite integral and its properties. Linear replacement in an indefinite integral. A definite integral and its geometric meaning. The Newton-Leibniz formula for a definite integral. |
15. Arithmetic and geometric sequences |
Arithmetic progression: definition, methods of assignment, the formula of the nth term and the partial sum. Geometric progression: definition, methods of assignment, the formula of the nth term and the partial sum. The sum of an infinitely decreasing geometric progression. |
16. Vectors in geometric and coordinate interpretation |
Operations on vectors: addition of vectors, multiplication of a vector by a number. Scalar product of vectors, length of a segment. Formulas of the middle point of a segment. |
The system of mathematical notation used at the preliminary course is a genuinely international language. Mathematical training is seen not as a description of the external world of reality, not merely as a tool for studying such a world.
The first section of the course begins with the definition of numerical sets, then the concepts of natural, integer, rational, and real numbers are refined. The concept of complex numbers is familiar to some students from the course of mathematics at a national school, so the instructor mentions this expansion of the concept of number, noting that the study of complex numbers will not be covered by the program of the preparatory course, but will be studied in the course of Higher Mathematics. The next item to be introduced is the notion of a numerical line, the modulus of a number as the distance from a zero point to a given number. The second part of the section is devoted to numerical and algebraic expressions, formulas of reduced multiplication, identical transformation of various expressions. As a rule, the initial level of students allows the instructor to work out such a large amount of didactic units in 6-8 academic hours.
The second section introduces the concept of a function without an exact mathematical definition. Such didactic units as function zeros, intervals of a constant sign, increase / decrease and extremums of a function, the largest and smallest value of a function on an interval, elementary functions and their graphs are considered. Tasks that are solved in this section do not imply the use of a derivative, and the definitions correspond to the level of the secondary school.
The following 10 sections successively consider different types of functions, methods for solving the corresponding equations, inequalities, and their systems. Let's list the sections and the corresponding didactic units.
Thus, the first 12 sections are based on the knowledge obtained by the students at national schools and do not imply the deepening of this knowledge, but are aimed primarily at studying mathematical terminology in Russian, perceiving the structure of the course of mathematics at Russian educational institutions, getting ready for the future study of Higher Mathematics.
The last four sections of the course, from 13 to 16, are the most important for mastering the university course in Higher Mathematics. Differential and integral calculus are crucial in the first year of the university, regardless of the direction of preparation. The sections "Numerical Sequences" and "Vectors" are more additional for the course in question than not, but they are important for mastering such topics of Higher Mathematics as "Rows", "Linear Algebra" and "Analytical Geometry" respectively.
Most sections of the course suggest the so-called functional approach: the current topic begins with the definition of the function, its properties, and the construction of graphs. Next, different types of equations and techniques for solving them are considered. The section ends with the solution of the corresponding inequalities and problems with the advanced level of complexity.
It is important to prepare listeners for the perception of a large amount of oral information during the lecture, to teach not only to decide, but also to correctly explain the solution of assignments (Konnova, Rylov and Stepanyan 2016b).
While developing mathematical terminology students encounter problems caused by the specificity of training in mathematics at national schools. At the preparatory course educators should get their students acquainted with the interdependence between Russian and national approach to solving different mathematical problems, especially when it concerns tasks for the students with the advanced level of mathematical training. However, sometimes tasks with elementary for the Russian students level of complexity cause difficulties for the leavers of national schools. To reach better understanding and greater efficiency in training such a diverse group of students, dual language instruction is of paramount importance.
The next point to be considered is linguistic support which is based on the terminology envisaged by the Act of the Ministry of Education and Science of the Russian Federation “On the approval of the requirements for the development of additional general education programs that provide training for foreign citizens and stateless persons to develop professional educational programs in Russian” by the direction Economics and Management (Rossiiskaia Gazeta 03.12.2014). It is of bilingual nature, the underlying reason for which is the statistics given below (Figure 2) which concerns the initial level of English and Russian.
Figure 2
Knowledge of Foreign Language
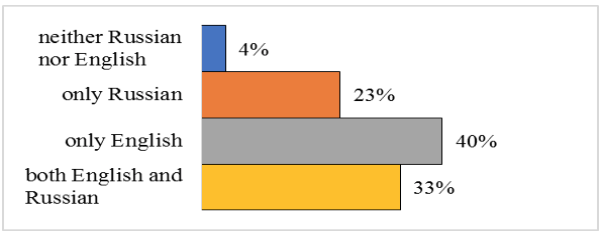
Another item is worth mentioning: the language of mathematics consists mostly of signs and symbols and is carefully and purposefully designed. It is precise, concise and one and the same all over the world, though the people of different countries convert it into their particular spoken language. Moreover, the language of mathematics is really cross-disciplinary, it is used not only in Economics, but also in other disciplines, including statistics, risk analyses, investment management, and even philosophy, linguistics, poetry and music. Mathematics supplies a language for the treatment of the qualitative problems of various sciences.
For foreign students, whose knowledge of the Russian language is insufficient, Russian turns out to be part of the educational process and the primary means of professional orientation. Moreover, for foreign students of the Russian language educational and professional activity dominates in the hierarchy of motives, which makes it obvious that the Language for Specific Purposes (LSP), namely Finance and Economics, insures a foreign student’s mastery of the university course, progress at the examinations and ability to gain professional competence in the chosen field. (Bezhаnovа, Gаninа 2010)
The preparatory faculty of the Financial University under the Government of the Russian Federation trains students at three levels of Russian: elementary, basic and advanced (students from the CIS - Tajikistan and Uzbekistan). Nevertheless, at the lectures and seminars /workshops in mathematics the groups are mixed, i.e. elementary students study with students at the basic or even advanced level.
Below are the statistics on the initial level of Russian (Table 3). The respondents are the focus group of 52 foreign beginner-students on their preparatory course.
Table 3
Assessment of the Initial Level of Russian
Level of Russian |
Number of students |
% |
Elementary |
36 |
70% |
Basic |
10 |
18% |
Advanced |
6 |
12% |
The course of Russian at the preparatory faculty is an initial mathematics-oriented course of the foreign language for specific purposes containing the carefully chosen Russian language backing for the course of Higher Mathematics in Russian at the Bachelor programme.
The goal of this course is to build the required scope of student’s mathematical competence in another language and teach foreign students to:
- read and understand the symbolic entries of mathematical sentences in Russian;
- understand sounding and written text in mathematics;
- briefly record the required information from paper and audio texts;
- take part in dialogues (teacher-student) and produce small monologues on the topics pertaining mathematics;
- describe mathematical notations, changes, calculations.
All the mentioned activity is supposed to ensure the ability of the students to study at the main faculties of the University together with native speakers. In some cases the graduates of the preparatory faculty enter the International Financial Faculty where all the disciplines are taught in English.
It makes sense when studying a foreign language for academic or specific purposes, be it Russian or English, takes not less than 80% of all the time spent on a foreign language course.
The communicative approach to learning demands that foreign language training for the particular professional field should be carried out within the framework of this array of scientific knowledge. No doubt, professionally oriented language training process should avoid substituting professional training itself as its ultimate goal is the formation of Foreign students’ language competence, which should allow them to study materials on special disciplines, listen to the lectures, participate at the workshops, take part in case-analyses, carry out written and oral assignments.
Planning dual language instruction in mathematics results in a combination of three components:
The analysis of the textbooks in various academic disciplines should identify the most frequent and commonly used lexical units, programs on Russian language and English language training for foreign students should be compiled on the linguistic basis aimed at forming basic subject-matter competences. It’s of paramount importance that dictionaries, glossaries, phrase-books and thesauruses are available in both languages. (Bezhаnovа, Gаninа 2013).
The peculiarity of the situation lies in the fact that the formation of the subject-matter competence is split into two spheres of responsibility: the instructor in Mathematics is responsible for the subject-matter competence, while language teachers focus on forming the communicative competence. This separation is traditional, and it takes much effort to coordinate trilateral educational activity, harmonize the curricula, establish interdisciplinary links and ensure continuity.
However, two challenging points should be mentioned.
It’s an open secret that foreign students have difficulty in mastering mathematics and, say, accounting for different reasons. It is important to indicate sections of mathematics that cannot be mastered appropriately due to the poor knowledge either of Russian or the English language. It is done by means of questioning both instructors and students. Needs analysis is the underlying basis for efficient dual language instruction. The ESP focal point is that international students are not taught English as a subject separated from the students' real world (or wishes); instead, it is integrated into a subject matter area (mathematics) important to the learners.
Mathematics like any Language for Specific Purposes (LSP) has its own vocabulary, terminology and special names. We suggest that international students study the General (Ethnic) Language in proportion 20% of the teaching time to 80% of the teaching time for the LSP.
The course of Russian as a language of the host country includes the basic mathematical vocabulary and syntactic constructions of the Introductory course on Mathematics. All the mathematical vocabulary studied at the Russian Language seminars is actively used by students not only at the stage of pre-university preparation, but also studying Higher Mathematics at the main faculties of the Financial University.
While some of the graduates of the preparatory course enter universities other than the Financial University under the Government of the Russian Federation, most of them enroll for its International Financial Faculty. Thus its educational activity may provide an illustration to the mentioned above.
The curriculum of the Faculty encompasses many economic and mathematical disciplines within the basic and specialized training sections and numerous special courses in Finance. All the academic disciplines are taught in English. The special professional training section of the curriculum offers courses in International Accounting Standards, International and Financial Accounting, Auditing, World Finance, International Corporate Finance, Corporate Business, Law and Taxation. It's evident that all these disciplines require a sufficient knowledge of Mathematics and free use of mathematical tools. Most of the students are non-Russian residents and it’s an obligatory requirement that all the Russian students have the level of English which allows them to master all the disciplines in English. Another challenge is that students from the countries other than Russia sometimes have an insufficient knowledge of English. In this situation, they are provided with extra classes of English. More often than not English remains the main language of communication. The graduates of the International Financial Faculty participate in an exchange program with the British and American universities and have their work experience gained when doing a work placement in international companies.
A math instructor engaged in bilingual programs knows how big a role the English language plays in math instruction, especially for students who come from non-English-speaking backgrounds, who are not proficient in English, and who require language instruction. This is where cooperation between educators or even team-teaching is required. English Language textbooks for Economics and Finance, used at the Financial University contain units, specializing in mathematics: “Wording Mathematical Formulae” and “Starting Linear Algebra” (Dubinina et al. 2018a; Dubinina et al. 2018b).
Never-the-less for many instructors, bringing language and math instruction together is a challenge. (Dubinina 2014). ELL teachers support instruction in the math classroom, and many math teachers who are far from being language instructors provide math instruction in English. At an ELL workshop the instructor provides students with understanding math vocabulary and it will offer them ample opportunities to use it in solving problems, following instructions, and using mathematical vocabulary correctly. As a result the students:
- will understand the content better;
- have more opportunities to clarify the difficult points;
- will be able to work together to find creative ways to solve math problems;
- will be more comfortable with Mathematics.
As incentives for Two-Way Immersion may be mentioned academic gains, English acquisition for ELL students, career readiness for, success on standardized testing and in international Case Championships. The free use of mathematical terminology in English would allow students to use information resources in case analyses and related decision making more efficiently (Dubinina, Pashtova, Stepanian 2017; Nikolaev 2016).
Yet another challenge at dual-language workshops is progress evaluation and assessment of students’ performance. No doubt, collaborative teaching integrates the strengths of multiple instructors and supplies mathematical training with linguistic support. In the situation under discussion the instructor in mathematics inevitably experiences the insufficiency of either Russian or English Language ability in regard to students’ educational activity. A comprehensive, balanced assessment is a combination of several factors.
Authors suggest applying two-dimensional assessment strategies: criterion-referenced assessment for subject-matter (mathematical) competence and either holistic or criterion-referenced approach for assessing the language ability. (Stepanyan et al. 2017)
In the course of mathematical preparation a student should be able to deliver the message, applying basic concepts, principles and formulas of mathematics, thereby proving that s/he has deeply mastered the theory and the practical use of mathematical apparatus and mathematical tools of different levels of complexity are used.
The foundation of mathematical assessment revolves around evaluating a student’s ability to apply what they have learned in mathematics to a “real world” context. In assessing learning mathematics, the followings should be emphasized.
1) Understanding of basic concepts, principles and formulas of mathematics.
2) Skills to use and represent mathematical terminologies and symbols.
3) Ability to solve the problems with mathematical thinking using mathematical knowledge and skills.
4) Ability to observe and analyze phenomena related to real life situations.
The instructor in mathematics evaluates how their students approach the problems and how much mathematical knowledge and at what level students use when solving the problems. The maths instructor also assesses how students think in the process of learning or problem solving.
Instruction typically does not include straight translation from language to language. International students in dual-language programs are generally required to meet the same learning standards and graduation requirements as other students.
In a math course dual-education students may be assessed either in English or in Russian. They may also be given various testing accommodations, such as bilingual dictionaries or additional time to complete a test.
Suggestions to achieve more accurate and more valid assessment include discourse analyses of the relevant mathematical tasks; and an instructor in mathematics as a subject matter expert (SME) is sometimes invited to the language workshop as an informant when defining ‘successful’ communication. LSP performance may be given a holistic assessment, e.g. performance may be attested as ‘weak’ and ‘strong’. Unfortunately, there is no clear line of distinction between these two marks. (Lockwood 2015)
Holistic assessment of Russian/English language ability at the dual language workshop focuses on the assessment of whole communicative activity rather than specific elements of it.
Positive assessment (“strong”) – clear message, coherent discourse, topical vocabulary, perfect cohesion, correct grammar.
Negative assessment (“weak”) – the message is non-recognizable because grammars errors and poor lexis make comprehension difficult.
Criterion-referenced assessment is more precise and matter of fact. Below is the Assessment Table based on research made by Jane Lockwood (2015).
Table 4
Assessment Table of Russian/English language ability
Criteria |
Out of 100% |
Focus |
Pronunciation |
25 % |
This domain poses the question as to whether the student is comprehensible and is using the prosodic features to deliver the message appropriately |
Lexico-grammatical choices |
25% |
This domain poses the question as to whether the choice in the Grammar and Vocabulary is of a sufficient range for the communication task and whether the errors in grammar are systemetic and posing a threat to understanding. |
Discourse capability |
25% |
This domain poses the question as to whether the student is able to deliver the message, applying basic concepts, principles and formulas of mathematics |
Interactional and strategic capability |
25% |
This domain poses the question as to whether the student is able to build a relationship and interact effectively with the interlocutor, be it a teacher or peers |
The objective of measuring language performance in oral interaction is testing oral ability. Oral ability of the students should be scored validly and reliably. Items to be also scored are: expression (attitudes, opinions), manipulation (directions, instructions, persuading, advising, warning), eliciting (information, clarification, explanation), narrating (presenting own point of view) (Stepanian, Dubinina, Ganina 2017).
No doubt, the given type of training in a foreign language (English) supplemented by the language of the host country requires a close collaboration between an instructor in mathematics and the language instructor. As a result the students will understand the content better, will be able to work together to find creative ways to solve math problems, may discuss mathematics more and will be more comfortable with mathematics.
As practical experience shows, while teaching foreign students Mathematics an instructor encounters difficulties both of the educational and cognitive nature. They are:
- the language barrier;
- differences in educational systems and the organization of educational processes;
- differences in the methodology of teaching mathematics.
Thus, benefits of bilingualism are evident both in content areas as well as in general cognitive development. Dual language instruction has proved to be the most suitable and advantageous solution in training international students with not only the different level of knowledge in mathematics but also different languages of communication. We may conclude that the interdisciplinary interaction of educational knowledge where a student develops both the professional area content and foreign language competence proves to be most efficient.
Rossiiskaia Gazeta [Ros. Gaz.] 03.12.2014, No. 275 (Russ.).
Barnett W., Yarosz D., Thomas J., Jung K. and Blanco D. (2007). Two-way and monolingual English immersion in preschool education: An experimental comparison. Early Childhood Research Quarterly, 22, 277-293.
Bezhаnovа S.V. and Gаninа E.V. (2011). Osnovy obucheniya pis'mennoj i ustnoj rechi inostrannykh studentov v ehkonomicheskom vuze (pp. 295-301). [The basis for training in written and spoken language international students at the economic university] In: Russkij yazyk v kommunikativnom prostranstve sovremennogo mira [Russian in the communicative space of the modern world], Moscow.
Bezhаnovа S.V. and Gаninа E.V. (2013). Metodicheskie osnovy vzaimodejstviya kafedry "Russkij yazyk"s kafedrami professional'nykh tsiklov Finuniversiteta (pp.34-37). [Methodical bases of interaction between "Russian language" department and professional cycle departments of the Financial University] In: Prepodavanie inostrannykh yazykov v usloviyakh internatsionalizatsii obrazovaniya. [Teaching foreign languages in the context of the internationalization of education]. Minsk: BGJeU.
Dubinina G. (2014). Organizatsiya prepodavaniya uchebnih discipline na inostrannom yasike. [Organization of teaching academic subjects in a foreign language]. In: Moscow State Linguistic University Bulletin, 12(698), 158-165.
Dubinina G. and Stepanian I. (2016). Obespechenie disciplin matematicheskogo tsicla dlya napravleniy “ekonomica” i “menedgment” inoyasichnoy poddergkoi [Providing disciplines of mathematical cycle for Economics and Management with a foreign language support]. Standarti i monitoring v vischem obrazovanii [Standards and monitoring for education], 4(3), 52-56.
Dubinina G., Pashtova L., Stepanian I. (2017). Interdisciplinary cooperation in case studies on corporate finance in a foreign language. International Research Journal, 01(55) Part 3, 30-32.
Dubinina, G., Drachinskaya, I., Kondrakhina, N., Petrova, O. (2018a). English: Economics and Finance: Part 1. Threshold. Textbook. Moscow: KnoRus.
Dubinina, G., Drachinskaya, I., Kondrakhina, N., Petrova, O. (2018b). English: Economics and Finance; Part 2. Overview. Textbook. Moscow: KnoRus.
Gomez L., Freema, D., Freeman Y. (2005). Dual Language Education: A Promising 50-50 Model. Bilingual Research Journal, 1, 145-164.
Howard E.R., Sugarman J., Christian D., Lindholm-Leary K.J. and Rogers D. (2007). Guiding principles for dual language education (2nd ed.). Washington, DC: Center for Applied Linguistics.
Konnova L., Rylov A. and Stepanyan I. (2016a). Ekonomicheskie prilozheniya vysshej matematiki v kejsah: uchebnoe posobie [Economic applications of higher mathematics in case studies: a tutorial]. Moscow: Financial University.
Konnova L., Rylov A. and Stepanyan I. (2016b).Elementy integrativnogo podhoda k bazovoj podgotovke ehkonomistov [Elements of integrative approach to basic mathematical training of economists]. Financial University Bulletin, 5, 158-166.
Lindholm-Leary K. (2014). Bilingual and biliteracy skills in young Spanish-speaking low-income children. International Journal of Bilingual Education and Bilingualism, 17(2), 144-159.
Lindholm-Leary K. and Howard E. (2008). Language development and academic achievement in two-way immersion programs. In: T. W. Fortune & D. J. Tedick (Eds.), Pathways to Multilingualism: Evolving Perspectives on Immersion Education. Oxford, UK: Blackwell, pp. 177-200.
Lockwood Jane E. (2015). Language for Specific Purpose (LSP) performance assessment in Asian call centres: strong and weak definitions. Language Testing in Asia, 5, 3.
Meier, G. (2010). Two-way immersion education in Germany: Bridging the linguistic gap. International Journal of Bilingual Education and Bilingualism, 13(4), 419-437.
Nikolaev D. (2016). Mezhdisciplinarnoe sotrudnichestvo pri ispol'zovanii kejsov po discipline “Analiz i ocenka riskov” [Interdisciplinary interaction in case application on disciplines such as “Risk Analysis and Risk Assessment”]. Materials of the International Scientific and Methodological Conference, 2017. St. Petersburg: Publishing house of Polytechnic University, pp. 81-83.
Robertson K. (2017). Math Instruction for English Language Learners. Retrieved from http://www.colorincolorado.org/article/math-instruction-english-language-learners
Stepanian I. (2017). Osobennosti prepodavaniya matematiki dlya slushatelej – inostrancev na podgotovitel'nom fakul'tete Finansovogo universiteta [Features of teaching mathematics for foreign students at the Preparatory Department of the Financial University]. In: Materials of the International School-Conference on March 27-30, 2017. St. Petersburg: Publishing house of Polytechnic University, pp. 181-182.
Stepanian I., Dubinina G. and Ganina E. (2017). Bilingvalnyj podxod k-obucheniyu matematike inostrannyh studentov [Bilingual approach to teaching mathematics to foreign students] In: International Research Journal, 12(66).
Stepanyan I.K., Dubinina G.A., Nikolaev D.A., Kapranova L.D. and Pashtova L.G. (2017). Cross-disciplinary case-analyses of investment optimization in a foreign language applying dynamic programming. Espacios, 38(62), 19.
1. Financial University under the Government of the Russian Federation, Leningradsky Prospect 49, 125993 Moscow, Russia. E-mail: galina.a.ru@mail.ru , gadubinina@fa.ru
2. Financial University under the Government of the Russian Federation, Leningradsky Prospect 49, 125993 Moscow, Russia. E-mail: fpk0701@mail.ru , ikstepanyan@fa.ru
3. Financial University under the Government of the Russian Federation, Leningradsky Prospect 49, 125993 Moscow, Russia. E-mail: el.ganina2012@yandex.ru , eganina@fa.ru