

Vol. 39 (Nº 33) Año 2018 • Pág. 14
Ramón Ángel PONS Murguía 1; Eulalia María VILLA González del Pino 2; Rogelio CHOU Rodríguez 3
Recibido: 05/03/2018 • Aprobado: 19/04/2018
RESUMEN: El presente trabajo es el resultado de una investigación realizada para optimizar el consumo de energía en un proceso secado de madera, utilizando la estrategia de diseño experimental denominada Metodología de Superficies de Respuesta (RSM). Los parámetros significativos del proceso fueron identificados mediante el Análisis de Varianza (ANOVA). La determinación de los valores óptimos de estos parámetros, permitió obtener ahorros significativos y una disminución del reproceso mediante la reducción del índice de consumo de vapor. |
ABSTRACT: The present work is the result of a research carried out to optimize energy consumption in a drying wood process, using the experimental design strategy called Response Surface Methodology (RSM). The significant parameters of the process were identified through the Analysis of Variance (ANOVA). The determination of its optimal parameters values allowed the achievement of significant savings and a reduction of the rework by reducing the rate of steam consumption. |
La madera es un tejido vivo que comienza a degradarse desde la tala, por lo que es fundamental alcanzar un nuevo equilibrio con el medio para garantizar un producto útil y duradero. Desde este punto de vista, la calidad y la duración del producto, están en relación directa con el proceso de secado que ha sufrido la misma (Cruz de León, 2012; Ulloa, 2017).
Para llevar a cabo el proceso de secado, básicamente se calienta aire hasta temperaturas cercanas a los 190°C y se aprovecha el potencial térmico para evaporar y absorber la humedad presente en la madera. Para realizar dicho calentamiento, son varias las fuentes primarias y secundarias de energía utilizadas, pero las más frecuentes son el vapor sobrecalentado, el gas natural y las resistencias eléctricas (Chejne, 2015; Ulloa, 2017).
La optimización del consumo energético de este proceso no sólo disminuye el porcentaje de reproceso, sino que impacta directamente en la reducción del costo de producción, lo cual mejora la competitividad de las empresas en un mercado cada vez más exigente (Correa & Borroto, 2014).
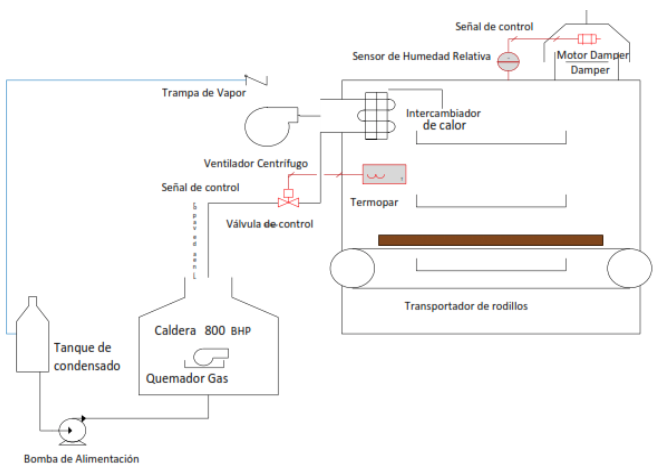
El sistema de secado utiliza vapor generado en una caldera de 800 BHP, que circula por un intercambiador de calor y mediante flujo cruzado, se calienta el aire hasta valores de temperatura entre 172 y 200°C. El aire entra en contacto directo con la madera que es alimentada por operarios y movida a través del secador mediante un transportador de rodillos.
El operador tiene la facultad de graduar dos niveles de temperatura, de acuerdo con el rango anteriormente mencionado, y modificar la velocidad de avance de la madera a través del equipo, de acuerdo con la experiencia y el porcentaje de resecado que habitualmente se encuentra entre el 50 y el 60%, es decir, más de la mitad de la madera que entra al proceso de secado, debe ser reprocesada.
El sistema tiene otra variable que es fundamental, la humedad. Cuando el aire internamente comienza a saturarse, un sensor de humedad relativa envía una señal de control a un dámper que se abre completamente y mediante el tiro natural del secadero, evacúa el aire que ya ha disminuido su temperatura y ha aumentado su humedad relativa. Estos valores de humedad usualmente son ajustados en dos niveles: 30 ó 40%. La Figura No. 1 muestra el esquema del proceso de secado.
De esta forma, el secado es un proceso cerrado de aire, con control sobre la velocidad de avance del material, la humedad relativa y la temperatura del aire presente en la cámara de secado.
La optimización del consumo energético de este proceso no sólo disminuiría el porcentaje de reproceso, sino que impactaría directamente en la reducción del costo de producción, lo cual mejoraría la competitividad de las empresas en un mercado cada vez más exigente. Para obtener las condiciones de operación que condujeran a obtener el valor óptimo del índice de consumo de vapor en el proceso, se empleó la Metodología de Superficies de Respuesta (RSM) con una estrategia experimental de Box – Behnken (Montgomery, 2013; Gutiérrez, 2013; Ulloa, 2017).
Son muchos los factores que preocupaban a los ingenieros de producción de esta planta:
Figura No.1
Esquema del proceso de secado
Teniendo en cuenta todo lo anterior, se llegó a la conclusión de que una forma de involucrar todos los aspectos que resultaban de interés para los ingenieros de planta, era considerar el índice de consumo de libras de vapor por metro cúbico de madera seca. De esta forma, al hacer mínimo el consumo de vapor, éste índice se reduciría; al minimizar el porcentaje de resecado la productividad aumentaría, y consecuentemente, el volumen de madera seca también lo haría, bajando nuevamente el indicador. En este caso, este indicador es una característica del tipo “El menor es mejor” (Correa & Borroto, 2014).
El análisis anterior condujo a la determinación de realizar una caracterización energética del secadero, con vistas a determinar los valores de sus parámetros de operación, para reducir los índices de consumo de vapor y el reproceso (Correa & Borroto, 2014; Lekshmi & Pillai, 2015; Quintero- Márquez, 2016).
Resulta interesante que este sistema fue objeto de una caracterización energética, cuya duración fue dos meses, que determinó que el índice de consumo crítico se encontraba alrededor de 2 446 Lb de vapor/m3 de madera seca, para valores altos del volumen de producción. Estos resultados se muestran en la figura 2.
Figura No.2
Diagrama del índice de consumo (IC) vs Producción (P)
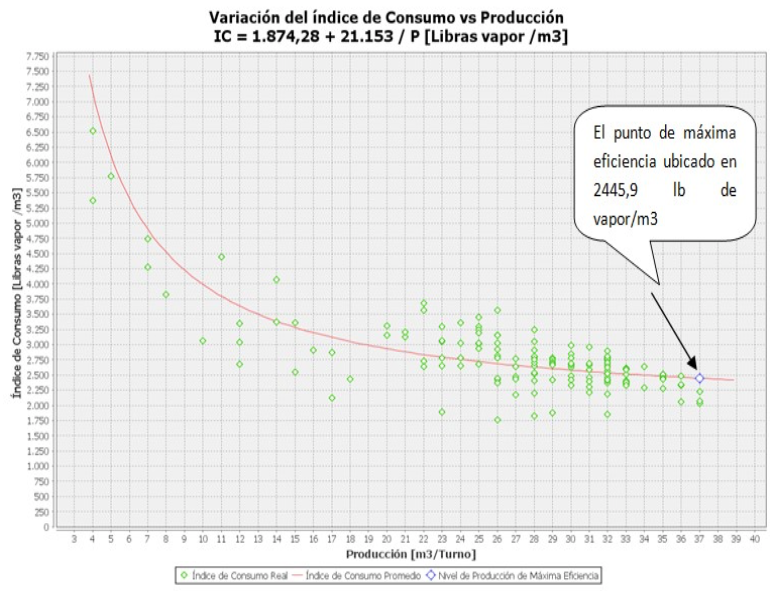
Esta caracterización reveló que el volumen de la producción crítica fue de 37 m3 de madera seca por turno, y que cuando se obtuvo ese nivel de producción, no hubo variaciones significativas en el índice de consumo, por lo que el proceso resultó ser más eficiente. Sin embargo, no fue posible determinar las condiciones de operación que condujeran a la obtención de este indicador de manera sistemática.
La pregunta fue entonces, ¿cómo lograr esos niveles de producción?, en este sentido, se llegó a la conclusión de que el diseño de experimentos podría ofrecer resultados muy importantes que soportaran la caracterización energética.
El diseño de experimentos (DOE) es una herramienta eficaz para maximizar la cantidad de información obtenida de un estudio, al tiempo que se minimiza la cantidad de datos recopilados (Montgomery, 2013; Pons & Villa, 2016).
En la investigación realizada, se empleó el diseño de experimentos para hallar cuál debía ser la combinación de los valores de las variables de control del proceso que condujeran al rendimiento óptimo del sistema. El experimento se diseñó con las siguientes variables:
Variables controladas:
Variables no controladas:
La corrida del experimento se realizó manteniendo fijo el tipo de madera (cativo) y variando las otras tres variables controladas. Se consideraron tres niveles, alto, medio y bajo, para cada variable, en correspondencia con los rangos de operación del proceso que fueron empleados para efectuar su caracterización energética. Estos niveles se muestran en la Tabla 1.
Tabla 1
Niveles de las variables de control
Variable de control |
Nivel bajo (-1) |
Nivel medio (0) |
Nivel alto (+1) |
Temperatura |
172 0C |
186 0C |
200 0C |
Humedad relativa |
30% |
35% |
40% |
Velocidad de avance |
10 m/s |
14 m/s |
18 m/s |
Los estudios realizados por Correa y Borroto (2014), recomiendan la exploración de modelos de segundo orden para definir la relación entre el índice de consumo energético y las variables de proceso que lo hacen variar de manera significativa. Tomando en consideración lo anterior, se decidió la exploración de una superficie de respuesta, haciendo variar las variables de control en los niveles establecidos.
La metodología de superficie de respuesta (RSM) es una colección de métodos estadísticos y matemáticos que son útiles para modelar y analizar problemas de ingeniería. Esta cuantifica la relación entre los variables de entrada y de proceso controlables con las variables de respuesta obtenidas (Gutiérrez, 2013; Pons & Villa, 2016).
El procedimiento de diseño de la metodología de superficie de respuesta es el siguiente (Montgomery, 2013):
I. Diseño de una serie de experimentos para la medición adecuada y confiable de la respuesta de interés.
II. Desarrollo de un modelo matemático de la superficie de respuesta, de segundo orden, con los mejores ajustes.
III. Determinación del conjunto óptimo de valores de las variables experimentales.
En la presente investigación, el objetivo fue determinar el conjunto de valores de las variables de control que permitiera optimizar el índice de consumo de vapor del proceso de secado. Se empleó un diseño Box-Behnken por ser éste eficiente para instalar polinomios de segundo orden en superficies de respuesta. Con menos puntos y menos costo que los diseños compuestos centrales y otras estrategias experimentales con el mismo número de factores, el diseño asegura que todos los parámetros del proceso operen en un nivel que no afecte la seguridad de las personas y las instalaciones.
Los experimentos se realizaron de acuerdo con una matriz de 15 corridas del diseño Box-Behnken, en orden aleatorio, para evitar un error estadístico en los análisis, debido a la acción de variables no controlables. La adecuación del modelo también se comprobó mediante el Análisis de Varianza (ANOVA). La optimización numérica de los parámetros de operación del proceso se realizó mediante el uso del software Statgraphics V. 17 (Polhemus, 2017).
Para estudiar los efectos de las variables controlables del proceso (X1: temperatura, X2: humedad relativa, X3: velocidad de secado) sobre la variable de respuesta Y (índice de consumo de vapor) fue ajustado el modelo codificado siguiente:
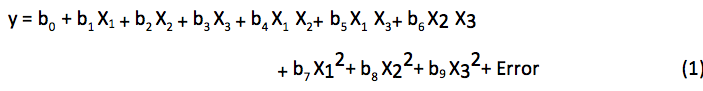
Los resultados de las corridas del experimento se muestran en la Tabla No. 2.
Tabla No. 2
Resultados de las corridas experimentales del diseño Box- Behnken
Corrida |
Temperatura (0C) |
Humedad relativa (%) |
Velocidad (m/min) |
Índice de consumo (lb vapor/m3) |
1 |
172,0 |
30,0 |
14,0 |
2642,5 |
2 |
200,0 |
30,0 |
14,0 |
2963,3 |
3 |
172,0 |
40,0 |
14,0 |
2552,6 |
4 |
200,0 |
40,0 |
14,0 |
2887,3 |
5 |
172,0 |
35,0 |
10,0 |
2630,6 |
6 |
200,0 |
35,0 |
10,0 |
2942,3 |
7 |
172,0 |
35,0 |
18,0 |
2569,5 |
8 |
200,0 |
35,0 |
18,0 |
2895,2 |
9 |
186,0 |
30,0 |
10,0 |
2829,7 |
10 |
186,0 |
40,0 |
10,0 |
2622,3 |
11 |
186,0 |
30,0 |
18,0 |
2505,9 |
12 |
186,0 |
40,0 |
18,0 |
2595,7 |
13 |
186,0 |
35,0 |
14,0 |
2519,2 |
14 |
186,0 |
35,0 |
14,0 |
2525,9 |
15 |
186,0 |
35,0 |
14,0 |
2541,5 |
El análisis de varianza que se muestra en la Tabla 3 y el diagrama Pareto de efectos estandarizados de la Figura 3, indican que el efecto principal de primer orden de la variable humedad relativa y algunas interacciones de segundo orden de las variables controlables, no ejercen una influencia significativa sobre el comportamiento del índice de consumo.
Sin embargo, resultó contradictorio que el efecto principal de primer orden de la variable humedad no fuera significativo, aunque el p-valor es cercano al nivel de significación, porque al aumentar la humedad relativa se debía esperar un aumento del índice de consumo de vapor para lograr el secado de la madera. En la teoría y la práctica del diseño de experimentos, cuando se presentan estas situaciones, entre otras alternativas, se recomienda eliminar aquellos efectos que no sean significativos para aumentar los grados de libertad de la varianza del error (Montgomery, 2013; Gutiérrez, 2013).
Tabla 3
Análisis de Varianza para Índice de consumo
Fuente |
Suma de Cuadrados |
Gl |
Cuadrados Medios |
Razón-F |
Valor-P |
A: Temperatura |
208949, |
1 |
208949, |
131,80 |
0,0001 |
B: Humedad relativa |
10046,5 |
1 |
10046,5 |
6,34 |
0,0533 |
C: Velocidad |
26289,2 |
1 |
26289,2 |
16,58 |
0,0096 |
AA |
115388, |
1 |
115388, |
72,78 |
0,0004 |
AB |
48,3025 |
1 |
48,3025 |
0,03 |
0,8683 |
AC |
49,0 |
1 |
49,0 |
0,03 |
0,8673 |
BB |
11487,9 |
1 |
11487,9 |
7,25 |
0,0432 |
BC |
22082,0 |
1 |
22082,0 |
13,93 |
0,0135 |
CC |
10669,0 |
1 |
10669,0 |
6,73 |
0,0486 |
Error total |
7927,01 |
5 |
1585,4 |
|
|
Total (corr.) |
402538, |
14 |
|
|
|
-----
Figura No.3
Diagrama de Pareto de los efectos de las variables de control
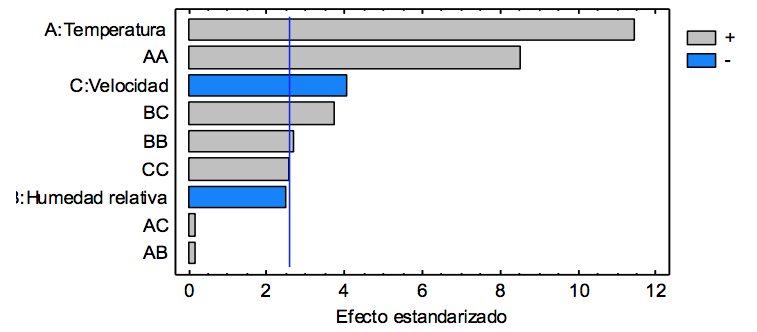
Esto condujo al mejor análisis de varianza denominado BEST ANOVA. La Tabla 4 muestra el mejor análisis de varianza (BEST ANOVA) de las corridas experimentales. Se observa que los efectos principales lineales, incluido el de la humedad relativa, así como los efectos principales cuadráticos de las variables controlables son significativos, esto es, afectan de manera significativa el comportamiento del índice de consumo del proceso. El diagrama de Pareto de la Figura 4 confirma los resultados del análisis de varianza.
El modelo cuadrático no presentó falta de ajuste, por tanto, es adecuado para predecir futuros valores del índice de consumo. El valor del estadístico R cuadrado ajustado indica que el 96,031 % de la variabilidad total fue explicado por el modelo de regresión cuadrático.
Tabla 4
Análisis de Varianza para Índice de consumo
Fuente |
Suma de Cuadrados |
G. L. |
Cuadrado Medio |
Razón-F |
Valor-P |
A: Temperatura |
208949, |
1 |
208949, |
182,28 |
0,0000 |
B: Humedad relativa |
10046,5 |
1 |
10046,5 |
8,76 |
0,0211 |
C: Velocidad |
26289,2 |
1 |
26289,2 |
22,93 |
0,0020 |
AA |
115388, |
1 |
115388, |
100,66 |
0,0000 |
BB |
11487,9 |
1 |
11487,9 |
10,02 |
0,0158 |
BC |
22082,0 |
1 |
22082,0 |
19,26 |
0,0032 |
CC |
10669,0 |
1 |
10669,0 |
9,31 |
0,0186 |
Error total |
8024,32 |
7 |
1146,33 |
|
|
Total (corregido) |
402538, |
14 |
|
||
R-cuadrada = 98,0066 % |
R-cuadrada (ajustada por g. l.) = 96,0131 % |
||||
-----
Figura No.4
Diagrama de Pareto de los efectos de las variables de control
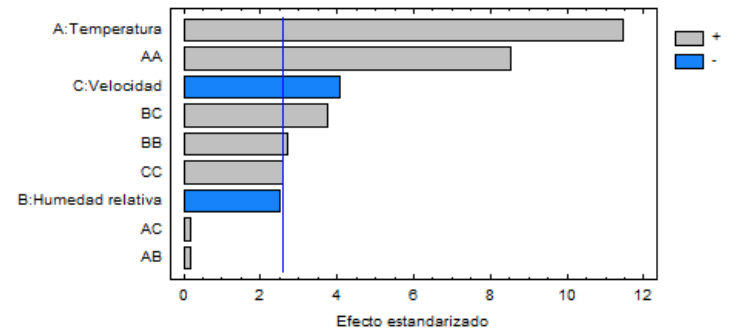
Los valores estimados de los coeficientes de regresión del modelo de segundo orden, se muestran en la tabla 5.
Tabla 5
Coeficientes de regresión para Índice de consumo
Coeficiente |
Estimado |
constante |
37245,8 |
A: Temperatura |
-323,976 |
B: Humedad relativa |
-215,279 |
C: Velocidad |
-238,426 |
AA |
0,901935 |
BB |
2,23117 |
BC |
3,715 |
CC |
3,35964 |
El modelo de regresión de segundo orden ajustado, con las variables originales, fue el siguiente:
Índice de consumo = 37245,8 - 323,976*Temperatura - 215,279*Humedad relativa - 238,426*Velocidad + 0,901935*Temperatura2 + 2,23117*Humedad relativa2+ 3,715*Humedad relativa*Velocidad + 3,35964*Velocidad2 (2)
Este modelo fue utilizado para estimar los valores esperados del índice de consumo y la combinación de valores de las variables controlables para optimizar el proceso de secado.
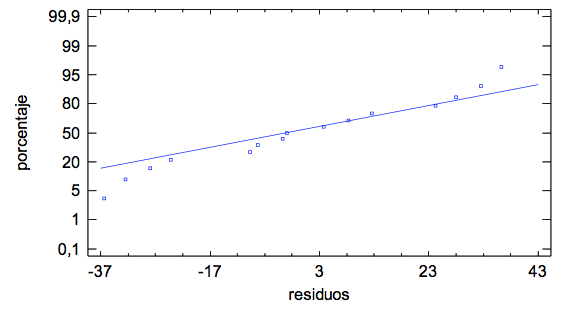
El propósito de esta etapa fue comprobar el cumplimiento de los supuestos de normalidad, estabilidad de la varianza e independencia. Los gráficos de residuos que se muestran en las Figuras 5, 6 y 7, respectivamente, expresan que no se aprecian violaciones de estos supuestos.
Figura No.5
Gráfico de probabilidad normal para residuos
-----
Figura No.6
Gráfico de residuos versus predichos para índice de consumo
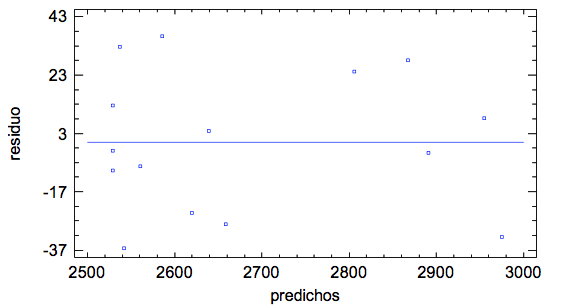
-----
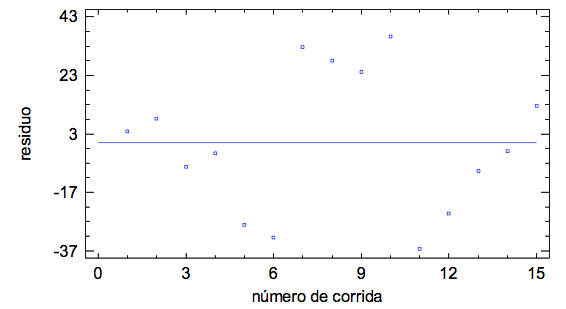
Figura No.7
Gráfico de residuos por número de corrida
El objetivo fue determinar la combinación de valores de la temperatura, humedad relativa en el dámper y velocidad de avance que hicieran mínimo el valor del índice de consumo de vapor en el proceso de secado de madera cativo. Los resultados obtenidos de la corrida del software fueron los siguientes:
Meta: minimizar Índice de consumo de vapor
Valor óptimo = 2476,5 lb de vapor/m3 de madera
Tabla 6
Valores que optimizan el índice de consumo de vapor
Factor |
Bajo |
Alto |
Óptimo |
Temperatura |
172,0 |
200,0 |
179,603 |
Humedad relativa |
30,0 |
40,0 |
34,6518 |
Velocidad |
10,0 |
18,0 |
16,3254 |
Figura No.8
Contornos de la Superficie de Respuesta Estimada
A partir de estos resultados el proceso comenzó a operarse con los siguientes valores:
Temperatura: 179, 6 ºC
Humedad relativa a la entrada del dámper: 34,7 %
Velocidad de avance: 16, 3 m/min.
Se llevaron a cabo experimentos de confirmación para validar si los valores obtenidos del índice de consumo, bajo condiciones normales de operación del proceso, no mostraran grandes desviaciones respecto al valor óptimo que fue determinado bajo condiciones experimentales. Un conjunto de 12 experimentos de confirmación llevados a cabo con la configuración óptima produjo resultados que presentaron desviaciones menores que 20 lb de vapor/m3 de madera procesada, en relación con el valor óptimo. También se logró una reducción promedio del reproceso equivalente al 25%, en relación con los valores obtenidos antes de la experimentación.
Por lo tanto, la configuración estimada se consideró óptima para procesar volúmenes de madera con una mejor eficiencia energética y un índice de reproceso más bajo.
En esta investigación, la optimización paramétrica para hacer mínimo el índice de consumo de vapor en el proceso de secado de madera cativo, se realizó mediante la aplicación de la Metodología de Superficies de Respuesta utilizando un diseño de experimentos de Box-Behnken. Las principales variables del proceso identificadas como responsables de la variación del índice de consumo fueron la temperatura interna en la cámara de secado, la humedad relativa de accionamiento del dámper de extracción de aire saturado y la velocidad de avance del material a través del secadero. Cada factor se analizó con tres niveles diferentes según la matriz del diseño Box - Behnken. Se estudió la contribución de estos factores usando pruebas ANOVA para estimar sus efectos principales y de interacción. Las pruebas ANOVA revelaron que los efectos principales lineales y cuadráticos de estas variables de proceso fueron altamente significativos en la reducción del índice de consumo de vapor del proceso de secado de la madera.
A partir de los resultados de las pruebas estadísticas anteriores se ajustó un modelo de regresión de segundo orden, con el cual se obtuvo la configuración paramétrica óptima de los variables del proceso. La configuración determinada mediante el empleo del Software Statgraphics Centurión fue la siguiente:
Temperatura: 179, 6 ºC
Humedad relativa a la entrada del dámper: 34,7 %
Velocidad de avance: 16, 3 m/min.
Los experimentos de confirmación realizados permitieron validar los resultados obtenidos durante la investigación experimental, lográndose una reducción promedio del reproceso equivalente al 25%, en relación con los valores obtenidos antes de la experimentación. Por tanto, esta investigación confirmó cuán útil es el diseño de experimentos en la mejora del desempeño de los procesos, pues con un número limitado de corridas se pudo determinar la manera óptima de operar el proceso, lo cual no fue posible mediante una caracterización energética que exigió tiempo y muchos recursos. Los valores del índice de consumo de vapor determinado con ambos métodos, mostraron en promedio diferencias no mayores de 20 lb de vapor/m3 de madera tratada.
Chejne, F. (2015). Recuperación de energía en procesos industriales. Medellín: Universidad Nacional de Colombia.
Correa, J., y Borroto, A. (2014). Diseño y aplicación de un procedimiento para la planificación energética según la NC ISO 50 001: 2011. Ingeniería Energética, 35 (1), 38-47.
Cruz de León, J. (2012). Secado de Madera Aserrada: Ciencia y Tecnología. Madrid: Editorial Academia Española.
Gutiérrez, H. (2013). Análisis y Diseño de Experimentos. México: Mc Graw – Hill.
Lekshmi, K., y Pillai, V. (2015). Boiler Blowdown Analysis in an Industrial Boiler. IOSR. Journal of Engineering (IOSRJEN), 5 (7), 22-28.
Montgomery, D. (2013). Design and Analysis of Experiments. New York: John Wiley& Sons.
Polhemus, N. (2017). Statgraphics Centurion 17 User Guide. The Plains, Virginia: Stat point Technologies Inc.
Pons, R., Villa, E., Bermúdez, Y., y Hernández, J. (2016). Quality Improvement of a Casting Process using Design of Experiments. Prospectiva, 14 (1), 42-53.
Quintero -Márquez, A., Bernard, C., Zoulaliam, A., y Regaurme, Y. (2016). Balance de energía en un horno de secar madera. Revista Tecnología Química (Cuba), 36 (1), 20-25.
Ulloa, J. (2017). Gestión Energética del Secado Industrial de Madera. Madrid: Editorial Academia Española.
1. Doctor en Ciencias Técnicas. Docente Investigador, Facultad de Ingeniería Industrial. Universidad de Guayaquil, Ecuador. rpons2015@gmail.com
2. Doctor en Ciencias Técnicas. Docente Investigador, Facultad de Ingeniería Industrial . Universidad de Guayaquil, Ecuador. eulaliamariavilla7258@gmail.com
3. Doctor en Ciencias Técnicas. Docente Investigador, Facultad de Gestión Empresarial . Universidad Metropolitana, Ecuador. rogchou@yahoo.com