ISSN 0798 1015

Vol. 38 (Nº 49) Year 2017. Page 18

Analysis of risk assessment methods of innovative projects

Análisis de los métodos de evaluación de riesgos de proyectos innovadores

Elena Vladimirovna TARASOVA 1; Elena Nikolaevna NIKULINA 2; Natalia Valerievna MOSKVICHEVA 3

Received: 12/06/2017 • Approved: 20/07/2017

Content

1. Introduction

2. Risk analysis methods

3. The proposed method

4. Results and discussion

5. Conclusion

References

1. Introduction

The implementation of innovative projects at developing enterprises of high tech industries is related to the high level of risk. Increasing agility of economic processes, rapid changes in external business conditions, capital mobility, as well as high rates of technological progress lead to higher uncertainty and impede reliable assessment of the efficiency of investment funds. Management of innovative projects implementation aimed at the development of new products and new activities requires the use of scientifically grounded tools and methods, ensuring maximum consideration of current risks for making optimal decisions (Nikulina and Tarasova 2014).

Risk is an objective phenomenon related to the uncertainty of occurrence of non-desirable event. In turn, uncertainty is the incompleteness and inaccuracy of information about project implementation conditions, future costs and expected results, caused by lack of knowledge about the economic environment. Innovation activity is always associated with risks (Troshin, Burdina and Razzhevaikin 2012; Horn and Wachowicz, 2015). This is due to the fact that innovations make significant and sometimes radical changes into production processes that complicate the basic functions of management, namely analysis and decision making (Risk management of innovation project, 2009). A variety of innovations’ implementation methods in the context of dynamically developing market environment steps up the risk of an unsuccessful result due to not only errors, but also due to random coincidence.

There are various manifestations of risk situations (Gracheva, and Lyapina, 2010):

• The result has not been achieved;
• The result is below expectations: technical or economic characteristics of the innovation appeared to be worse than those expected by the enterprise management;
• The result has been achieved later: the purpose of innovation activity has been reached, though it happened later than expected;
• The result is more expensive than expected: an innovative project was implemented, though over-spending exceeded initial estimates.

The main criteria of investment efficiency into innovative project include profitability, risk, and horizon period. The interrelation of "risk-profitability" is a motivating factor of decision making under uncertainty conditions. High-risk projects are selected for implementation only at the expectation of significant returns.

Innovative project risk management is a totality of processes associated with identification, risk analysis, and decision making that includes maximization of the positive and minimization of the negative consequences of occurrence of risk events. One of the fundamental stages in innovation project risk management is exactly the analysis of the innovation activity risks. The results of the project, innovation and competitiveness of the enterprise in general are largely dependent on the quality of risk analysis (Moskvicheva, Burko and Sokolova, 2014).

There are many different risk classifications in the finance theory. However the most common approach in the investment analysis is their division into systematic risks and nonsystematic risks (Nikulina and Tarasova 2006).

Systematic risks are determined by the market environment of the operating business. They are also often referred to as external risks or environment-related risks. Among them we can distinguish the common systematic risks and branch risks. The first risks will determine the activities of all companies operating in the country, regardless of their industry sector. Such risks include in particular, inflation, changes in currency exchange rates, political climate, etc. (Burdina, and Solovieva, 2013). The second risk category depends on the sectoral affiliation of the company and is influenced by the factors such as the nature of competition among resources’ suppliers, customers' needs, and specificity of used assets (for example, special equipment). Nonsystematic risks are internal factors influencing a particular business faced by the concerned enterprise (Troshin, Burdin, Moskvicheva, Tarasova, and Nikulina 2016).

Main groups of nonsystematic risks as well as measures to minimize them are presented in Table 1 (Spiridonova, 2016). 

Table 1
Main groups of nonsystematic risks of the innovation
project and some ways of their minimization

A list of nonsystematic risks for innovation projects represented in Table 1 is not complete. There are also risks in management, in project implementation in terms of schedule deadlines and milestones, corporate risks of a private nature, peculiarities of small businesses operation, and some other risks (Moskvicheva, Troshin, and Fomkina, 2013; Troshin, Burdin, Moskvicheva, Tarasova, and Nikulina, 2016).

Industry-specific systematic and nonsystematic risks are accounted for in cash flows of the innovation project, the overall systematic risks are accounted for in the discount rate.

2. Risk analysis methods

The following groups of methods can be distinguished for quantitative risk analysis applied in the investment design: methods to adjust cash inflows and the discount rate; sensitivity analysis method of investments efficiency criteria; and probabilistic and statistical methods (Nikolaev, 2006).

The choice of specific method of investment risk analysis depends on the capabilities of the information base, requirements to the final results (indicators) and the security level of investment management (Nikulina and Tarasova 2014).

The main variety of the risk adjusted discount rate approach (RADR) is the calculation of discount rate as weighted average cost of capital adjusted for risk ( ). Methods of determining adjustments for the risk differ depending on information framework of the analysis and the adopted investment policy of the enterprises. The magnitude of the risk premium is determined by environment-related risks of the project (Moskvicheva, Nikulina, Tarasova, and Fomkina, 2011; Troshin, Burdin, Moskvicheva, Tarasova, and Nikulina 2016).

Certainty equivalent method involves the adjustment of cash flows of the investment depending on the reliability of estimates of their expected value. This is done by multiplying project net income at the time point  by reduction factor. The magnitude of the correction factor depends on the level of operational, technological, and market risks.

A common drawback of all integrated calculation methods of efficiency indicators adjusted for risk is an implicit accounting for the degree of risk sensitiveness to investors. The methods are based on the use of average market values.

The sensitivity analysis method of investment efficiency criteria (the what-if analysis tools) allows for a quantitative assessment of the impact on the project of its key variables change. The method consists in the elimination of influence of each factor of the cash flow model and net present value (or other criterion) and the evaluation of the response of the resultant indicator (net present value, NPV; internal rate of return, IRR, and discounted pay-back period, DPP) to changes in key variables (volume of sales, prices on products and production resources, and cost of capital). At that, the limiting values of these variables at which the project still remains effective are determined (Nikulina and Tarasova 2014).

Available safety margin is compared with subjective or statistical estimate of key variables variation. The method can be modified taking into account correlations between key variables. The ratio of the change in the effective index to change in key variable is called the sensitivity coefficient, which is calculated in the same way as elasticity. The advantage of sensitivity analysis is the identification of variables that are most important for the success of the investment project. It is used to study the influence of changing specific basic variables on the investment efficiency, provided that the other variables remain unchanged (Nikulina, Tarasova, Troshin, and Fomkina, 2009). However, the principles and mechanisms of its application do not allow calculating the probability of changes as well as probabilistic indicators of the formation of exactly given NPV rather than the other. Therefore, this method may serve only the source of information for more accurate methods to account the risk. The sensitivity analysis of investments efficiency criteria gives the opportunity to assess the impact on the project of changes in its key variables as well as safety margin of these factors, though does not contain tools to calculate the risk magnitude.

Scenario method involves the forecasting of development options of the external environment and the estimates of investment efficiency for each scenario (Nikulina and Tarasova 2006). Assigning certain probabilities to scenarios, we can construct a risk profile, as well as assess the standard deviation, and the skewness of distribution. The so-called "worst-case scenario", "most likely scenario", and "optimistic scenario" are often used to assess the project that allows evaluating approximately the scatter of the project results and its profitability (or loss-making) in case of deterioration of the economic situation. Scenario method involves the following technique:

• Defining several change options of key base indicators (e.g., the worst-case, the most likely, and optimistic scenario).
• Assigning certain probabilistic assessment to each change option.
• Calculating the probable values of NPV (or IRR, or PI) as well as estimating deviations from the mean for each option.
• Carrying out the probability distributions analysis of the results obtained.

The project with the smallest value of standard deviation and variation coefficient is considered less risky.

In general, the method allows obtaining a very clear picture for different options of projects implementation as well as provides information about sensitivity and possible deviations.

A method of constructing "decision tree" is similar to the scenarios method and is based on the construction of multiple-choice prediction of the external environment dynamics. Unlike the scenarios method, this technique suggests enterprise the possibility of making own decisions that change the course of the project implementation (making choice) and a special graphical presentation of results ("decision tree"). "Decision tree" can be used both under risk and under uncertainty or full certainty. The analyst calculates the selected efficiency criterion (e.g., NPV) along each "branch" of the tree, while in case of risk analysis he assesses also the probability of each value. The obtained values can be used to construct probability curve and choose the optimal option for project implementation. In the general case, the use of this method involves implementing the following steps (Nikulina and Tarasova 2006).

• Defining the problem and all possible options of the further events for each point of time .
• Laying on the tree the node corresponding to the problem, and the arcs coming out of the node.
• Assigning each outgoing arc with its monetary and probabilistic assessment.
• Calculating probable value of NPV (or IRR or PI) based on values of all nodes and arcs.
• Carrying out probability analysis of distributions of the results obtained.

The advantage of "decision tree" is the clearness of results and process analysis, while the disadvantage is its technical complexity at large sizes of “tree”.

Simulation modeling of investment processes is the most powerful and sophisticated tool for investment risk analysis and requires the use of appropriate software. Stochastic simulation is known under the name of "Monte Carlo method". The simulation modeling technique consists of several stages: identifying the deterministic and stochastic dependencies of internal variables of the project and variables of external environment, building the model, carrying out simulation based on random variations of key variables, plotting probability curves, and calculating risk factors based on the simulation results (Nikulina and Tarasova 2006).

In the general case, conducting a simulation experiment can be divided into the following stages.

• Establishing the relationships between the source and output indicators in the form of mathematical equation or inequality.
• Specifying the probability distribution for the key parameters of the model.
• Conducting computer simulation of the key parameters of the model.
• Calculating the main distribution characteristics of the source and output indicators.
• Carrying out analysis of obtained results and making a decision. The results of simulation experiment can be complemented by statistical analysis as well as used to build predictive scenario models.

The accuracy of the estimates largely depends on the quality of initial assumptions and accountancy of relationships of the variables in the external environment. Contemporary software tools allow taking into account the shape of the probability curve and correlation of dozens of external variables, however, estimating these values in practical examination is usually impossible. Investment analysts measure the variations of key variables of the macro- and microenvironment, assessing the spread in magnitudes of the secondary variables and statistical relationships between factors by expertise. Therefore, the capabilities of simulation models usually are not fully utilized.

The risk analysis algorithm when using probability and statistical methods can be described as follows:

• Determining key factors of the investment project. To do this, it is suggested to use sensitivity analysis with regard to all factors (cost of R&D, selling price, advertising budget, sales volume, product cost, etc.) using application-specific software packages such as Project Expert and Alt-Invest that will allow reducing computation time significantly. Factors, whose change lead to the largest deviations of the net present value (NPV), are selected as key factors.
• Defining the maximum and minimum values of key factors, and setting the probability distribution. In general case, use of a normal probability distribution is recommended.
• Carrying out simulation of key factors based on the selected distribution; the obtained values are used to calculate NPV.
• Calculating criteria that quantitatively characterize the risk of the investment project (mathematical expectation of NPV, dispersion, root-mean-square deviation, and variation coefficient) based on the data resulting from simulation.

Practical application of probabilistic and statistical methods for risk assessment of innovation projects is quite difficult due to lack of statistics, while simulation data may not give quite accurate information, because are based on judgment-based definition of probability and distributions laws. Calculation methods of statistical probabilities suggest the availability of a given degree of homogeneity within the selected class of risk events, while innovative solutions relate to such unique situations that cannot be subjected to statistical grouping. In this regard, the assessment of innovative risks is not based on statistical analysis, but rather intuitive. This makes it necessary to take into account qualitative risk assessments when carrying out quantitative analysis.

3. The proposed method

Scenario and probabilistic risk analysis methods are gradually becoming outdated. They are replaced by fuzzy multiple-criteria approach, which, on the one hand, is free from axiomatic probability as well as the problem concerning selection of probability weights, and on the other hand, include all the possible scenarios of events. A fuzzy multiple-criteria approach allows taking into account in the financial model of the economic entity qualitative aspects that do not have exact numerical evaluation. This approach makes it possible to combine, while estimating, the account of quantitative and qualitative attributes that dramatically increases the level of adequacy of the applied methods.

The uncertainty of the investment project environment is a fatal quality of the market, due to the fact that market conditions are dependent on large number of simultaneously applying factors of different nature and orientation, which are not subjected to aggregate valuations. The economy continuously generates changing economic conditions that is stipulated by the dynamics of macroeconomic factors and the rapid pace of technological progress. As far as the uncertainty is increasing, classical probabilistic descriptions give way, on the one hand, to subjective probabilities, based on expert estimation, and, on the other hand, to the probabilities, which are defined qualitatively rather than quantitatively. At that, point estimates of probability distributions are replaced by interval estimates (for expert methods) and triangular-fuzzy estimates (for methods of the fuzzy sets theory). In the risk analysis of investment project based on fuzzy-multiple approach, the concept of randomness is replaced by the concepts of expectancy and opportunity.

In the framework of innovative projects’ risk assessment it is appropriate to use triangular fuzzy numbers with membership function of the following form: "the net present value of the project is approximately equal to the expected value and definitely is within the range between the worst-case scenario and optimistic scenario " (Fig. 1).

Fig. 1
Triangular fuzzy number (NPVmin, NPVav, NPVmax)

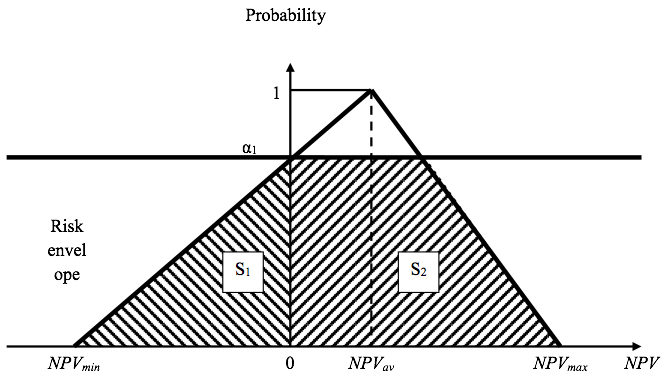
When considering the meaning of the RE parameter, we can take it for an "instability factor" of the investment project, which shows how significantly is biased the expected value of NPV towards the minimum value. From a mathematical point of view, the RE parameter is the ratio between the areas of the figure (S1) located in the negative region, and the figure (S2) situated in the positive quarter of the coordinate system (Fig. 1).

The higher the value of RE, the greater the risk of an innovation project.

Fuzzy multiple-criteria approach overcomes the shortcomings of probabilistic and mini-max approaches associated with taking into account the uncertainty. First, here a full range of possible scenarios of the investment process is formed. Second, the decision is made based on the entire set of estimates rather than just two estimates of the project efficiency. Third, the expected effectiveness of the project is not a point indicator, but represents a field of interval values with its distribution of expectations, characterized by the membership function of the corresponding fuzzy number. At the same time, balanced complete set of expectations allows estimating an integrated measure of expectation of negative results of the investment process, i.e. the degree of investment risk (Nikolaev 2006).

Thus, the method based on the fuzzy sets theory allows determining the risk of inefficiency of the investment project based on three development scenarios: the worst-case scenario, the most likely scenario, and optimistic scenario.

In this case, the calculation will be represented by the following sequence of actions.

1. Planning of three cash flows for each period t: optimistic (in which there are no risk factors), the worst-case scenario (scenario, in which there are all risk factors), and the most probable scenario (is determined on the basis of expert estimation).
2. Calculating the NPV indicator for each cash flow option of the project at all three possible scenarios. At that, the optimistic cash flow is discounted at a risk free rate equal to government bond yields comparable in terms of currency and period; the most likely cash flow is discounted at a rate corresponding to the cost of corporate capital; while when calculating the worse-case value of the NPV, used discount rate should take into account all threats of the financial market.
3. Calculating the risk indicator RE.

Planning three options of cash flows is carried out when analyzing any investment project in the framework of the "scenario analysis" technique. Government agencies, such as for example, Federal State Budgetary Institution "Fund of assistance to development of small forms of enterprises in scientific-technical sphere", when taking the decision on granting of direct funding for an innovative project or development of a specific business, requires the availability of calculations based on optimistic, medium, and the worse-case scenarios presented in business plan.

However, the economic-statistical method of scenario analysis contains a number of shortcomings. In particular, each scenario is assigned a probability of its occurrence solely on the basis of expert estimation (and hence with a high degree of subjectivity). Therefore, the evaluation results can be strongly distorted. Besides, the use of a simplified modification of the scenarios method is possible only under condition of normal distribution of probabilities. Otherwise, it is necessary to apply more detailed calculation, predicting the aggregate of scenarios (certain analogue of a tree of objectives) and analyzing the probability of each of them. The considered method of calculating the project risk factor based on the theory of fuzzy sets is devoid of the indicated shortcomings.

4. Results and discussion

As an example let’s consider eight innovative projects. For each project there are NPV indicators calculated for the worse-case (NPVmin), the most probable (NPVav), and optimistic (NPVmax) scenarios. Besides, risk factors such as the range of variation VAR, variance D, the standard deviation σ, variation coefficient CV, and RE are determined for each project. The results of the calculation of VAR and RE indicators are presented in Table 2.

Table 2
Calculation of VAR and RE risk factors

To calculate the statistical variability indices (E(NPV), D, σ, СV) we consider suggested by the experts four distribution laws of random discrete value NPV, presented in Table 3.

------

Table 3
Distribution laws of NPV indicator

Calculation of statistical indicators according to the given distribution laws is presented in Tables 4 – 7.

------

Table 4
Statistical indicators calculated according to the law P1

-----

Table 5
Statistical indicators calculated according to the law P2

-----

Table 6
Statistical indicators calculated according to the law Р3

------

Table 7
Statistical indicators calculated according to the law Р4

The performed calculations allowed drawing the following conclusions:

Based on assessment of the VAR variation range, project No. 8 is the most risky. However, the risk factor RE in this project is minimal, because the triangle fuzzy number is maximally shifted towards positive values of project return. The triangular fuzzy number of this project is shown in Fig. 2. The ratio of the triangle area (S1), which is in the negative plane, to the triangle area (S2), which is in the positive plane, is minimal.

Fig. 2
Triangular fuzzy number of the project No. 8.

The most risky is the project No 6. The risk factor RE of this project is maximal. As can be seen in Fig. 3, the major part of the triangular number is located in a negative region.

Fig. 3
Triangular fuzzy number of the project No. 6.

Independently of the NPV distribution law, proposed by the experts, all risk indicators (σ, CV) have shown that project No. 6 is the most risky.

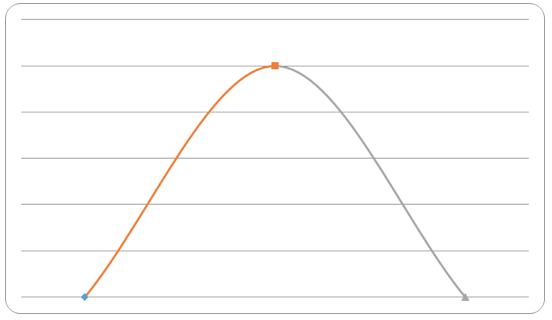
Calculations carried out with regard to the projects No. 3 and No. 8 are of special interest. Probabilistic and statistical methods (σ, CV) show that the level of risk of these projects is approximately the same. However, the RE indicator suggests that the probability of losses when implementing project No. 3 is higher. Triangular fuzzy number of the project No.3 is shown in Fig. 4. According to the risk profile, the ratio between negative and positive outcomes is higher than that for the project No. 8.

Fig. 4
Triangular fuzzy number of the project No. 3

• Statistical risk indicators, including volatility (σ) and variation coefficient (CV), characterize the scatter of the actual values of the rate of return of the project around the mathematical expectation of this random variable. At that, it is unimportant, whether actual rates of return are negative or positive. The use of these risk indicators is justified in the analysis of low-risky investment projects, which are mainly associated with the expansion or modernization of existing business. Implementing innovative projects is always associated with high probability of loss. Therefore, the use of fuzzy-multiple approach and the calculation of RE indicator allow obtaining more reliable result.

5. Conclusion

In order to develop effective methods of risk management of investment project, it is advisable to distinguish admissible, critical, and catastrophic levels of risk. Admissible risk is the risk not creating threats to the project implementation and not having a significant negative impact on key parameters of the project. Critical risk is regarded as a risk that may have a significant impact on key project parameters, though not creating the threats to project fulfillment. Catastrophic is the risk threatening the implementation of the project and capable of destabilizing the financial condition of the enterprise. Each risk level is characterized by a certain value of RE indicator. Barrier values of the risk indicator RE are determined based on processing of statistical data on the implementation of innovative projects at the enterprise in retrospective periods of time (Nikolaev 2006).

References

Brealy, R.A. and Myers, S.C., 1995. Fundamentals of corporate finance. N.Y., McGRAW-HILL INC.

Burdina, A.A. and Solovieva, I.V. 2013. Analiz metodov analiza finansovyh riskov predpriyatij aviacionnoj otrasli [Evaluation of analysis methods of financial risks of the aviation industry enterprises]. Economics and Entrepreneurship, 12-1(41-1), 659-663.

Gracheva, M.V. and Lyapina, S.Yu., 2010. Upravlenie riskami v innovacionnoj deyatel'nosti [Innovation risk management]. Tutorial, Moscow, YUNITI, 350 p.

Horn J.K. and Wachowicz, G.M., 2015. Osnovy finansovogo menedzhmenta [Fundamentals of financial management]. Textbook, Moscow: Williams Publishing House.

Moskvicheva, N.V. and Melik-Aslanova, N.O., 2015. Analiz osobennostej modernizacii proizvodstvennyh moshchnostej predpriyatij aviacionnoj promyshlennosti [Analysis of the modernization characteristics of production capacities of the aviation industry enterprises]. Bulletin of the Moscow Aviation Institute, 22(4), 208-213.

Moskvicheva, N.V., Burko, M.L., Sokolova, A.A., 2014. Ocenka investicionnoj privlekatel'nosti innovacionnyh programm predpriyatij aviacionnoj promyshlennosti [Evaluation of investment attractiveness of innovative programs of the aviation industry enterprises]. Proceedings of the 15th International scientific-practical conference, St.Petersburg, pp. 102-109.

Moskvicheva, N.V., Nikulina, E.N., Tarasova, E.V., and Fomkina, V.I., 2011. Voprosy ocenki stoimosti predpriyatij aviacionnoj promyshlennosti [The issues of the aviation industry enterprises valuation]. Monograph, Moscow, MAI-PRINT, 204 p.

Moskvicheva, N.V., Troshin, A.N., and Fomkina, V.I., 2013. Voprosy ehkonomicheskogo obosnovaniya processov reorganizacii predpriyatij aviacionnoj promyshlennosti [Issues of an economic substantiation of the processes of enterprise reorganization in the aviation industry]. Monograph, Moscow: MAI Print.

Nedosekin, A.O., 2003. Metodologicheskie osnovy modelirovaniya finansovoj deyatel'nosti s ispol'zovaniem nechetko-mnozhestvennyh opisanij [The methodological basis of financial activity simulation with the use of fuzzy multiple-criteria approach]. Higher Doctorate thesis in economics. St. Petersburg University of Economics and Finance, St.Petersburg, 280 p.

Nikolaev, Yu.V., 2006. Razrabotka modeli upravleniya riskami investicionnyh proektov na transportno-ehkspeditorskom predpriyatii [Development of risk management model of investment projects at the freight forwarding enterprise]. Ph.D. thesis in economics. Moscow Aviation University, Moscow, 253 p.

Nikulina, E.N. and Tarasova, E.V., 2006. EHkonomicheskaya ocenka investicij [Economic assessment of investments]. Tutorial. Moscow: MAI Print, 98 p.

Nikulina, E.N. and Tarasova, E.V., 2014. Analiz metodicheskogo obespecheniya tekhniko-ehkonomicheskogo obosnovaniya investicionnyh proektov v aviacionnoj promyshlennosti [Analysis of the methodological support of feasibility study of investment projects in the aviation industry]. Proceedings of the 15th International scientific-practical conference, St.Petersburg, pp. 148-155.

Nikulina, E.N. and Tarasova, E.V., 2014. Tekhnologiya kommercheskoj i innovacionnoj ocenki investicionnyh proektov v aviacionnoj otrasli [Commercial and innovative evaluation technology of investment projects in the aviation sector]. Bulletin of Rybinsk State Aviation Technical University named after P.A.Soloviov, 1(28), 151-157

Nikulina, E.N. and Tarasova, E.V., 2016. Metodika ocenki ehffektivnosti modernizacii ispytatel'nyh podrazdelenij predpriyatij po proizvodstvu letatel'nyh apparatov [Assessment technique of modernization efficiency of the testing divisions of the aircraft manufacturing enterprises]. Bulletin of Moscow State Technological University “Stankin“ (MSTU Stankin), 1(36), 91-95.

Nikulina, E.N., Tarasova, E.V., Troshin, A.N., and Fomkina, V.I., 2009. Finansovaya matematika dlya investora [Financial mathematics for investor]. Monograph. Moscow: MAI-Print, 184 p.

Spiridonova, E.A., 2016. Ocenka stoimosti biznesa [Valuation of business]. Tutorial and case studies. Moscow: Youright, 299 p.

Troshin, A.N. Burdina, A.A., and Razzhevaikin, D.V., 2012. Tekhnologiya ocenki innovacionnoj aktivnosti predpriyatij aviacionnoj otrasli [Technology to assess innovative activity of the aviation industry enterprises]. Monograph, Moscow: MAI, 176 p.

Troshin, A.N., Burdin, A.A., Moskvicheva, N.V., Tarasova, E.V., and Nikulina, E.N., 2016. Finansovyj menedzhment [Financial management]. Tutorial. Moscow: INFRA-M, 331 p.

Troshina, A.N., Burdina, A.A., Moskvicheva, N.V., Nikulina, E.N., Tarasova, E.V., and Rogulenko, T.M., 2016. Mechanism to analyze economic reliability of the innovational potential of aircraft enterprises. International Journal of Applied Business and Economic Research, 14, 747-765.

Upravlenie riskami innovacionnogo proekta [Risk management of innovation project], 2009. Institute of Regional Economics and Management. St. Petersburg. Retrieved 17.04.2017 from http://works.doklad.ru/view/ yFH0PTAv4ds/all.html

1. Moscow Aviation Institute (State University of Aerospace Technologies), 4 Volokolamskoje Shosse, Moscow 125993, Russia

2. Moscow Aviation Institute (State University of Aerospace Technologies), 4 Volokolamskoje Shosse, Moscow 125993, Russia

3. Moscow Aviation Institute (State University of Aerospace Technologies), 4 Volokolamskoje Shosse, Moscow 125993, Russia.  E-mail: moskvichevanatalia@mail.ru