

Vol. 38 (Nº 49) Year 2017. Page 6
A. A. NABOKIKH 1; E. A. BARMINA 2; A.V. RYATTEL 3; N. YU. FADEEVA 4; E. K. CHERANEVA 5
Received: 12/06/2017 • Approved: 30/06/2017
ABSTRACT: The purpose of the study is to analyze the approaches and methods of modeling the production using the adequate tools for describing economic and production processes that are most affordable and understandable for the producer. In particular, mathematical modeling helps identify and describe the most important and significant links between economic entities and to evaluate production parameters. The most efficient tool for mathematical modeling is production functions that allow to perform analytical calculations, to determine the efficiency of resource use and the appropriateness of their additional involvement in production, to forecast the output volume and to control the actuality of scheduled projects. An important aspect is the use of production functions in the planned estimates of the promising sectors in the regions that lack natural resources and raw materials for the development of the economy. |
RESUMEN: El propósito del estudio es analizar los enfoques y métodos de modelar la producción utilizando las herramientas adecuadas para describir los procesos económicos y de producción que son más asequibles y comprensibles para el productor. En particular, el modelaje matemático ayuda a identificar y describir los vínculos más importantes y significativos entre las entidades económicas y a evaluar los parámetros de producción. La herramienta más eficaz para el modelado matemático son las funciones de producción que permiten realizar cálculos analíticos, determinar la eficiencia del uso de los recursos y la idoneidad de su participación adicional en la producción, para pronosticar la salida volumen y controlar la actualidad de los proyectos programados. Un aspecto importante es el uso de las funciones de producción en las estimaciones previstas de los sectores prometedores en las regiones que carecen de recursos naturales y materias primas para el desarrollo de la economía. |
The socio-economic position of most of the agrarian regions in Russia remains unsatisfactory. This negatively affects the state of the budgetary system of the country and impedes the development of such territories, because agriculture is closely connected with nature, in particular with land, which is the main means of production; as a result, the production process mainly depends on seasonality and biological processes.
The competent use of the natural resource potential can be a starting capital for achieving higher strategic goals and emergence of new technology (Soboleva, 2013). In accordance with traditional ideas about economic development, the sources of the region's well-being are land, natural resources, geographic location, cheap labor resources and production facilities. However, the availability of natural resources, cheap labor, financial and technological resources is not sufficient to provide advantages in the competitive struggle on the global market. (Sosunova, 2010).
In this regard, a need emerges to search for industry sectors that are successfully developing during periods of decline in agriculture production. Mushroom production can be such a sector. The world's population consumes about 6.5 million tons of mushrooms annually, of which 6 million is produced on specialized mushroom farms. Average annual increase in the production of cultivated mushrooms in the world amounted to 11.8% over the past half-century.
Mushrooms are very popular in Russia, they are a national Russian product. An average Russian consumes at least 3 kilograms of mushrooms over a calendar year, of which about 1.04 kilograms are cultivated. For comparison, this figure in the USA and in France amounts to 2.5 kilograms, average figure in Europe is slightly more than 2 kilograms. At the same time, while the lion's share of mushrooms in the far abroad is grown in beds and on special shelves, the share of cultivated mushrooms in Russia accounts for about 30% of the total consumption of this product. However, the Russian Federation has seen an increase in the production of fresh cultivated mushrooms over the past few years.
One of the problems of managing enterprises in difficult market conditions is making timely and proper decisions in relation to the ongoing transformations in the economic situation. Methods of economic and mathematical modeling can be the methods of working out a solution to this problem.
The use of modeling for examination of socio-economic activities and evaluation of the parameters of its implementation is both a method of research and a method of solving economic problems (Nigmedzyanov, 2011).
The real world of the economy is very complex and diverse, and the system of economic and mathematical models of the appropriate level of complexity and variety is needed to reflect it adequately and to manage it efficiently, according to the famous Ashby’s law of requisite variety (Varyukhin, 2014). Production functions lie in the basis of modeling the activities of various types of production structures and systems, starting with individual enterprises and organizations to regions, industries and the economy of the country in general.
The importance of production functions in the construction of production models was covered in the works of domestic authors, such as Terekhov L.L. (Terekhov, 1974), Kleiner G.B. (Kleiner, 1986), Barkalov N.B. (Barkalov, 1981), Anchishkin A.I. (Anchishkin, 1973), Emelyanov A.S. (Emelyanov, 1980), Plakunov M.K. (Plakunov, 1984) and some others.
The framework of production functions allows to assess the productivity of resources used in the production process, to forecast economic growth, to form a modification of the production development scenario and optimization of the operation of the economic entity subject to a predetermined criterion and available resource constraints.
Due to this, sufficiently high requirements must be applied to the definition of the function type, the information used and the methods for their processing regarding the objectivity of recreating the genuine laws of social production.
Production function is an economic and statistical model of the production process in any economic system and reflects a stable economic quantitative relationship between the resource volume indicators and output. The relationship between the resource costs and volume of output is representative and relatively stable for economic systems of any level, if there are no significant changes in the production technology. Display and quantitative determination of this dependence forms the economic content of the concept of the production function.
In general form, the production function is the following: , where y is output, are production regressors (factors). Output y is the cumulative result of operation of all factors of production taken into consideration.
By now, considerable practice of building production functions for various objects has been accumulated (Kleiner, 1986); (Lotov, 1986). Depending on the scope of the object under study, implemented production technology and the interchangeability of production factors, various functions can be used.
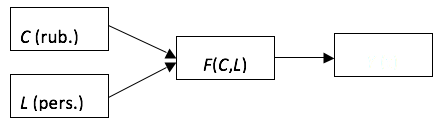
At the start of the study, let’s consider a two-factor production function with extremely aggregated characteristics. For the production under study, let’s take it as the PF with one output – production output (Y) – and two input actions – the costs of capital (C) and labor (L) resources. Structurally, such an aggregated model of a mushroom farming enterprise is presented in Figure 1.
Figure 1.
Structural representation of the model of a mushroom farming enterprise .
The formalized two-factor PF in its general form is defined by the dependence
------
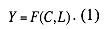
A two-factor homogeneous Cobb-Douglas production function with extremely aggregated characteristics was initially chosen as a model:
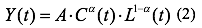
In Formula (2), A is a ratio describing the scale efficiency of the system. The larger value of the parameter A at fixed values of production factors corresponds to a larger value of Y(t). Consequently, the production process described by such a function is more efficient. Besides, A is a ratio that takes into account the influence of factors not included in the equation of the production function. The values a and b=1-aare the sensitivity (elasticity) functions, which describe the relative contribution of capital and labor to mushroom production. Ratios a and bshow how much in percentage the successive factor will change on average with the value of the corresponding factor changing by 1% at the invariability of the influence of other factors.
The Cobb-Douglas function is most often used to describe medium-scale economic entities described by stable and sustainable operation, when the involvement of an additional unit of the resource brings an effect proportional to the average productivity of the available resource.
A known method of revealing the indicators of the production function is application of the original statistical data in natural units of measurement. However, in the past, calculations showed that the error in the values of the scale ratios А can be several orders of magnitude. This is why the initial data in dimensionless form were used in addition to absolute units. Reduction to the latter was made by bringing the time series to the first year of the identification interval. Besides, the model identification and calculations have been performed for unsmoothed and smoothed initial data. Smoothing was performed using the method of moving average by three points in order to eliminate the effect of random runouts.
To ensure statistical reliability at the evaluation of multiple regression, it is required that the number of observations is at least three times the number of parameters evaluated (Zamkov, 1999). The production function was identified by the method of minimization of the mean square deviation of model dependencies from empirical data.
The production function (Formula 2) reduces to a linear function:
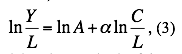
Its parameters were evaluated by the method of least squares. The quality of the models and their parameters was determined by the values of the multiple correlation ratio R, determination coefficient R2, Student t-test, Fisher F-test.
Mathematical modeling is shown by the example of operation of mushroom growing in the Kirov region for 2004-2013 based on the actual initial data (Table 1). The annual volume of cultivated mushrooms produced in the Kirov region (in tons) was taken as the production indicator; the value of fixed assets at full cost (in actual prices at the end of the year) (in thousand rubles) was taken as the indicator of capital resources; the "labor resources" indicator is understood as the average annual number of industrial and production personnel. The mathematical processing of the empirical data was carried out using the "Regression" analysis tool of the Microsoft Excel software.
Table 1
Indicators of the market of mushroom growing in the Kirov region
Indicators |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
Value of fixed assets at full book value (in actual prices at the end of the year) thous. rub. |
1,650 |
1,780 |
2,470 |
3,800 |
3,260 |
4,610 |
5,070 |
4,400 |
4,830 |
6,420 |
Headcount of industrial production personnel or a number of manhours worked |
14 |
16 |
18 |
18 |
18 |
25 |
25 |
20 |
20 |
25 |
Volume of production (tons) |
2 |
5 |
8 |
6 |
89 |
139 |
156 |
143 |
138 |
158 |
Capital investment per unit |
825 |
356 |
308.75 |
633.333 |
36.6292 |
33.1655 |
32.5 |
30.7692 |
35 |
40.6329 |
Personnel per unit |
7 |
3.2 |
2.25 |
3 |
0.202 |
0.179 |
0.160 |
0.139 |
0.144 |
0.158 |
Results of evaluation of the parameters and quality of models of the homogeneous Cobb-Douglas production function at a significance level of 5% are presented in Table 2.
Table 2.
Results of evaluation of the parameters and quality of models of the homogeneous Cobb-Douglas production function
Model parameters and ratios |
Data in natural units |
Unsmoothed data (dimensionless form) |
Smoothed data (dimensionless form) |
А |
4.0986E-10 |
2.07283 |
1.38748969 |
a |
4.27682682 |
4.276827 |
5.667408 |
R |
0.77950062 |
0.779501 |
0.91934019 |
R2 |
0.60762121 |
0.607621 |
0.845186 |
P-value А |
0.009064 |
0.269498 |
0.5215 |
P- valuea |
0.007849 |
0.007849 |
0.001234 |
F |
12.38846 |
12.38846 |
32.75628 |
Significance of F |
0.007849 |
0.007849 |
0.001234 |
High values of the multiple correlation ratio indicate a fairly close relationship between the function and all the factor-arguments included in the model. The coefficient of determination (especially in the case of smoothed data) indicates a fairly complete coverage of all the factors that significantly influence the function by the resulting model. Other factors account for 8.1% only.
If the probability (significance of F) is less than a given level of significance, then the hypothesis that regression is insignificant (i.e. the hypothesis that all the coefficients of the regression function are equal to zero) is rejected and regression is considered significant. In our case, regression is significant in all models.
Significance levels corresponding to the values of the criterial characteristics are calculated in the P-Value column. If the calculated level of significance is less than a given level, the hypothesis of a significant difference from zero is assumed; otherwise, the hypothesis of an insignificant difference of the ratio from zero is assumed. In our case, ratio A insignificantly differs from zero in the second and third models.
The obtained ratios indicate that the homogeneous production function ![]() poorly describes the analyzed processes of mushroom growing, the models do not possess the required approximative properties, and therefore are not suitable for describing the operation of the mushroom farming enterprise over the period under consideration.
poorly describes the analyzed processes of mushroom growing, the models do not possess the required approximative properties, and therefore are not suitable for describing the operation of the mushroom farming enterprise over the period under consideration.
Then the possibilities of modeling the system operation on the basis of the two-factor inhomogeneous Cobb-Douglas production function were studied:
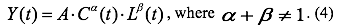
The production function (Formula 4) reduces to a linear function, the parameters of which were assessed using the method of least squares:
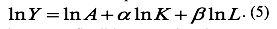
The cited dependence has more flexible approximative properties, since it has three adaptive adjusting parameters: А,a,b. The parameters of model (2) were identified in a way similar to the homogeneous Cobb-Douglas PF.
The obtained numerical characteristics of the models for the inhomogeneous Cobb-Douglas production function are shown in Table 3.
Table 3
Numerical characteristics of the models for the inhomogeneous Cobb-Douglas production function
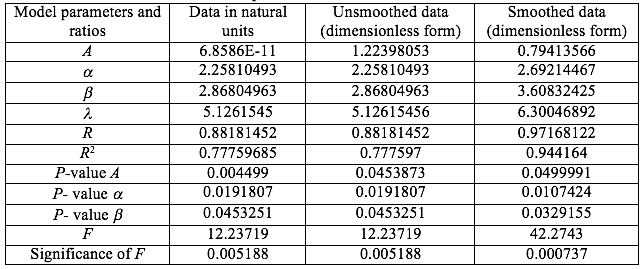
Statistical parameters of the quality of approximation cited in Table 3 show that the descriptive properties of model (2) have improved in comparison with the model (1): the determination coefficient has increased, and the adequacy of models has increased.
The values of a and b for the mushroom growing sector in the Kirov region are rather high both in Table 2 and Table 3, which indicates the efficient use of both capital and labor resources. The change in the output of mushroom products is more sensitive to changes in the volume of the use of labor as a production factor.
In addition to the factorial elasticities a and b, Table 3 provides the values of the total elasticity l=a+b, which describes the integral, scale efficiency of mushroom production. Since l>1, there is an increasing return on scale.
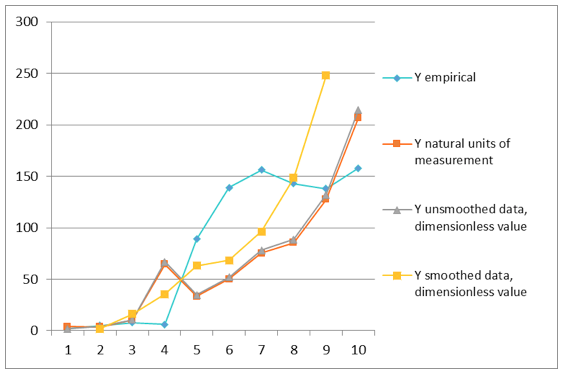
Charts of real and model trajectories are shown in Figures 2 and 3.
According to the model (Table 3), smoothed data, dimensionless form, the average capital productivity and average labor productivity are calculated, which show how many tons of cultivated mushrooms account for 1 thous. rub. of fixed assets and 1 manhour of labor spent. The marginal capital productivity and marginal labor productivity show how much in additional tons the production of cultivated mushrooms will increase, if the volume of the corresponding production factor grows by one unit, while the others remain unchanged.
Figure 2
Charts of real and model data for the homogeneous Cobb-Douglas production function
------
Figure 3
Charts of real and model data for the inhomogeneous Cobb-Douglas production function
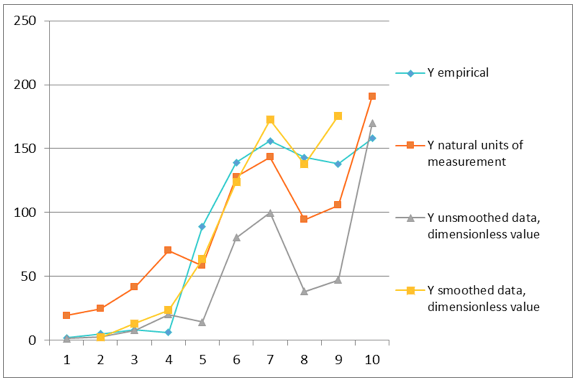

Table 4
Numerical characteristics of the model

As can be seen from Table 4, the equation (Formula 7) is very significant according to F-test, as well as its parameters by t-test. The coefficient of determination is high. As a result, the change in the output of finished mushroom growing production is explained by the built model by 86%, depending on the resource costs and the influence of STP (3).
The efficiency of using labor and capital resources is high, just like in models (1) and (2). The positive value of the parameter g indicates the modern technology in this sector.
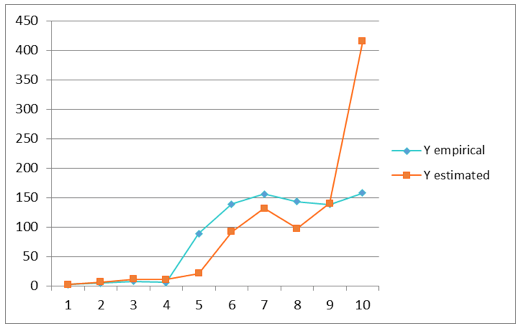
The charts of the modeled production function (Formula 7) and the actual output of mushroom growing production are shown in Fig. 4.
Figure 4
Charts of the actual and model data for the Cobb-Douglas PF with STP
Leontiev's production function can also be used to describe the operation of the mushroom farming enterprise. This function is intended for modeling a strictly deterministic technology that does not allow deviation from technological norms of resource use per unit of output. It is normally used to describe small-scale or fully automated production facilities.
Leontiev’s function is as follows:
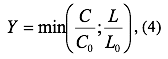
where the ratios C0 и L0express the amount of the corresponding resource required for the production of the product unit. Estimations showed that C0=233.178 thous. rub., L0=1.644 manhour.
There is a constant return on scale when using the production function (4). Elasticity of factor replacement for any resource in such a model is equal to zero.
Complex and very complex production facilities such as "black boxes" can be studied using the method of production functions. The concept of "black box" is widely used in cybernetics in the study of processes of managing complex systems. In this case, objects whose detailed structure is excessively complex or unknown to the researcher are considered complex or very complex systems (Gorbunov, 2014).
At present, mathematical models and methods are an essential element of the modern economic science, both at the micro- and macrolevel. Economic and mathematical methods and models are designed to help realize the current situation on the market of agricultural products and choose adequate tools for its regulation.
Particular complexity of agricultural production lies in the intertwining of economic processes with biological processes. Dependence on natural factors makes reproduction in agriculture more stochastic than in any other field of the national economy.
Enterprises in the agricultural sector can introduce economic and mathematical models to project the mushroom production. The most important provisions for the design of programs for the development of mushroom farming on the principles of economic and mathematical models presented in the paper are intended for use at any economic entity producing cultivated mushrooms; all it requires is to generate the original model parameters in a suitable manner.
Manufacturers are interested in maximizing the use of resources in production. Consequently, the production function reflects the dependence of the maximum possible production output from the resources invested in production, because the function determines principal limits of the maximum possible output.
It was determined that the combination of any involved resources contributes to the maximum possible production output, but at the same time, producers aim to reduce costs by replacing expensive resources with cheaper ones. Production is impossible in case of the absence of at least one resource, i.e. there is no output. The production function allows to reflect the dependence of production output on the use of resources in case of their most efficient use. The production function links production output to the use of interchangeable resources. With a fixed volume of output, the nature of substitution of one resource by other has its own specifics, it depends on the type of the production being modeled. A change in the output may occur simultaneously with the replacement of resources. Therefore, a specific formula of the production function should properly reflect the specificity of the increase in output and replacement of resources for each type of production.
Anchishkin, A., 1973. Prognozirovaniye rosta sotsialisticheskoy ekonomiki [Forecasting the growth of the socialist economy]. Moscow: Economics.
Barkalov, N., 1981. Proizvodstvennyye funktsii v modelyakh ekonomicheskogo rosta [Production functions in the models of economic growth]. Moscow: Publishing house of the Moscow University.
Varyukhin, A., 2014. Modelirovaniye ekonomicheskikh protsessov [Modeling of economic processes], Saratov: unnumb.
Gorbunov, V., 2014. O razmernostnoy probleme v ekonomike: proizvodstvennaya funktsiya kak psevdo-chernyy yashchik [Concerning the dimensional problem in the economy: a production function as a pseudo black box]. Journal of the economic theory, 4, 199-212.
Emelyanov, A., 1980. Obshchestvennoye proizvodstvo: dinamika, tendentsii, modeli [Social production: dynamics, trends, models]. Kiev: Nauk, dumka.
Zamkov, O., 1999. Matematicheskiye metody v ekonomike [Mathematical methods in economics]. Moscow: Business and service.
Kleiner, G., 1986. Proizvodstvennyye funktsii: Teoriya, metody, primeneniye [Production functions: Theory, methods, use]. Moscow: Finance and statistics.
Lotov, A., 1986. Vvedeniye v ekonomiko-matematicheskoye modelirovaniye [Introduction to the economic and mathematical modeling]. Moscow: Nauka.
Nigmedzyanov, E.S., 2011. Algoritm informatsionnogo modelirovaniya proizvodstvennykh protsessov promyshlennogo klastera [Algorithm of informational modeling of production processes in an industrial cluster]. Branch-wise economics, 8 (32), 34
Plakunov, M.R.R., 1984. Proizvodstvennyye funktsii v ekonomicheskom analize [Production functions in economic analysis]. Vilnius: Mintis.
Soboleva, O., 2013. Kompleksnaya otsenka prirodno-resursnogo potentsiala regiona [Comprehensive assessment of the natural and resource potential of the region]. Regionology, 1, 52-55.
Sosunova, L.S.E., 2010. Ekonomiko-matematicheskoye modelirovaniye razvitiya regionalnoy ekonomiki [Economic and mathematical modeling of the development of the regional economy]. Bulletin of the Samara State University of Economics, 7(69), 90-96.
Terekhov, L., 1974. Proizvodstvennyye funktsii [Production functions]. Moscow: “Statistics”.
1. FSBEI HPE "Vyatka State University", 610000, Russia, Kirov, Moscovskaya str. 36. E-mail: alex_nabokih@mail.ru
2. FSBEI HPE "Vyatka State University", 610000, Russia, Kirov, Moscovskaya str. 36.
3. FSBEI HPE "Vyatka State University", 610000, Russia, Kirov, Moscovskaya str. 36.
4. FSBEI HPE "Vyatka State University", 610000, Russia, Kirov, Moscovskaya str. 36.
5. FSBEI HPE "Vyatka State University", 610000, Russia, Kirov, Moscovskaya str. 36.