ISSN 0798 1015

Vol. 38 (Nº 43) Año 2017. Pág. 34

Uso do software WebPROA para resolver problemas usando métodos Ordinais Multicritério: um exemplo da determinação do tamanho relativo das empresas brasileiras de distribuição de energia elétrica

Ordinal Multicriteria Methods using WebPROA: An application to the relative size of Brazilian electrical distributors

Mirley Bitencourt FERREIRA 1; Lidia ANGULO-MEZA 2; Maria Helena Campos SOARES DE MELLO 3; João Carlos Correia Baptista SOARES DE MELLO 4

Recibido: 04/05/2017 • Aprobado:21/06/2017

Conteúdo

1. Introdução

2. Os métodos de Borda, Condorcet e Copeland

3. Implementação computacional: o software WebPROA

4. Exemplo numérico: distribuidoras brasileiras de energia elétrica

5. Comentários Finais

Agradecimentos

Referências bibliográficas

1. Introdução

Na literatura são citados três principais métodos ordinais de apoio multicritério à decisão: Borda(Borda, 1781), Condorcet (Condorcet, 1785) e Copeland (Copeland, 1951). Como mostrado em (Barba-Romero & Pomerol, 1997), esses métodos caracterizam-se por fazer uma ordenação geral levando em conta ordenações parciais. Esses métodos tem a grande de vantagem na simplicidade e de exigir pouco informação do decisor. Assim, devem ser usados apenas em situações em que há apenas informação ordinal o que os torna especialmente uteis em avaliação esportiva (Kladroba, 2000; J. C. C. B. Soares de Mello, Gomes Júnior, Angulo-Meza, & Mourão, 2015; J. C. C. B. Soares de Mello, Gomes, Gomes, & Soares de Mello, 2005) . Apesar da sua maior utilização ser em esportes, são eventualmente utilizados em outras áreas como agricultura (Oliveira et al., 2015; Valladares et al., 2008) e transportes (Caillaux, Sant´anna, Angulo-Meza, & Soares de Mello, 2011).

Embora os métodos utilizem métodos bastante simples, dependendo do número de alternativas e de critérios, a quantidades de cálculos a serem realizados podem ser muito grande, i.e., são computacionalmente intensos. Isso é especialmente verdade para os métodos Condorcet e Copeland, por exigirem comparações pareadas entre todas as alternativas. Desta forma, resulta muito útil dispor de uma ferramenta computacional para a execução destes métodos.

Sendo assim este artigo tem como objetivo principal apresentar uma ferramenta computacional dos mencionados métodos, chamada WebPROA. Para tal serão apresentados os métodos e explicada a implementação computacional. De forma a ilustrar o uso do software e como segundo objetivo, será aplicado o Web PROA a um exemplo para avaliação do tamanho relativo de companhias distribuidoras de energia elétrica. Cabe destacar que este software encontra-se disponível na web de forma gratuita (www.webproa.com)

Este artigo está organizado da seguinte forma. Na próxima seção, seção II, são descritos os métodos ordinais de Borda, Condorcet e Copeland. Na seção III é explicada a implementação computacional destes métodos chamada de WebPROA. Em seguida, na seção IV, são utilizados dados das companhias brasileiras de distribuição de energia elétrica para a ilustrar o uso do WebPROA, Finalmente, na seção V são apresentados os comentários finais.

O primeiro destes métodos, o método de Borda, proposto por Jean Charles de Borda (1733-1799), é um método que utiliza uma escala ordinal, estabelecida pelos decisores, e as alternativas ganham uma ordenação por meio de pontuação. Essa pontuação é dada da seguinte forma: as alternativas são ordenadas da melhor para a pior segundo cada critério. A cada posição da alternativa é atribuída uma pontuação correspondente (1º lugar = 1 ponto; 2º lugar = 2 pontos; e assim sucessivamente; em caso de empate é realizada uma média dos pontos e atribuída para cada alternativa). Os pontos atribuídos pelos decisores a cada alternativa são somados (pré-ordem agregada) e a alternativa que tiver obtido a menor pontuação é a escolhida (Dias, Almeida, & Climaco, 1996; E. G. Gomes, Soares de Mello, Abreu, Carvalho, & Zen, 2013).

O contemporâneo de Borda, Marie Jean Nicolas de Caritat, marquês de Condorcet (1743-1794), conhecia os trabalhos do de Borda e criticava-os pelo fato que a inclusão ou exclusão de alternativas podia alterar a ordenação final. Mais tarde essa característica viria ser conhecida como a violação do axioma da independência em relação às alternativas irrelevantes (Arrow, 1951). Para contornar esse problema o Condorcet desenvolveu um método sobre agregação de preferências sob uma visão de votação que ficaria conhecido como método de Condorcet.

Neste método, as alternativas são comparadas sempre duas a duas e constrói-se uma matriz que expressa a relação entre elas, chamada de matriz da relação de Condorcet ou abreviadamente matriz de Condorcet. Os elementos da matriz C são definidos como em (1).

Se Ai P Ak, então, cik = 1; se Ai = Ak, então, cik = 0; senão cik = -1             (1)

onde P expressa a preferência de uma alternativa sobre outra.

Ainda para construir a matriz C todos os pares de alternativas devem ser comparados em todos os critérios. Dado que o número de comparações entre um dado par de alternativas é igual ao número de critérios, o total de comparações a ser feito é dado por (2).

Onde NC é o número total de comparações; n é o número total de alternativas e m o número total de critérios.

Uma vez obtida a matriz, a ordenação é feita utilizado técnica de ordenação descendente (Dias et al., 1996), de melhor para pior, sendo a primeira colocada aquela que domina a todas as outras alternativas. A segunda colocada é aquela que domina a todas as outras quando a primeira é retirada do problema. Uma alternativa i domina todas as outras se, com exceção da diagonal principal, tem cik = 1, " k≠i. De forma análoga, pode se utilizar uma técnica de ordenação ascendente, começando-se por ordenar a alternativa que é dominada por todas as outras e fica em último lugar. Essa alternativa é retirada e o procedimento se repete. Uma alternativa i é dominada por todas as outras se tem cki = 1, " k≠i.

Existem casos em que nenhum dos procedimentos de ordenação consegue estabelecer uma ordenação total de alternativas. Isto se deve a existência dos chamados ciclos de intransitividade. Esta ocorrência é conhecida como Paradoxo de Condorcet. Na Figura 1 apresenta-se um exemplo deste ciclo para três alternativas A, B e C. Assim, observa-se que A é preferível a B, B é preferível a C e C é preferível A, sendo que não é possível estabelecer uma preferência entre as três.

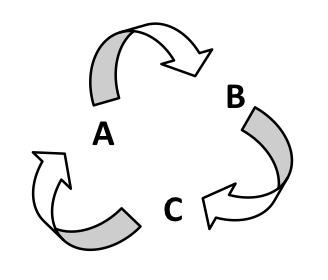
Figura 1. Ciclo de Intransitividade.

Observa-se assim que o método de Condorcet elimina o problema da não independência em relação às alternativas irrelevantes, porém introduz um outro problema, o da possível existência de ciclos de intransitividade, não respeitando, portanto, os axiomas de Arrow. Quando os ciclos de intransitividade não aparecem, e deseja-se obter uma pré-ordem total (fazer uma ordenação completa admitindo-se a possibilidade de empate), o método de Condorcet deve ser preferido ao de Borda (M. H. C. Soares de Mello, Quintella, & Soares de Mello, 2004).

Quanto ao método Copeland, ele usa a mesma matriz do método de Condorcet e foi criada na tentativa de resolver simultaneamente os problemas do método de Borda e do Condorcet. Neste método, para cada alternativa soma-se o conteúdo dos elementos da linha da matriz (3).

A alternativa i melhor colocada é aquela que apresentar maior Vi. Este método elimina o problema do Paradoxo de Condorcet e é menos dependente das alternativas irrelevantes que o método do Borda. Deve-se observar que quando o método de Condorcet não apresenta ciclos de intransitividade o método de Copeland fornece o mesmo resultado do método de Condorcet. Na existência de ciclos de intransitividade, a ordenação realizada pelo Condorcet fora dos ciclos é preservada no método de Copeland. Assim, em muitas situações o método de Copeland é o indicado para usar quando se dispõe apenas de informação ordinal. Deve-se realçar que não existe método ordinal perfeitamente junto, isto é, que atenda todos os axiomas do Arrow (Arrow, 1951). Caso se deseja evitar os problemas dos métodos ordinais é necessário usar escalas cardinais que exigem maior informação dos decisores, como visto por exemplo em (Bana e Costa, Angulo-Meza, & Oliveira, 2013).

Mais detalhes sobre os métodos ordinais podem ser encontrados em (Barba-Romero & Pomerol, 1997; Bou & Soares de Mello, 2015; Dias et al., 1996; C. F. S. Gomes, Gomes, & Almeida, 2006; L. F. A. M. Gomes, Araya, & Carignano, 2004) .

A implementação computacional é denominada de Web PROA – PReferências Ordinais Agregadas. Este software utiliza um sitio web (www.webproa.com) para entrada de dados.

O Web PROA foi desenvolvido em Java, JSP, JavaScript e HTML através da plataforma de desenvolvimento NetBeans. Java (Lindholm, Yellin, Bracha, & Buckley, 2013) é uma linguagem de programação orientada a objetos criada na década de 90 pela empresa Sun Microsystems e uma de suas principais características é ser multiplataforma. Esta característica é possível por conta da Máquina Virtual Java (do inglês Java Virtual Machine – JVM) que é um programa que executa os aplicativos Java, pois, converte os bytecodes em um código executável. Outro benefício dessa linguagem é ser código aberto, assim, não existem custos para desenvolver uma implementação computacional nesta linguagem.

Java Server Pages (JSP) é uma tecnologia Java empregada para desenvolver aplicativos na web baseada na linguagem Java e também é multiplataforma e de código aberto. Através desta ferramenta é possível capturar informações presentes em um formulário, manipular arquivos, fazer conexões a banco de dados, obter informações sobre o usuário, entre outros. Essa tecnologia permite a interação de marcações dinâmicas através do código Java com marcações estáticas que são compiladas num servidor gerando páginas HTML. Os servidores compatíveis com esta tecnologia são Tomcat e Glassfish.

Neste trabalho foi utilizado o Glassfish que tem a vantagem de ser uma aplicação de código livre escrita em Java e que suporta a tecnologia JSP e diversas outras de serviços web. Este servidor está embutido na plataforma de desenvolvimento (do inglês Integrated Development Environment – IDE) Netbeans. Esta plataforma é gratuita e fornece suporte para desenvolvimento de softwares em Java, PHP, JavaScript, etc. Também oferece aos desenvolvedores diversas ferramentas como escrever, identificar bugs e compilar as quais facilitam a criação de programas e sistemas que podem ser executados em computadores, em dispositivos móveis e empresariais. Seus principais recursos são: editor de código fonte que reconhece comandos da linguagem que se destacam das demais partes do código, visualizador de classes Java (neste caso), ajuda off-line e on-line, auto-completa comandos. As linguagens de programação Java e JSP e as ferramentas Netbeans e Glassfish são disponibilizadas, atualmente, pela empresa Oracle.

JavaScript é uma linguagem de programação de script, mas não é baseada na linguagem Java. Um código script não necessita ser processado (ou compilado) antes de ser executado. No contexto web, o JavaScript é executado quando a página é carregada ou quando é acionado um evento pelo usuário. Esta linguagem torna a página web dinâmica permitindo que mesmo sem ser recarregada o seu conteúdo possa ser modificado. Finalmente, HTML (HyperText Markup Language) é uma linguagem de marcação utilizada para publicar páginas Web estáticas que são interpretadas nos navegadores. Essas duas últimas linguagens (JavaScript e HTML) são padrões da W3C. A W3C, abreviação do inglês World Wide Web Consortium, é um consórcio internacional que estabelece padrões para desenvolvimento de páginas web.

A implementação do WebPROA teve duas fases. Na primeira, o foco foi a implementação dos algoritmos dos métodos Borda, Condorcet, Copeland de forma funcional. Estes algoritmos foram implementados em JAVA. As alternativas, os critérios e os valores de cada alternativa e cada critério são os parâmetros de entrada de dados de um arquivo no formato CSV e o resultado apresentado em páginas HTML. Na segunda fase foi desenvolvido um programa Web com o objetivo de aumentar a facilidade de uso por parte do usuário.

Para executar o programa web é requerido um sistema operacional com interface gráfica tal como Windows XP, Windows 7, Windows Vista, Mac OS, Linux Ubuntu e etc; e conte com um navegador de internet (Mozilla, Chrome, Internet Explorer, Safari, etc).

Para ilustrar o uso do WebPROA ele será utilizado para avaliar o tamanho das distribuidoras de energia elétrica no Brasil.

A distribuição de Energia Elétrica no Brasil é uma concessão do Estado e é fiscalizada pela ANEEL. A maior parte dos estudos sobre as distribuidoras são para avaliar a sua eficiência (Alves & Soares de Mello, 2015; Andrade, Alves, Silva, & Soares de Mello, 2014; Machado, Soares de Mello, & Roboredo, 2016; Moreno, Andrade, Angulo Meza, & Soares de Mello, 2015; Pereira De Souza, Diallo, Castro Souza, & Baidya, 2010; Pessanha, Souza, & Da Costa Laurencel, 2007; Tschaffon & Angulo Meza, 2014) . Um fato que é normalmente citado, mas raramente levado em conta é que as distribuidoras apresentam tamanhos bastante diferentes. Uma ordenação das distribuidoras pelo seu tamanho pode facilitar a formação de clusters para o cálculo de eficiências mais justas.

Assim, para avaliar o tamanho das distribuidoras foram selecionadas as mesmas distribuidoras usadas no artigo (Moreno et al., 2015),  que são as 20 empresas que atendem 96% do Mercado Brasileiro, em termos de potência distribuida (em Tera Watt hora). No entanto dentre as variáveis usadas neste artigo o OPEX é um indicador de despesa e não de tamanho, portanto não será utilizado. Desta forma, os critérios usados neste estudo de caso são Extensão da Rede (milhares de quilômetros), número de consumidores (em milhões) e consumo (TWH).

Para fazer o uso do WebPROA, precisa-se fazer a entrada de dados através de sua tela inicial, tal como mostrado na figura 2.

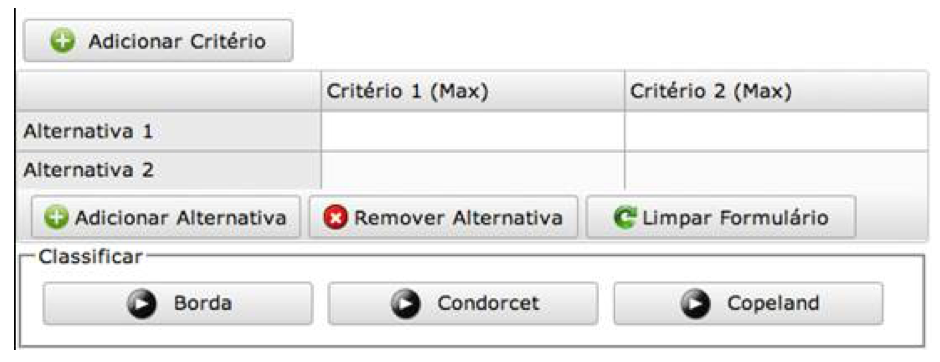
Figura 2. Tela inicial do WebPROA.

Nesta figura pode-se observar que a entrada de dados é realizada por meio uma matriz inicial com duas colunas (dois critérios) e duas linhas (duas linhas). Dispõe-se de botões para aumentar tanto o número de alternativas quanto o número de critério. Para editar a coluna do critério (j) basta clicar sobre o critério desejado e alterar o nome, e depois escolha se o critério será de maximizar (MAX) ou de minimizar (MIN). Para finalizar clique em “Salvar” (Figura 3).

Figura 3 – Exemplo de edição de critérios

No presente estudo de caso, todos os critérios são de maximização. A figura 4 apresenta os dados do estudo de caso já inseridos no WebPROA.

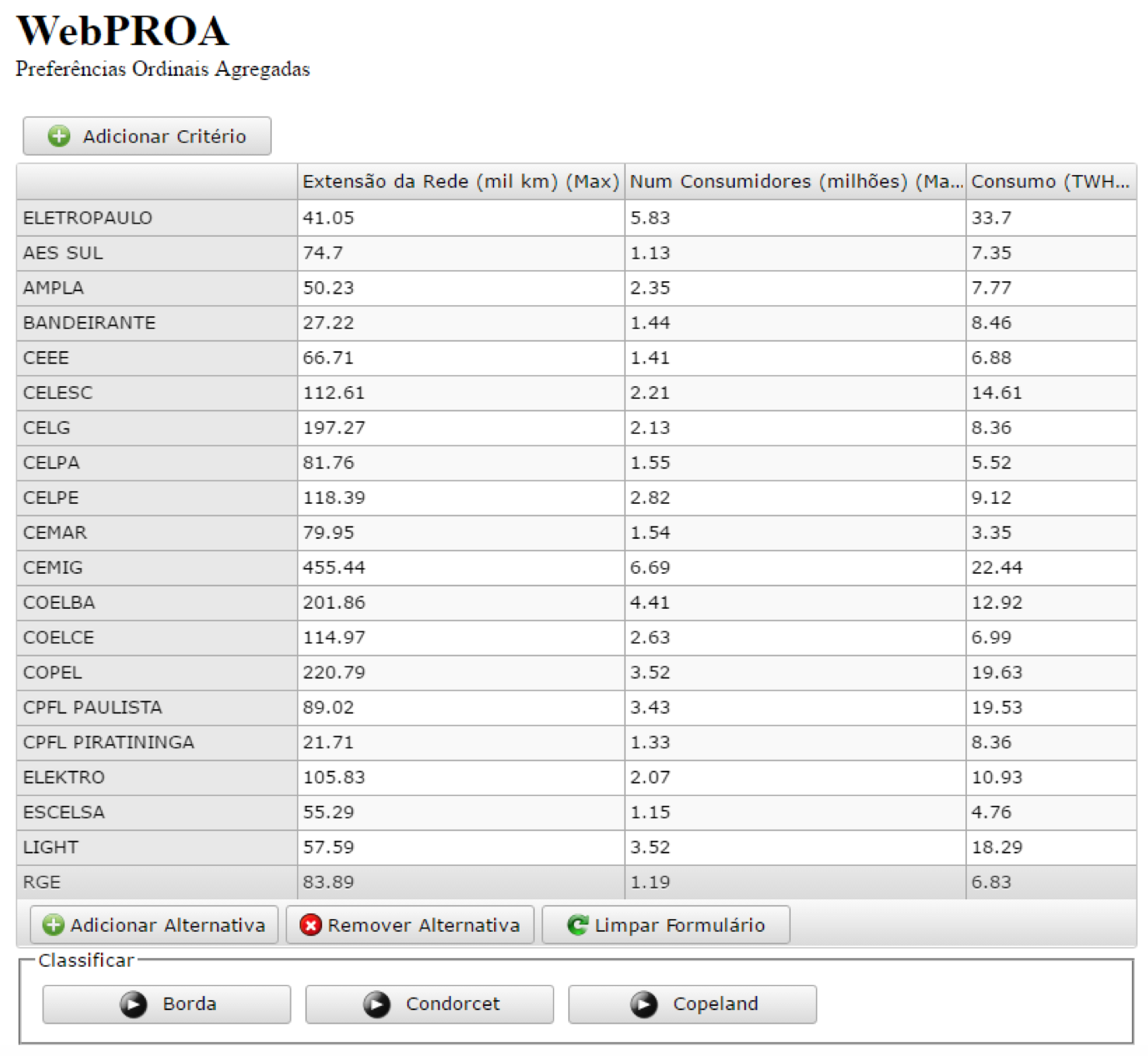
Figura 4. Tela do WebPROA com os dados do estudo de caso.

Para gerar os resultados basta clicar no botão do método desejado e o programa abrirá uma nova página HTML com o resultado da ordenação. Para o presente estudo de caso, a ordenação e as pontuações geradas utilizando o método de Borda são apresentados na Figura 5.

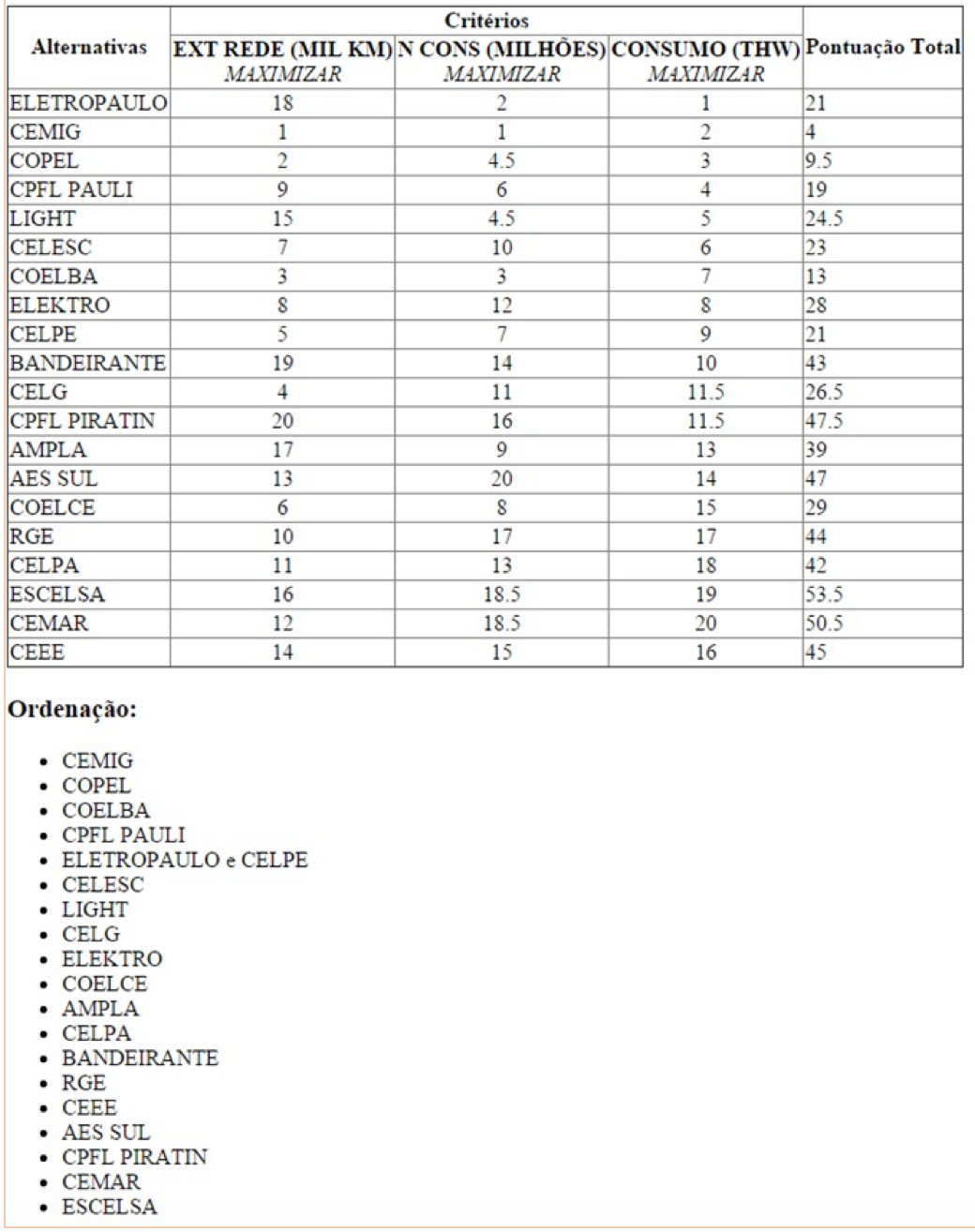
Figura 5 – Resultados para o estudo de caso usando o método de Borda

Neste estudo de caso não foram observados empates em nenhum critério, mas eles são facilmente pontuados pelo WebPROA.

Quando se escolhe o método de Condorcet é gerada uma matriz de Condorcet com os resultados das comparações entre cada par de alternativas, tal como descrito na seção II.  Também são realizadas as ordenações descente e ascendente. A Figura 6 apresenta o resultado fornecido pelo Método de Condorcet para o estudo de caso.

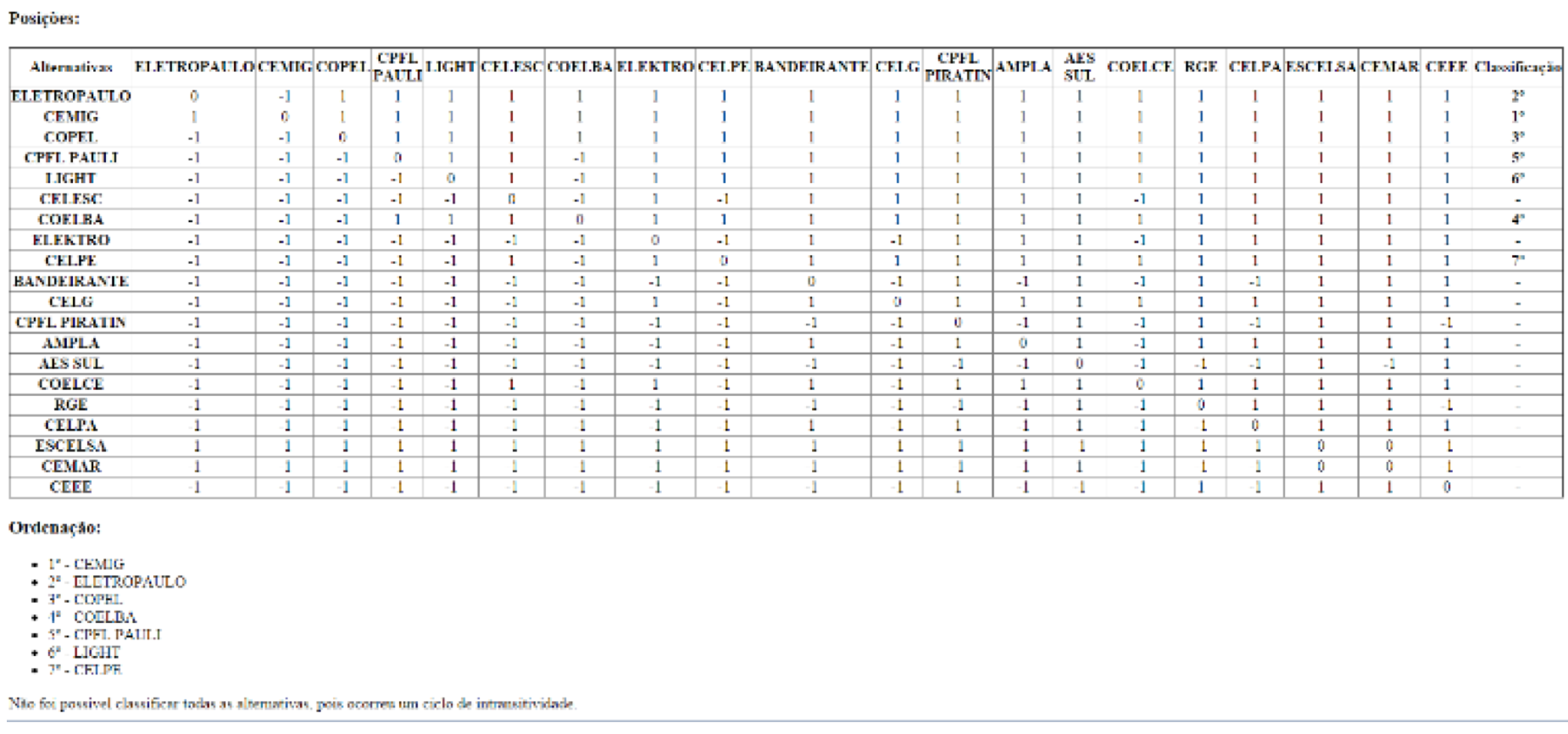
Figura 6 – Resultados para o estudo de caso usando o método de Condorcet.

Nesta figura pode-se observar que só foi possível ordenar 7 distribuidoras, pois houve um ou mais ciclos de intransitividade. Neste caso, o WebPROA informa que “Não foi possível classificar todas as alternativas, pois ocorreu um ciclo de intransitividade”. Caso não ocorresse o ciclo descrito acima o software iria apresentar a ordenação de todas as alternativas.

Usando o Método de Copeland obtém-se o resultado apresentado na figura 7. Tal como, a matriz utilizada pelo Método de Copeland é a mesma do método de Condorcet, apresentando ainda a “Pontuação Total” de cada distribuidor. Desta forma, é obtida uma ordenação total dos distribuidores.

Figura 7 - Resultados para o estudo de caso usando o método de Copeland

Em seguida, observando os resultados, por qualquer dos métodos utilizados a CEMIG foi a maior das empresas analisadas. Observa-se que ela supera as demais em todos os critérios, com exceção da EletroPaulo que a supera em quantidade de energia distribuída.

Este trabalho apresenta uma implementação computacional de três métodos ordinais multicritério: os métodos de Borda, Condorcet e Copeland. O software denominado WebPROA (PReferências Ordinais Agregadas) é gratuito, foi desenvolvido de forma que possa ser utilizado por qualquer usuário em qualquer plataforma com o uso de qualquer programa Web e pode ser encontrado em www.webproa.com.

A existência deste software permite que os pesquisadores que usam métodos ordinais, principalmente para problemas de grande porte, dediquem menos tempo à obtenção dos resultados e mais dediquem mais atenção à modelagem e implementação.

Este software tem sido validado comparando os resultados com os obtidos em estudos de caso na literatura. Os resultados são obtidos em um tempo computacional extremamente reduzido.

A interface gráfica do software na web permite uma melhor visualização das alternativas e dos critérios, e as opções de edição facilitam a visualização dos resultados.

Desenvolvimentos futuros incluem uma versão executável do programa, sem necessidade de acesso a internet, opções para salvar os dados e os resultados, e a sua adaptação para variantes dos métodos utilizados ou métodos ordinais mais complexos

Com relação ao exemplo numérico utilizado ele poderá vir a ser utilizado em conjunto com Análise Envoltória de Dados para avaliar a eficiência das distribuidoras de energia elétrica levando em conta seu porte.

 Agradecemos aos CNPq pelo apoio financeiro.

Alves, L. A., & Soares de Mello, J. C. C. B. (2015). Weights based clustering in Data Envelopment Analysis using Kohonen Neural Network: An Application in Brazilian Electrical Sector. IEEE Latin America Transactions 13, 188-194.

Andrade, G. N., Alves, L. A., Silva, C. E. R. F., & Soares de Mello, J. C. C. B. (2014). Evaluating Electricity Distributors Efficiency Using Self-Organizing Map and Data Envelopment Analysis. IEEE Latin America Transactions, 12(8), 1456-1464.

Arrow, K. J. (1951). Social Choice and Individual Values. New York: Wiley.

Bana e Costa, C. A., Angulo-Meza, L., & Oliveira, M. D. (2013). O método MACBETH e aplicação no Brasil. Engevista, 15(1), 3-27.

Barba-Romero, S., & Pomerol, J. C. (1997). Decisiones Multicriterio: Fundamentos Teóricos e Utilización Práctica: Universidad de Alcalá.

Borda, J. C. (1781). Memoire sur les Elections au Scrutin: Histoire de l'Académie Royale des Sciences.

Bou, Á. S. F., & Soares de Mello, J. C. C. B. (2015). Analysis of the multi-criteria decision-making veto method. Ingeniare, 23(4), 556-568.

Caillaux, M. A., Sant´anna, A. P., Angulo-Meza, L., & Soares de Mello, J. C. C. B. (2011). Container Logistics in Mercosur: Choice of a Transhipment Port Using Ordinal Copeland Method, Data Envelopment Analysis and Probabilistic Composition. Maritime Economics and Logistics, 13(4), 355-370.

Condorcet, M. J. N. d. C. M. d. (1785). Essai sur l'Application de l'Analyse à la Probabilité des Décisions Rendues à la Pluralité des Voix: Imprimerie Royale.

Copeland, A. H. (1951). A reasonable social welfare function: University of Michigan.

Dias, L. M. C., Almeida, L. M. A. T., & Climaco, J. C. N. (1996). Apoio Multicritério à Decisão. Coimbra: Universidade de Coimbra.

Gomes, C. F. S., Gomes, L. F. A. M., & Almeida, A. T. (2006). Tomada de Decisão Gerencial: O Enfoque Multicritério. São Paulo: Editora Atlas.

Gomes, E. G., Soares de Mello, J. C. C. B., Abreu, U. G., Carvalho, T. B. d., & Zen, S. d. (2013). Análise de Tipologias de Sistemas de Produção Modais de Pecuária de Cria pelo uso do Método Ordinal de Copeland. Pesquisa Operacional para o Desenvolvimento, 5(1), 43-57.

Gomes, L. F. A. M., Araya, M. C. G., & Carignano, C. (2004). Tomada de Decisões em Cenários Complexos. São Paulo: Pioneira Thompson Learning.

Kladroba, A. (2000). Das aggregations problem bei der erstellung von rankings: Einige anmerkungen am beispiel der Formel 1 weltmeisterschaft 1998. Jahrbucher fur Nationalokonomie und Statistik, 220(3), 302-314.

Lindholm, T., Yellin, F., Bracha, G., & Buckley, A. (2013). The Java® Virtual Machine specification. Redwood City: Oracle America.

Machado, L. G., Soares de Mello, J. C. C. B., & Roboredo, M. C. (2016). Efficiency Evaluation of Brazilian Electrical Distributors Using DEA Game and Cluster Analysis. IEEE Latin America Transactions, 14(11), 4499-4505.

Moreno, P., Andrade, G. N., Angulo Meza, L., & Soares de Mello, J. C. C. B. (2015). Evaluation of Brazilian electricity distributors using a Network DEA model with shared inputs. IEEE Latin America Transactions, 13(7), 2209-2216.

Oliveira, E., Soares de Mello, J. C. C. B., Pereira, C. R., Machado, T. d. B., Alves, A. M., & Ramos, T. G. (2015). Assessment of sustentability on agriculture using multicriteria methods. Interciencia, 40(7), 492-496.

Pereira de Souza, M. V., Diallo, M., Castro Souza, R., & Baidya, T. K. N. (2010). The cost efficiency of the brazilian electricity distribution utilities: A comparison of bayesian SFA and DEA models. Mathematical Problems in Engineering, 2010.

Pessanha, J. F. M., Souza, R. C., & Da Costa Laurencel, L. (2007). Um modelo de análise envoltória de dados para o estabelecimento de metas de continuidade do fornecimento de energia elétrica. Pesquisa Operacional, 27(1), 51-83.

Soares de Mello, J. C. C. B., Gomes Júnior, S. F., Angulo-Meza, L., & Mourão, C. L. d. O. (2015). Condorcet method with weakly rational decision makers: A case study in the formula 1 constructors' championship. Procedia Computer Science, 55, 493-502.

Soares de Mello, J. C. C. B., Gomes, L. F. A. M., Gomes, E. G., & Soares de Mello, M. H. C. (2005). Use of ordinal multi-criteria methods in the analysis of the Formula 1 World Championship. Cadernos Ebape.BR, 3(2).

Soares de Mello, M. H. C., Quintella, H. L. M. d. M., & Soares de Mello, J. C. C. B. (2004). Avaliação do desempenho de alunos considerando classificações obtidas e opiniões dos docentes. Investigação Operacional, 24(2), 187-196.

Tschaffon, P. B., & Angulo Meza, L. (2014). Assessing the Efficiency of the Electric Energy Distribution using Data Envelopment Analysis with undesirable outputs. IEEE Latin America Transactions, 12(6), 1027-1035.

Valladares, G. S., Gomes, E. G., Soares de Mello, J. C. C. B., Pereira, M. G., dos Anjos, L. H. C., Ebeling, A. G., & Benites, V. D. (2008). Principal component analysis and ordinal multicriteria methods to study organosols and related soils. Revista Brasileira De Ciencia Do Solo, 32(1), 285-296.

1. Graduada en Engenharia de Produção pela Universidade Federal Fluminense. Atua como analista de gestão na CBO - Companhia Brasileira Off shore. bitencourt.mirley@gmail.com

2. Graduada em Pesquisa Operacional pela Universidad Nacional Mayor de San Marcos, mestrado e doutorado em Engenharia de Produção pela COPPE/UFRJ. Atualmente é professora da Universidade Federal Fluminense. lidiaangulomeza@id.uff.br

3. Graduada em Engenharia Mecânica e Mestre em Engenharia de Produção pela Universidade Federal Fluminense. Atualmente é professora da mesma universidade. mhelena@id.uff.br

4. Graduado em Engenharia Mecânica, Mestre em Matemática pela Universidade Federal Fluminense e Doutorado em Engenharia de Produção pela COPPE/UFRJ.  Atualmente é professor da Universidade Federal Fluminense. jcsmello@producao.uff.br