ISSN 0798 1015

Vol. 38 (Nº 34) Año 2017. Pág. 15

Metodología de Cálculo del Beta: Beta de los Activos, Beta Apalancado y Beta Corregido por Cash

Methodology of Calculation of the Beta: Beta of the Assets, Beta Leveled and Beta Correlated by Cash

Armando Lenin TÁMARA Ayús 1; Ignacio Emilio CHICA Arrieta 2; Aníbal MONTIEL Ensuncho 3

Recibido: 16/02/2017 • Aprobado: 02/03/2017

Contenido

1. Introducción

2. Diferentes metodologías del cálculo de la Beta

3. Conclusiones

Referencias bibliográficas

1. Introducción

El presente trabajo se realiza con el objeto de dar una visión de lo que es la beta en el modelo CAPM (Capital Asset Pricing Model) y las posibles formas para calcularlo. Para esto se parte de la definición de Sharpe (1964) que plantea que el Beta de un activo no es más que el coeficiente de volatilidad del activo, el cual nos muestra cuanto varia el rendimiento del activo en función de las variaciones del rendimiento del mercado en el cual se encuentra dicho activo. Es así como el Beta puede tomar valores mayores o menores a 1, dichos valores muestran la relación del activo con el mercado, de tal forma que:

Una Beta mayor a 1 nos indica que el activo es agresivo, es decir, una variación del mercado provoca una variación mayor a este en el activo. Lo anterior es favorable cuando el mercado está en etapa de crecimiento más no cuando está en etapa de recesión, por eso estos activos poseen un mayor riesgo sistemático.

Una Beta igual a 1 nos indica que el activo es neutral, es decir, una variación del mercado provoca la misma variación en el activo.

Una Beta menor a 1 nos indica que el activo no es agresivo, es decir, una variación del mercado provoca una variación menor a este activo. Lo anterior indica que dichos activos varían menos que el mercado en su conjunto, por eso estos activos poseen un menor riesgo sistemático.

1.1. Desarrollo del cálculo de la Beta

Para ver la utilidad del Beta es necesario referenciar el modelo CAPM, dicho modelo se utiliza para medir el costo de oportunidad del capital de un activo. El modelo está construido de la siguiente manera:

Finalmente se ha llegado a la fórmula que se utiliza para apalancar la beta del activo.

Dentro del desarrollo de las diferentes metodologías en el cálculo de la beta, se presenta a continuación las metodologías más utilizadas y una aplicación al mercado colombiano.

2.1. El Beta en el mercado

En finanzas se utilizan muchos modelos entre ellos los modelos para medir el riesgo, la Beta hace parte de uno de ellos, de este se desprenden dos características básicas que son:

1. La Beta no mide el riesgo total, solo mide el riesgo agregado a una cartera diversificada.

2. La Beta mide el riesgo relativo de un activo, ya que están estandarizados en torno a ese activo.

Para ver con claridad estas características se procede a calcular la Beta de un activo a través de una regresión lineal entre los rendimientos del activo frente a los rendimientos del mercado durante un tiempo o período razonable. Lo anterior implica que la ordenada representa el rendimiento del Activo y la abscisa el rendimiento del Mercado, por lo tanto, la ecuación de la regresión queda de la siguiente forma:

Es así como el Beta se puede encontrar de tres maneras diferentes utilizando como insumos los precios históricos de la empresa y seleccionando un índice que represente el mercado, es con base en estos como se calculan las rentabilidades discretas tanto de la empresa como del mercado, aquí se menciona paso a paso como se podría calcular o encontrar el Beta de una empresa:

1. Se descargan los precios mensuales tanto de la empresa como del índice de una fuente reconocida y aceptada, y se guardan en un archivo de Excel.
2. Se calcula la rentabilidad de la empresa y del índice de la siguiente manera:

Teniendo como base lo anterior, se puede encontrar la Beta de una empresa de tres maneras, así:

1. Se realiza en Excel un gráfico de dispersión donde la ordenada son los rendimientos de la empresa y la abscisa son los rendimientos del mercado (Ehrhardt, 1994), seguido se le solicita una línea de regresión lineal con la respectiva ecuación, donde la pendiente será el Beta de la empresa.
2. Una forma más estadística es la de Grinblatt y Titman (2002), que calculan la Beta de una empresa como:

3. Damodaran (2002) plantea en excel la utilización de la opción "Pendiente (X,Y)", donde en la "X" se debe seleccionar el vector de rentabilidades del índice y en la "Y" se debe seleccionar el vector de rentabilidades de la empresa.

Un ejemplo práctico de cómo se calcula el beta de una empresa es el siguiente: Se toma como mercado referente la Bolsa de Valores de Colombia (BVC) y dentro de ella se toma como referencia dos índices que son el IGBC (Índice General de la Bolsa de Colombia y representa el conjunto de las acciones más representativas de Colombia) y el COLCAP (es un indicador que refleja las variaciones de los precios de las 20 acciones más liquidas de la BVC, donde el valor de la Capitalización Bursátil Ajustada de cada compañía determina su nivel de ponderación).

La empresa considerada es Nutresa la cual hace parte de las empresas que se incluyen en la conformación de los dos índices referentes del mercado colombiano, el período de tiempo para el cual se estima el Beta de la compañía es de siete años el cual comprende desde enero del 2008 hasta noviembre del 2014, basándonos en Ross, Westerfield y Jaffe (2002) los rendimientos que se calcularon fueron mensuales y discretos procurando con esto tener suficientes observaciones a la hora de calcular la Beta. Para calcular la beta de esta empresa se utiliza la opción (1) presentada anteriormente, es decir, se realiza una gráfica de dispersión en Excel y se solicita una línea de tendencia con su respectiva ecuación.

Gráfica 1. Calculo del Beta de Nutresa.

Fuente: Cálculos del autor con base en datos de Bloomberg.

Como nos muestra la gráfica 1 la relación entre los rendimientos de Nutresa y el IGBC son positivos, en este caso la Beta es de 0,7372. Para realizar un mejor análisis vamos a cambiar el IGBC por el COLCAP como representación del mercado con el objeto de ver qué ocurre con el valor del Beta de la empresa.

Gráfica 2. Calculo del Beta de Nutresa.

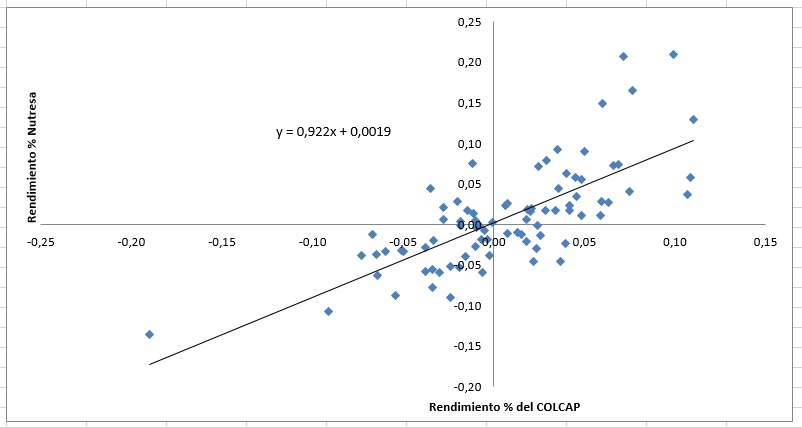
Fuente: Cálculos del autor con base en datos de Bloomberg.

Para este caso la Beta encontrado es de 0,922, es decir, en ambos casos el Beta es positivo y muy cercano a uno. A continuación, se muestra una tabla comparativa de la Beta de Nutresa con base en los dos índices del mercado de valores de Colombia y el S&P 500 (Standard and Poors), este último representa el mercado norteamericano.

Tabla 1. Cálculo del Beta de Nutresa.

Fuente: Cálculos del autor con base en datos de Bloomberg.

La pregunta a realizar sería: cuál de estos índices es el adecuado a la hora de estimar la Beta y si la elección de uno de ellos marca alguna diferencia?. La tabla 1 nos indica que para el caso de Nutresa existe una clara diferencia entre el Beta calculado con base en un índice del mercado de la bolsa de valores colombiana y la Beta calculado con base en un índice del mercado norteamericano. En primera instancia, los dos primeros Betas de la tabla establecen una relación positiva entre los rendimientos de la empresa y el mercado, mientras que el tercero nos muestra una relación negativa entre la empresa y el mercado norteamericano; en segunda instancia, los cambios que ocurran en el mercado colombiano impactan menos en la empresa dado que las Betas encontrados están muy cercanos a 1, mientras que los cambios en el mercado norteamericano tienen un mayor impacto sobre la empresa dado que su valor además de ser negativo es superior a 1. En harás de dar una respuesta de cuál se considera el mejor Beta o el Beta más acorde a la empresa, la respuesta sería un Beta de 0,922 debido a que Nutresa es una empresa colombiana lo que implica que debe referenciarse con el mercado colombiano, por otro lado, el COLCAP es el mejor indicador debido a que es un índice ponderado con base en el precio y liquidez de las empresas que lo componen.

A continuación, se muestra una tabla con las Betas de las principales empresas que componen la Bolsa de Valores de Colombia y que hacen parte tanto del IGBC como del COLCAP.

Tabla 2. Cálculos de la Beta de las empresas colombianas.

(*) El período de tiempo corresponde a 3 años y medio aproximadamente.
Fuente: Cálculos del autor con base en datos de Bloomberg.

De la tabla anterior se pueden hacer varias deducciones:

1. Nutresa, Grupo ARGOS, Cemargos, Bancolombia, Cemargos y Grupo EXITO son las empresas cuyos Betas convergen más a uno, esto puede explicarse en gran medida a la diversificación de los productos que ofrecen al mercado.

2. Empresas como Davivienda, Canacol Energy y Grupo AVAL son Betas alejados de 1 en gran medida a que son empresas cuya cotización es relativamente nueva en el mercado colombiano.

3. La empresa Ecopetrol tiene un Beta de 1,1930 y su peso en el mercado es muy representativo, de tal manera que se puede afirmar que esta es una de las empresas que jalona el índice de la BVC, ya sea el IGBC o el COLCAP.

4. Nutresa y Grupo Aval son las empresas cuyos Betas calculados con base en el mercado colombiano van en contravía al Beta calculado con base en el mercado norteamericano.

Después de haber hecho un análisis de las Betas de las principales empresas del mercado de valores de Colombia en un período de tiempo largo, se procede a realizar un análisis con base a diferentes períodos de tiempo, en este caso períodos que van desde un año hasta aproximadamente 7 años con el objeto de ver cómo ha sido la evolución del Beta para estas empresas. La siguiente tabla nos muestra los resultados de los cálculos realizados tomando como base la metodología de cálculos de Betas que hemos venido realizando.

Tabla 3. Cálculo de la Beta por períodos de las empresas colombianas.

Fuente: Cálculos del autor con base en datos de Bloomberg.

De lo anterior, podemos ver que las empresas con mayor antigüedad nos permiten tener un mejor número de datos para la estimación de la beta, pero también podríamos tener el efecto de un cambio en la beta dado los cambios en las características en términos del mix del negocio y del cambio en el apalancamiento por parte de esta. Para estas empresas en general su mix de negocios ha variado muy poco, es más, muchas de ellas han optado por especializarse en un reducido número de productos y/o servicios.

Lo anterior, no implica que siempre que se necesite la beta de una empresa este se proceda a calcularlo, Dumrauf (2010) afirma que la mayoría de veces las betas se extraen de fuentes secundarias, es decir, se utiliza una beta calculado con base en varias empresas que pertenezcan a un mismo sector y a un mismo mercado. Una de estas fuentes es la página wed http://pages.stern.nyu.edu/~adamodar/ del profesor Aswath Damodaram de la Escuela de Negocios de la universidad de New york quien realiza el cálculo de las diferentes betas, tanto para países desarrollados como para países emergentes como el nuestro.

2.2 Beta ajustado

Si se tiene en cuenta que con el tiempo las betas de las empresas tienden a uno, se hace necesario realizar un ajuste de estos, lo cual sería lógico si consideremos que las empresas que sobreviven en el mercado por lo general aumentan su tamaño a través del tiempo y son más diversificadas, a la vez que aumentan sus activos.

Cuáles empresas sus betas convergen más rápido a uno o por el contrario todas convergen con la misma rapidez?. Debe quedar claro que la convergencia de las betas son diferentes, esta depende de que tan diversificada sea la empresa, por lo tanto, las empresas con mayor diversificación su beta converge a uno con mayor rapidez frente aquellas empresas que se enfocan en un solo negocio.

(…) The bloomberg Adjusted. Bloomberg, an investiment information service, adjusts estimated betas with the folloqing formula:

The bloomberg Adjustement formula lowers betas that exceed 1 and increases betas that are under 1 (Grinblatt & Titman, 2002).

Bloomberg realiza un ajuste basado en la observación de Blume (1975) donde ve una tendencia de las betas a 1 con el pasar del tiempo:

Thus, this evidence strongly suggests that there is a substancial tendency for underlying values of beta to regress towards the mean over time (…). In other words, companies of exteme risk –either high or low- tend to have less extreme risk characteristics over time (Blume, 1975).

El ajuste de la beta que realiza bloomberg consiste en elevar los betas menores a 1 y disminuir los betas mayores a 1, la razón de lo primero es que las empresas con estos betas menores a uno poseen un bajo nivel de transacción en los mercados y es por eso que se catalogan como “pequeñas empresas”, mientras que lo segundo, empresas con betas mayores a uno son aquellas cuyas acciones en el mercado de valores se tornan atractivas para los inversionistas y, por  lo tanto, se transan más activamente, a estas empresas se les llama “Grandes empresas”.

Veamos a continuación como quedarían las betas de las empresas que se vienen trabajando:

Tabla 4. Calculo del Beta ajustado (Bloomberg) de las Empresas Colombianas.

Fuente: Cálculos del autor con base en datos de Bloomberg.

Como lo muestra la Tabla 4, el ajuste que realiza bloomberg efectivamente empuja todas las betas estimados de la regresión a uno. Hay que tener en cuenta que los pesos son los mismos para todas las empresas y no son una precisión de la estimación de la beta.

2.3 Beta ajustado por caja

Algunas empresas poseen excedentes de caja la cual no hace parte del negocio y no posee relación con la rentabilidad del mercado al cual pertenece, por otro lado, al correlacionar la caja con la rentabilidad del mercado obtendríamos una beta igual a cero, debido a que la caja no sufriría cambio alguno independiente de lo que pase en el mercado.

Lo anterior implica que cualquier empresa que posea un excedente de caja es obligación corregir su beta, esto se logra con la siguiente formula:

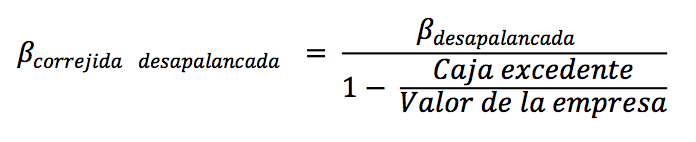
Cabe resaltar que si la empresa posee deuda se debe apalancar la beta corregida por caja con el fin de obtener el nivel de deuda correcta.

2.4. Betas contables

Este tipo de betas nos sirve para estimar los parámetros de riesgo relativo de las ganancias contables y dejar de lado el de los precios negociables, visto de otra manera, las variaciones de los ingresos en una empresa ya sean mensuales, trimestrales, semestrales o anuales pueden relacionarse frente a los cambios en las ganancias del mercado durante ese mismo período. Las betas contables son muy útiles en aquellas empresas que no poseen datos históricos del precio de su acción o por el contrario poseen demasiado ruido.

A pesar de que lo anterior suene muy atractivo, este tipo de enfoque posee tres problemas:

1. Las ganancias en las empresas tienden a ser suavizadas con respecto al valor subyacente de la empresa, lo que produce una beta sesgado hacia abajo para las empresas riesgosas y una beta sesgado hacia arriba para las empresas menos riesgosas.
2. Las empresas en su gran mayoría poseen factores no operacionales los cuales pueden influenciar las ganancias desde el punto de vista contables o pueden sufrir cambios en los métodos de depreciación entre otros.
3. El período de consolidación de las ganancias contables se realiza trimestral y/o anuales lo que implica regresiones con pocas observaciones.

Adicional a estas tres razones los mercados de países emergentes poseen limitaciones como:

• Escasa capitalización de las bolsas.
• Baja representatividad de los índices de las bolsas.
• Continuos cambios en la composición de los índices.
• Cotización intermitente de algunas empresas.
• Ausencia de datos estadísticos.
• Alta volatilidad.

Todas esas razones se convierten en argumentos para afirmar que las betas en estos mercados son inestables.

Con el objeto de comparar las betas de la regresión calculados anteriormente se procede a realizar un ejercicio de cálculo de betas contables para las mismas empresas que se vienen trabajando. Para este trabajo se tiene en cuenta el índice Colcap, los estados financieros trimestrales de las empresas, las ponderaciones de las empresas establecidas para el cálculo del Colcap según metodología de la Bolsa de Valores de Colombia.

Las betas contables que se calculan en este trabajo se obtienen comparando la medida de rendimiento contable de la compañía y la misma medida de rendimiento contable del mercado, lo anterior esta argumentado bajo el supuesto de que existe una correlación significativa con la beta de mercado, por lo tanto, al existir esta correlación la beta contable tiende hacia la verdadera beta de la empresa.

El primer paso a desarrollar para el cálculo de la beta contable es calcular el ROE (Return on equity), así:

Dentro de este paso se calcula igualmente el ROA (Return on asset), así:

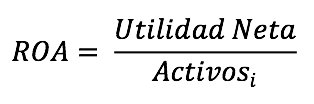
Ross, Westefield y Jaffem (1999) definen el ROE y el ROA como tasas de rendimientos contables. Para el caso que estamos desarrollando los cálculos de estos indicadores se realizaron de manera trimestres desde el primer trimestre del 2008 hasta el tercer trimestre del 2014.

A continuación, se presenta los resultados de la empresa Nutresa en cuanto al cálculo del ROA y del ROE, adicional se calcula el logaritmo natural de cada uno de estos indicadores con el fin de calcular las diferencias logarítmicas que se necesitan para el cálculo de las betas contables.

Tabla 5. Calculo del ROE y ROA de Nutresa.

Fuente: Cálculos del autor con base en datos de Bloomberg.

A continuación, se presenta los cálculos del COLCAP.ROE y COLCAP.ROA.

Tabla 6. Calculo del ROE y ROA de Nutresa.

Fuente: Cálculos del autor con base en datos de Bloomberg.

En la tabla 6 se calculó la rentabilidad del COLCAP.ROE y del COLCAP.ROA mediante diferencias logarítmicas dando como resultado retornos continuos del índice COLCAP financiero estimado, por lo tanto, dicha rentabilidad pertenece al índice del mercado.

Para calcular la beta contable se necesita los retornos continuos tanto de la empresa como del mercado los cuales ya se han calculado, por lo tanto, se puede proceder a calcular las betas a través de la siguiente formula:

A continuación, se presenta las diferentes betas calculados para las empresas en estudio:

Tabla 7. Calculo de los Betas contables.

Fuente: Cálculos del autor con base en datos de Bloomberg.

Como se puede observar existe una clara diferencia entre las betas calculados a través del ROE y las betas calculados a través del ROA, por otro lado, las empresas de energía se caracterizaron por tener betas negativas al igual que Banco Bogotá y Pacific Rubiales. Una curiosidad en el resultado de las betas es que ninguno de ellos fue superior a uno y más bien todo lo contrario, las betas se encuentran alejados de uno.

3. Conclusiones

El modelo CAPM se sigue utilizando hoy en día como un referente para el cálculo del costo del equity y es bajo este modelo donde aparece la utilización de la beta como un parámetro que sirve para estimar el riesgo.

La beta como parámetro puede tomar valores mayores o menores a uno mostrando con esto la sensibilidad que tenga la empresa frente al mercado donde se encuentre. La beta se puede calcular de varias maneras, ya sea como una relación entre los rendimientos del precio de la acción versus el rendimiento del índice del mercado o se puede plantear su cálculo de manera contable, es decir, utilizando los estados financieros de la empresa para calcular el ROE y el ROA como índices de rentabilidad de la empresa y enfrentarlos contra el índice del mercado.

No existe una verdad única o generalizada sobre cual forma es mejor a la hora de obtener la beta de una empresa, hoy en día incluso a la hora de valorar las empresas algunas valoradores optan por tomar la beta de una fuente secundaria con lo cual hacen caso omiso de los problemas que pueda tener esto.