

Vol. 38 (Nº 23) Año 2017. Pág. 4
Carlos Alberto Gonçalves da SILVA 1
Recibido: 23/11/2016 • Aprobado: 12/01/2017
4. Resultados Empíricos e Análises
RESUMO: O presente artigo examina a volatilidade dos retornos diários dos preços à vista da commodity milho por meio dos modelos de variância condicional, também chamados heteroscedásticos. A análise compreende o período de 03 de janeiro de 2006 a 29 de agosto de 2016. Os resultados empíricos demonstraram as reações de persistência e assimetria na variância dos respectivos retornos, ou seja, boas e más notícias impactam diferentemente sobre a volatilidade dos retornos de acordo com os modelos EGARCH (1,1), TARCH (1,1) e APARCH (1,1). Contudo, o modelo heteroscedástico que mais se adequou aos dados foi o EGARCH (1,1) com distribuição t student, do ponto de vista da realização de previsões. Os resultados empíricos sugerem a utilização de instrumentos estratégicos de hedge mais adequados diante da persistência acentuada de choques na volatilidade dos retornos dos preços do milho. |
ABSTRACT: The main objective of this paper was to examine the nature of the volatility of daily returns of spot prices of commodity corn. To accomplish this goal conditional variance models, also called heteroskedasticity models were used. The data employed in the analysis goes from January 3rd, 2006 to August 29rd, 2016. The empirical results showed reactions of persistency and asymmetry of their returns. In other words, good and bad news impact differently on the volatility of the daily returns according to the EGARCH (1.1), TARCH (1.1) and APARCH (1.1) models. However, from the standpoint view of performing predictions, the heteroskedasticity model that best adapted to the data was the EGARCH (1.1) with Student's t distribution. The empirical results of the analysis suggest the necessary utilization of strategic hedge instruments, given the accentuated persistency of volatility in the daily returns of corn prices. |
A cultura de milho se consolida na atualidade como a segunda maior atividade agrícola brasileira. Os dados da Companhia Nacional de Abastecimento (CONAB) demonstram que o cereal representou 41,43% de toda a produção de grãos do país na safra 2013/2014, com 80,05 milhões de toneladas produzidas.
No cenário mundial da produção agrícola, hoje o milho é o cereal mais produzido, sendo esperada 989,30 milhões de toneladas para a safra 2015/2016. A produção mundial concentra-se basicamente em três grandes produtores: EUA, China e Brasil, esses países representam 65,62% da produção mundial de milho. O Brasil se encontra na terceira posição no ranking de produtores e são aguardados 75,00 milhões de toneladas para a safra 2015/2016 de acordo com a CONAB.
No cenário brasileiro, o Estado do Mato Grosso destaca-se como um grande produtor da commodity desde a safra 2012/2013, e o município de Sorriso é considerado o maior produtor de cereal em âmbito nacional. Não obstante, das dez maiores cidades produtoras de milho no Brasil, seis se encontram em Mato Grosso.
No que tange à comercialização e consumo do milho brasileiro, grande parte da produção é direcionada às exportações. De maneira geral grande parte desse milho é destinada à produção de rações que servirão como alimento de aves e suínos nos países importadores. Os principais importadores do milho brasileiro se encontram no oriente, destacando-se: Irã, Vietnã, Coreia do Sul, Japão e Taiwan. Os mecanismos dessa comercialização se dão principalmente pelo mercado à vista conhecido como spot ou mercado futuro com a participação de intermediários financeiros, no Brasil BM&FBOVESPA e CETIP.
O preço do milho é cotado internacionalmente, e a Bolsa de Mercadorias de Chicago- CME parece como a principal referência para os preços internacionais dessa commodity. A escolha da Bolsa de Chicago como referência mundial se dá pela alta concentração da oferta e da demanda dos principais países produtores e importadores neste mercado.
A volatilidade pode ser expressa pelos movimentos oscilatórios dos preços dos produtos de commodities negociados na Bolsa de Mercadorias e Futuros, quanto mais voláteis sejam esses preços, maiores serão os riscos deste investimento. Qualquer modelo de volatilidade tem como finalidade descrever o comportamento da volatilidade passada e, através deste, prever a volatilidade futura. Uma característica importante no mercado financeiro é a existência de um comportamento assimétrico na volatilidade, ou seja, períodos de elevada volatilidade tendem a ser mais persistentes do que os períodos de baixa volatilidade.
Assim sendo, neste estudo o objetivo é avaliar empiricamente o processo de volatilidade dos retornos dos preços da commodity milho; examinando-se dois fatores determinantes, a persistência de choques e assimetrias na volatilidade, por meio da aplicação dos modelos heteroscedásticos.
Engle (1982) em seu trabalho seminal teve como objetivo estimar a variância da inflação no Reino Unido, a partir de informações e dados dos anos 70. O resultado de seu trabalho evidenciou a existência de variância condicional nessa série de retornos, projetando posteriormente uma grandiosidade de trabalhos sobre o modelo ARCH, doravante apresentado. Em sua segunda publicação, Engle se utilizou da modelagem ARCH para a definição do risco de uma carteira de investimentos, assumindo que o mesmo seguia um processo de variância condicional. Em 2001, na publicação “The use of ARCH/GARCH models in applied econometrics”, Engle, através dos modelos ARCH e GARCH comprovou que em diversas séries temporais financeiras, as várias extensões desses modelos podiam ser testadas e exibidas, como por exemplo, na precificação de ativos e análises de carteiras, revalidando e corroborando a aplicação do modelo ARCH em finanças.
A generalização do modelo ARCH foi elaborada por Bollerslev (1986) quando apresentou o modelo GARCH. Bollerslev propôs a inserção de variância de defasagens no modelo, uma espécie de instrumento adaptativo, enquanto que no modelo ARCH original, a variância condicional é função das variâncias amostrais. A apresentação empírica do modelo foi baseada na taxa de inflação americana, e logo depois disso, o modelo foi amplamente aceito e utilizado, inclusive por Engle.
Nelson (1991) estruturou a partir dos modelos ARCH/GARCH uma nova abordagem- “Conditional Heteroskedasticity in Asset Returns: A New Approach”- no qual o autor adiciona um complemento exponencial ao modelo ARCH, derivando-o ao modelo Exponencial Generalized Autoregressive Conditional Heteroscedasticity (EGARCH), reiterando ainda, perspectivas para mais pesquisas.
Zakoian (1994) considerou uma alteração no modelo clássico ARCH proposto por Engle. No seu trabalho foi apresentado o modelo TARCH, onde o desvio padrão condicional é uma função linear por partes dos valores passados do ruído branco. Esta forma específica permitiu que diferentes reações da volatilidade de sinais diferentes fossem captadas pelo modelo.
Enfim, o surgimento do modelo ARCH e suas derivações levaram à sua aplicação em diversos trabalhos, inclusive no Brasil. Mól et al. (2003) examinaram a volatilidade do retorno diário do café por meio de modelos da classe ARCH. Os resultados empíricos sugeriram fortes sinais de assimetria na volatilidade das séries mais distantes do vencimento do contrato e indicaram que todos os modelos estimados tiveram bom desempenho, e mais especificamente o modelo EGARCH, que demonstrou maior qualidade de predição no retorno do preço do café.
Martins (2005) modelou a volatilidade dos retornos diários dos contratos futuros do café arábica negociados na BMF & BOVESPA entre os anos de 1998 a 2005 com extensões do modelo ARCH. Os resultados empíricos sinalizaram a presença de assimetria a boas e más notícias e o agrupamento de volatilidade. O modelo que mostrou maior capacidade preditiva foi o TARCH. Ademais, constatou que principalmente notícias de .mudanças climáticas apresentam fortes reflexos sobre a cotação dos preços café.
Silva et al. (2005) examinaram o processo da volatilidade dos retornos de duas importantes commodities agrícolas brasileiras (café e soja), no período mensal entre 1967/2002 e 1957/2002, respectivamente, por meio de modelos ARCH. Os resultados mostraram um comportamento semelhante da volatilidade para as duas séries temporais, bem como a percepção de que um choque na variância dos preços de ambas as commodities tendiam a persistir por um longo tempo, o que por sua vez poderia culminar na elaboração de políticas públicas para a manutenção da agricultura.
Monte (2007) analisou a volatilidade nos preços do cacau cotados no Mercado de Futuros de Nova York entre os anos de 1989 e 2005 com a utilização dos modelos heteroscedásticos de variância condicional GARCH, EGARCH e TARCH, demonstrando que as constantes variações no preço do cacau foram ocasionadas, principalmente pela entrada de “boas” ou “más” notícias no mercado. Quando as “boas” notícias entravam no mercado, os agentes econômicos firmavam posições de compra no Mercado de Futuros, caso contrário, eles recuavam tomando posições avessas ao risco.
Sachs e Margarido (2007) empregaram os modelos de variância condicional para analisar a volatilidade na série de preços do boi gordo no Estado de São Paulo no período compreendido entre os anos de 2000 e 2007, utilizando-se duas variantes do modelo ARCH: os modelos, TARCH e EGARCH. Os resultados mostraram que a série de retornos do boi gordo possuía forte persistência e pouca volatilidade. Os retornos apresentaram assimetria, sendo que impactos negativos foram mais acentuados do que impactos positivos.
Campos e Campos (2007) aplicaram os modelos ARCH e GARCH para caracterizar e analisar a volatilidade das séries de retornos mensais da soja, café, milho e boi gordo. A análise empírica da volatilidade mostrou que estes produtos são marcados por acentuadas flutuações de preços, em que choques positivos ou negativos geraram impactos com longo período de duração. O somatório dos coeficientes de reação e persistência da volatilidade mostrou valores próximos ou maiores do que 1, indicando que os choques na volatilidade iriam perdurar por algum tempo na variância dos retornos dos preços das respectivas commodities.
Silva (2008) modelando a volatilidade dos retornos do preço do boi gordo no estado de São Paulo, a partir de modelos de variância condicional, apontou que no modelo GARCH, a soma persistência e reação da volatilidade do período analisado, superaram uma unidade, e que, um choque na série dos retornos do preço do boi gordo teriam efeito por muito tempo na volatilidade destes retornos, ou seja, a redução dos impactos da variância ocorreria no longo prazo. E para captar a assimetria de boas e más notícias sobre a volatilidade, foram utilizados os modelos EGARCH e TARCH, que demonstraram através de coeficientes que más notícias tendem a ter mais impacto sobre a volatilidade dos preços do boi gordo do que boas notícias.
Mól (2008) investiga o processo da volatilidade dos retornos de café arábica e boi gordo através de modelos gaussianos e assimétricos da classe ARCH. Os resultados empíricos mostram fortes sinais de persistência e assimetria na volatilidade de ambas as séries. Observou-se que os retornos de café arábica caracterizam-se por respostas assimétricas com efeito alavancagem.
Moraes e Silva (2010) utilizaram os modelos de variância constante e condicional EWMA e GARCH, respectivamente, para estimação da volatilidade dos preços do café arábica. Os resultados empíricos demonstraram que uma mesma base de dados permite resultados diferentes para estimação da volatilidade, e que tal fato impacta diretamente no apreçamento de derivativos financeiros.
Pereira et al. (2010) analisaram os retornos de três commodities importantes para o agronegócio brasileiro: soja, café e boi gordo. Foram utilizados os modelos da família ARCH e, de forma complementar, estimou-se o Value-et-Risk (VaR), compreendendo o período 30-07-1997 a 12-11-2008. Observou-se que os retornos de café e soja caracterizam-se por respostas assimétricas aos choques positivos e negativos, embora o efeito alavancagem não tenha sido identificado.
Silva e Ferreira (2013) examinaram a volatilidade dos retornos diários do preço à vista do café arábica por meio dos modelos de variância condicional, também chamados heteroscedásticos. Os resultados empíricos demonstraram as reações de persistência e assimetria na variância dos respectivos retornos, ou seja, boas e más notícias impactam diferentemente sobre a volatilidade dos retornos de acordo com os modelos EGARCH (1,1) e TARCH (1,1). Contudo, o modelo heteroscedástico que mais se adequou aos dados foi o EGARCH (1,1) com distribuição t student.
Sáfadi e Freitas (2015) analisaram a persistência, a alavancagem e a variância condicional dos retornos de commodities (etanol, açúcar, soja, milho, café, algodão, arroz, trigo, frango, boi gordo e bezerro), utilizando o modelo APARCH. Os resultados mostraram que a variância condicional foi assimétrica apenas nos retornos do etanol, do café, do algodão, do boi gordo e do bezerro.
Para testar a estacionariedade das séries, será utilizado neste trabalho, o teste ADF (Dickey – Fuller Aumentado) (1979), no sentido de verificar a existência ou não de raízes unitárias nas séries temporais. O teste de Dickey-Fuller Aumentado (ADF) consiste na estimação da seguinte equação por Mínimos Quadrados Ordinários (MQO):

O teste Phillips e Perron (PP) também é usado para investigar a presença de raiz unitária da série. O que difere entre os dois testes é o fato de que o teste Phillips-Perron garante que os resíduos são não correlacionados e possuem variância constante. Ao contrário do teste Dickey-Fuller Aumentado, o teste de Phillips-Perron não inclui termos de diferenças defasadas, mas pode também incluir termos de tendência e um intercepto.
O teste KPSS [Kwiatkowski, Phillips, Schmidt e Shin (1992)], surgiu como uma forma de complementar a análise dos testes de raiz unitária tradicional, como testes ADF e PP. Ao contrário dos testes ADF e PP, o teste KPSS, considera como hipótese nula que a série é estacionária, ou estacionária em torno de uma tendência determinística, contra a hipótese alternativa que um caminho aleatório está presente.
O teste de normalidade Jarque-Bera (JB) é baseado nas diferenças entre os coeficientes de assimetria e curtose da série e os da lei normal, servindo para testar a hipótese nula de que a amostra foi extraída de uma distribuição normal. Para a realização deste teste, calcula-se, primeiramente a assimetria e a curtose dos resíduos e utiliza-se a estatística de teste:

onde JB é o teste Jarque-Bera, S é o coeficiente de assimetria das observações, C é o coeficiente de curtose das observações e n é o número de observações. Sob a hipótese nula de normalidade, a estatística JB segue a distribuição qui-quadrado com dois graus de liberdade. Se o valor de JB for muito baixo, a hipótese nula de normalidade da distribuição dos erros aleatórios não pode ser rejeitada. Se o valor de JB for muito alto, rejeita-se a hipótese de que os resíduos ou erros aleatórios se comportam como uma distribuição normal. Se o valor p da estatística qui-quadrado calculada for suficientemente baixo, pode-se rejeitar a hipótese de que os resíduos têm distribuição normal. Se o valor p for alto, se aceita a hipótese de normalidade.

A proposição original, elaborada por Engle (1982), mereceu extensos debates e diversos aperfeiçoamentos ao longo dos anos. Bollerslev (1986) terá constatado que muitas aplicações de modelos ARCH a séries reais conduzem a valores para p muito elevados exigindo, assim, muitas restrições aos parâmetros do modelo para garantir a positividade das variâncias.

O modelo GARCH (p, q) pode ser expresso da seguinte maneira:
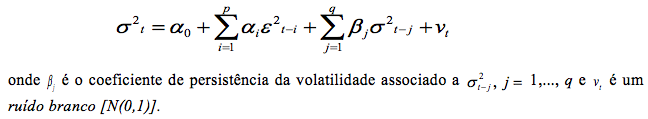
A fim de se garantir que a variância condicional não seja negativa, bem como a estacionariedade do processo, tem-se que:
![]()
O modelo GARCH (p, q) captura corretamente diversas características observadas nas séries históricas financeiras, tais como a leptocúrtica e o agrupamento de volatilidade, não captura o efeito de alavancagem, pois a variância condicional é função apenas das magnitudes das inovações e não dos seus sinais. Assim, surgiram outros modelos com a capacidade de captar a assimetria, tais como os modelos EGARCH, TARCH e APARCH.
O modelo EGARCH (Exponential Generalized Autoregressive Conditional Heteroscedasticity) proposto por Nelson (1991) consiste em captar os impactos assimétricos nas séries de dados, não tendo que exigir-se a positividade dos coeficientes.
A variância condicional do modelo EGARCH é dada por:

Um modelo mais simples, para a captação do efeito alavancagem, onde choques positivos e negativos no mercado geram impactos diferentes sobre a volatilidade nas séries financeiras, foi apresentado por Glosten, Jagannathan e Runkle (1993) e por Zakoian (1994), denominado por TARCH (Threshold ARCH). Neste modelo, a variância condicional é dada por:

Por fim tem-se o modelo ARCH com potência assimétrica (APARCH), proposto por Ding et al. (1993), o qual pode ser representado por:

Conforme apresentado anteriormente no item 3.4 , para cada modelo, serão ajustados as distribuições Gaussiana (Normal), t-Student e Generalized Error Distribuition (GED), descritas a seguir pela função log-verossimilhança.
Balakrishnan e Nevzorov (2003) mostram que a função densidade da probabilidade normal é a distribuição mais utilizada como parâmetro de comparação em aplicações estatísticas (análise de regressão, séries temporais, etc). Assim a distribuição normal é definida como:

Pode-se dizer que uma amostra obedece a uma distribuição Log-normal se os logaritmos de seus valores apresentam a uma distribuição normal, ou seja, representada pela seguinte maneira:

Hsieh (1989) e Baillie & bollerslev (1989) mostraram que a distribuição t- Student pode capturar desempenho dos log-retornos em séries temporais. Assim, a função densidade da probabilidade pode ser descrita como:

3.5.3. GED ( distribuição generalizada de erro)
A distribuição (GED) foi introduzida por Subbotin em 1923 e sendo inicialmente utilizada por Box e Tiao (1973), e posteriormente por Nelson (1991). A função densidade de probabilidade GED é expressa como:

Essa distribuição generaliza a distribuição Normal podendo ter caudas mais leves (k>2) ou mais pesadas (k<2) do que a Normal Padrão (N(0,1)) e se k=2 obtemos a distribuição Normal.
Os dados utilizados neste estudo se referem aos preços diários do milho (R$/saca de 60 kg), compreendendo o período de 03/01/2006 a 29/8/2016, num total de 2653 observações diárias. Os dados foram obtidos do site do Centro de Estudos Avançados em Economia Aplicada (CEPEA-ESALQ/USP). O software utilizado para se estimar a regressão dos dados e dos modelos de análise foi Eviews 8.0.
Os retornos diários foram calculados através da fórmula: rt=ln(Pt) - ln(Pt-1) Sendo que Pt representa o preço da commodity milho no dia t e Pt-1 o preço da commodity milho no dia anterior (t-1).
As Figuras 1 e 2 mostram o comportamento das séries de cotações dos preços e retornos diários dos preços da commodity milho no período considerado.
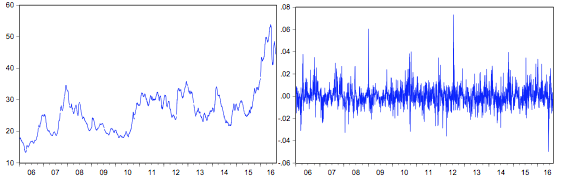
Figura 1 - Cotações diárias do preço à vista Figura 2 - Retornos diários do preço do milho.
(R$/saca de 60 kg).
Na inspeção visual da Figura 2, dentro do período de análise, nota-se uma acentuada volatilidade nos retornos, com a presença de outliers Dessa forma foi preciso testar a normalidade e estacionariedade da série dos retornos diários dos preços do milho para aplicação dos modelos heteroscedásticos.
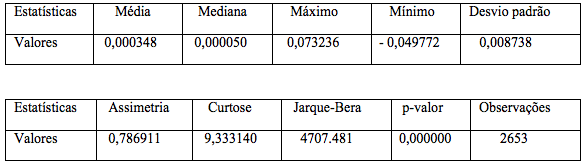
Algumas estatísticas descritivas básicas são apresentadas na Tabela 1. Observa-se que os retornos diários dos preços do milho apresentam uma distribuição leptocúrtica devido ao excesso de curtose (9,333140) em relação à distribuição normal (3,0). A estatística de Jarque-Bera indicou a rejeição da normalidade da distribuição da série, com p-valor igual a zero.
Tabela 1 – Sumário estatístico dos retornos dos preços do milho
O Q-Q Plot representa um dos métodos gráficos mais utilizados na verificação da normalidade de séries temporais. O procedimento empregado consiste na comparação gráfica dos quantis teóricos da distribuição normal com os quantis dos dados amostrais. A Figura 3 mostra a existência de uma relação não linear entre os quantis teóricos e empíricos, bastante acentuada nas caudas das distribuições, indicando caudas mais pesadas na distribuição empírica. Assim sendo, todos os testes rejeitaram a hipótese de normalidade da série analisada.

Figura 3 - Plot Q-Q Retornos diários dos preços do milho.
Antes de se efetivar a modelagem Box-Jenkins, é possível verificar formalmente se as séries dos retornos são estacionárias. Assim, os testes Dickey-Fuller Aumentado (ADF) (1979) e Phillips-Perron (PP) e (1988) e Kwiatkowski, Phillips, Schmidt e Shin (KPSS) com constante e com tendência, identificaram que as séries de retornos do milho são estacionárias e não contém raízes unitárias, conforme se observa na Tabela 2.
Tabela 2 – Teste de estacionaridade para a série dos retornos dos preços do milho.

Fonte: Elaborada pelo autor.
Após a confirmação da estacionariedade, procedeu-se a escolha dos modelos ARMA para a estimação da equação da média da série do retorno dos preços do milho, visando eliminar o problema de correlação serial. Dentre os modelos analisados foi escolhido o modelo ARMA (1,1), com base nos critérios de informação de Akaike (AIC) e Schwartz (SBC), o qual melhor se ajustou ao comportamento da série.
Antes de estimar os modelos GARCH, foi necessário realizar o teste ARCH para verificar se há ou não presença de heteroscedasticidade nos resíduos dos retornos, efetuou-se o teste LM (multiplicador de Lagrange) proposto por Engle (1982). Os valores do teste estão apresentados na Tabela 3. Observa-se que o teste mostra evidências contra a hipótese nula de não haver heteroscedasticidade condicional nos resíduos dos retornos do milho.
Tabela 3 – Teste ARCH.

Fonte: Dados da pesquisa
Assim sendo, foi modelada uma série de modelos de persistência e assimetria (família ARCH), no sentido de observar a dinâmica da volatilidade dos retornos dos preços do milho. Foram calibrados doze modelos, utilizando três tipos de distribuições para os resíduos: normal (gaussiana), t de student e GED (Generalized error distribution).
Os modelos destacados em negrito na Tabela 4 foram os que obtiveram os melhores resultados de previsão. Uma característica importante da análise é que os modelos que consideram uma distribuição condicional diferente da normal (gaussiana) apresentaram melhores resultados. A distribuição t Student obteve o melhor grau de ajuste de acordo com todos os critérios utilizados (AIC, SBC e log-verossimilhança).
Tabela 4 - Critérios de seleção entre as distribuições de erros dos modelos
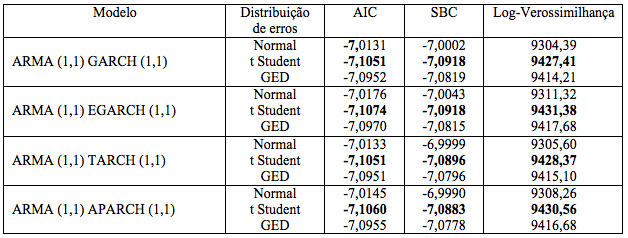
Fonte: Elaborada pelo autor.

Tabela 5 – Resultados da estimação dos modelos
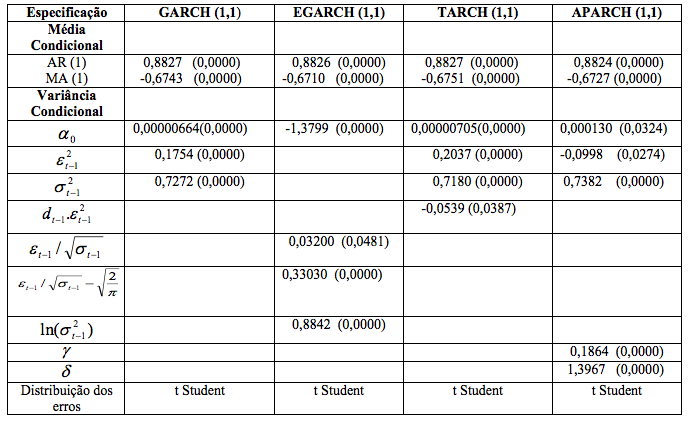
Os números entre parênteses são os valores de probabilidade (p - value), calculados ao nível de significância de 5%.
Fonte: Resultados da pesquisa. Elaborada pelo autor

A assimetria da volatilidade nos retornos do milho indica que eles oscilam em função das informações das boas e más que entram no mercado.
Já no modelo ARMA (1,1) - APARCH (1,1) - t Student, o valor positivo de 0,1864 obtido para o coeficiente (y1) significa que choques negativos passados têm um impacto mais forte na volatilidade condicional do que choques positivos passados.
Para verificar as medidas de avaliação de desempenho da capacidade preditiva dos modelos, utilizaram-se os critérios de informação de Akaike (AIC), Schwartz (SBC), log verossimilhança, erro absoluto médio (MAE), raiz do erro quadrático médio e coeficiente Theil-U. Os resultados obtidos encontram-se apresentados na Tabela 6. Assim sendo, o melhor modelo para a previsão da volatilidade dos preços do milho foi o modelo ARMA (1,1) -EGARCH (1,1) - t student. A variância dos retornos do milho brasileiro está sujeita à assimetria e não fornece evidência de alavancagem. Já em relação à persistência, o modelo escolhido resulta em um valor de 0,8842, indicando que os choques na volatilidade irão perdurar por algum tempo. Observa-se pelo coeficiente Theil-U que o modelo é aceitável, já que a estatística U é menor que um, indicando ser capaz de traçar previsões mais precisas que previsões ingênuas. Portanto, as informações no mercado são assimétricas e que notícia negativa como quebra de safra, más condições climáticas, entre outras, que acabam afetando diretamente na oferta de milho, contribuindo de forma expressiva na volatilidade dos preços do produto.
Tabela 6 – Medidas de Qualidade dos Modelos

Fonte: Resultados da Pesquisa. Elaborada pelo autor.
AIC é o critério de informação de Akaike. SBC é o critério de informação de Schwartz.
Ln (L) é a máxima log-verossimilhança do modelo estimado.
MAE é o erro absoluto médio.
REQM é a raiz do erro quadrático médio.
* denota o melhor modelo segundo o critério em questão.
O uso dos modelos heteroscedásticos foi essencial para a análise da volatilidade do preço do milho, pois de maneira genérica, pesquisas que envolvem a cadeia produtiva ainda são escassas devido à complexidade dos aspectos macroeconômicos que envolvem o tema. Os modelos utilizados apresentam fortes avanços metodológicos no tratamento dos retornos dos preços do milho, servindo como ferramentas importantes no gerenciamento de risco pelos investidores.
Os resultados empíricos mostraram reações de persistência e assimetria na volatilidade, ou seja, os choques negativos e positivos têm impactos diferenciados sobre a volatilidade dos retornos, o que pode ser comprovado pelos modelos EGARCH (1,1) e TARCH (1,1).
Com base nos critérios Akaike, Schwartz, log verossimilhança, erro absoluto médio, raiz do erro quadrático médio e coeficiente Theil-U, o modelo escolhido para a previsão da volatilidade foi o ARMA (1,1)- EGARCH (1,1)-t student. A volatilidade dos retornos dos preços do milho mostra fortes sinais de assimetria, indicando que choques negativos e positivos tem impacto diferenciado sobre a volatilidade dos retornos. Verificou-se que os choques tendem a repercutir durante algum tempo. A situação do mercado do milho apresenta a todo o momento fortes evidências comprobatórias deste resultado, uma vez que o choque de oferta cria elevações nos níveis de preços da commodity.
Os resultados empíricos sugerem a utilização de instrumentos estratégicos de hedge adequados diante da persistência acentuada de choques na volatilidade dos retornos dos preços do milho.
Baillie, R. T.; Bollerslev, T. (1989). The message in daily exchange rates: A conditional variance tale. Journal of Business and Economic Statistics, 7, 297-305.
Balakrishnan, N.; Nevzorov, V. B. (2003). A primer on statistical distribuitions. New Jersey.
Bollerslev, T. (1986). Generalized Autoregressive Condicional Heteroskedasticity. Journal of Econometrics, 31(3), 307 – 327.
Box, G. E.; Tiao, G. E. (1973). Bayesian Inference in statistical analysis. Massachussetts: Addison-Wesley, Reading.
Campos, K., C.; Campos, R., T. (2007).Volatilidade de preços de produtos agrícolas: uma análise comparativa para soja, café, milho e boi gordo. In: XLV Congresso da Sociedade Brasileira de Economia. Londrina, Paraná.
CEPEA – Centro de Estudos Avançados em Economia Aplicada. ESALQ/USP. Htpp//cepea.esalq.usp.br
CONAB- Companhia Nacional de Abastecimento. Htpp//www.conab.gov.br
Dickey, D.A.; Fuller, W.A (1979). Distribution of the estimators for autoregressive times series with unit root. Journal of the American Statistical Association, 74, 427-431.
Engle, R. F. (1982).Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50(4): 987-1007.
Glosten, L. R.; Jagannathan, R.; Runkle, D. E. (1993).On the relation between the expected value and the volatility of the nominal excess returns on stocks. Journal of Finance, 48(4), 1779-1801.
Hsieh, D. (1989). Modeling heteroskedasticity in daily foreign exchange rates. Journal of Business and Economics Statistics, 7, 307-317.
Jarque, C.; Bera, A. (1987).Test for normality of observations and regression residuals. International Statistical Review. 55(2), 163-172
Kwiatkowski, D., Phillips, P.C.B., Schmidt P.; Shin, Y. (1992) Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics, 54(1): 159-178.
Martins, C. M. F. (2005)A volatilidade nos preços futuro do café futuro brasileiro e seus principais elementos causadores. 2005. Dissertação de Mestrado em Administração - Universidade Federal de Lavras - UFLA, Lavras.
Mol, A. L. R. (2008). Séries de tempo com erros não lineares: uma avaliação da persistência e assimetria na volatilidade de derivativos de café e boi gordo na BM&F. INTERFACE, v.5, n.2, 55-69.
Mól, A. L. R.; Junior, L. G. C.; Sáfadi, T. (2003). Value at risk dos ajustes diários: o uso de modelos heteroscedásticos em futuros do café. Revista BM&F, nº 160.
Monte, L. F. O. (2007). Análise da volatilidade nos preços do cacau no mercado de futuros de Nova York (CSE): uma aplicação dos modelos GARCH, 164f. Dissertação de Mestrado em Economia, Universidade da Amazônia - UNAMA, Belém.
Moraes, L.; Silva, C. A. G. (2010). Análise da volatilidade do preço do café: uma aplicação dos modelos EWMA e GARCH. In: XVII Simpósio de Engenharia de Produção – SIMPEP 2010, Bauru.
Nelson, D. B. (1991).Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica. 59(2), 347 – 370.
Ormond, J. G. P.; Paula, S. R. L.; Filho, P. F. (1999). Café: (re) conquista dos mercados. In: BNDES Setorial, Rio de Janeiro, nº 10, p. 3-56. Disponível em: < http://www.bndes.gov.br/SiteBNDES/export/sites/default/bndes_pt/Galerias/Arquivos/conhecimento/bnset/set1001.pdf>. Acesso em 20 mar. 2011.
Pereira, V. F.; Lima, J. E.; Braga, M. J.; Mendonça, T. G. (2010). Volatilidade condicional dos retornos de commodities agropecuárias brasileiras. Revista de Economia, V. 36, n.3 (34), 73-94.
Phillips, P.C.B.; Perron, P. (1988).Testing for a unit root in time series regression. Biometrika, 75(3), 335-346.
Saith,W.; Kamitani E. L. T. (2012). Volatilidade e assimetria de choques no mercado agropecuário brasileiro um uso dos modelos da família GARCH. Tecnologia & Ciência Agropecuária. João Pessoa, v.6, n.1, p.1-7 março.
Silva, C. A. G. (2008).Análise da volatilidade do boi gordo no Estado de São Paulo: uma aplicação dos modelos GARCH. In: XLVI Congresso da Sociedade Brasileira de Economia, 2008, Rio Branco, Acre.
Silva, C. A. G.; Ferreira, L. R. (2013). Uma análise empírica da volatilidade dos preços a vista do café arábica. In: LI Congresso da Sociedade Brasileira de Economia, 2013, Belém, Pará.
Silva, W. S. S., Sáfadi, T.; Junior, L. G. C. (2005).Uma análise empírica da volatilidade do retorno de commodities agrícolas utilizando modelos ARCH: os casos do café e da soja. Revista de Economia Rural, Rio de Janeiro, 43(1), Jan-mar.
Zakoian, J. M. (1994)Threshold heteroskedasticty models. Journal of Economic Dynamics and Control, 18(6), 931-955.
1. Professor Visitante, Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, E-mail: carlos.silva@uerj.br e gon7silva@gmail.com