 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 37) Año 2016. Pág. 13
Giovanni E. REYES 1; Mayerly MEDINA García 2
Recibido: 09/07/16 • Aprobado:12/08/2016
2. Fundamentamentación conceptual
3. Aplicación en modelos de empresas de producción piscícola
4. Consideraciones finales y conclusiones
RESUMEN: Uno de los campos de aplicación de las ecuaciones diferenciales en administración de empresas y microeconomía corresponde al estudio de casos de producción en los cuales se incluye crecimiento de poblaciones. Por lo general las variaciones de población pueden adquirir formas exponenciales, es decir patrones no lineales. Con base en lo anterior, el objetivo de este estudio consiste en aplicar ecuaciones diferenciales a un problema empresarial de carácter económico-ecológico no línea, en el caso de producción de peces. Se realiza una breve introducción al estudio de funciones de producción, de las ecuaciones diferenciales, así como los tipos de solución que les son propios: (i) general; (ii) particular; y (iii) singular. |
ABSTRACT: Problems related to population growth constitute one of the most useful topics of applications of differential equations in management and microeconomics. Usually that sort of growth show exponential patterns, therefore it is linked to nonlinear models. Based on these aspects, the main aim of this study is the application of differential equations to a particular problem belonging to the field of management and ecological economics; it is the case of a growth pattern model evident in fish populations. This study contains a brief characterization of production functions, differential equations, and their levels of solution: (i) general; (ii) particular; and (iii) singular. |
Uno de los aspectos clave en administración en general y respecto a la economía de la empresa en particular, es el relacionado con la asignación de recursos. Aunque afecta de manera usual a la empresa, este rasgo tiene especial importancia para el área de producción u operaciones. En esto se debe tomar en cuenta las funciones de producción que operan en las organizaciones, así como –entre otras consideraciones- la evidencia o comportamiento de los retornos disminuyentes o incrementos decrecientes de la producción, y costos de oportunidad.
Estos aspectos cobran mucha relevancia en la esfera de operaciones o producción. Un componente vital en la gerencia de empresas, a lo que debe agregarse cuatro aspectos más: (i) mercadeo; (ii) finanzas; (iii) gestión de recursos humanos; y (iv) desarrollo organizacional.
Cuando en economía de empresa o microeconomía resolvemos problemas de producción basados en modelos polinomiales, estamos utilizando procedimientos de solución directa o comparada, en este último caso, por lo general se enfatiza el rasgo estático comparativo. Con mucho, esto se basa en que los modelos algebráicos se refieren a generalizaciones aritméticas. Con el cálculo, tanto diferencial como integral, introducimos métodos que imprimen un sentido dinámico a la solución de problemas.
Al abordar problemas no lineales basados en modelos polinómicos o bien trascendentes, estamos incorporando funciones cuyos valores pueden ser resueltos mediante ecuaciones diferenciales, en el contexto de procesos de resolución basados en sistemas de cálculo infinitesimal –diferencial o integral.
En las ecuaciones diferenciales encontramos expresiones que contienen –en lugar de variables que son numéricas- derivadas y por ello la connotación dinámica que les es propia. Además, es de puntualizar que este tipo de ecuaciones corresponden a modelos que ocurren en ámbitos que son secuenciales: generales, particulares, y singulares. Estos últimos nos proporcionan los datos directos de solución que se buscan.
La aplicación a un prototipo de problema relacionado con empresas que deben enfrentar tópicos de administración y economía ecológica es la ilustración fundamental de la aplicación de ecuaciones diferenciales que contiene este escrito. En específico, el caso de una empresas productora de peces.
En la actualidad los problemas ecológicos desde la perspectiva económica prometen un rico filón de actividad para estudio, en función de necesidades que se relacionan crecientemente con fenómenos tales como el calentamiento global, irregularidad en patrones de lluvia y sequía, y en comportamiento de poblaciones. [3]
En esta sección se discutirán los aspectos esenciales sobre funciones de producción y luego los referentes a ecuaciones diferenciales. Todo ello dentro de la integración teórica que se estimó pertinente para la aplicación de determinantes de población utilizando modelos de ecuaciones diferenciales, es decir modelos en los cuales las variables, más que referirse a números reales, se refieren a tasas de cambio o derivadas.
En lo referente a funciones de producción, es de subrayar que el campo de operaciones o producción tiene integración, básicamente, con dos dimensiones de la gerencia: (i) las columnas de funcionamiento; y (ii) los componentes de plataforma gerenciales. Entre las primeras se encuentran las llamadas áreas funcionales, tales como mercadeo, finanzas, desarrollo organizacional y gestión de recursos humanos.
Los componentes de plataforma de las organizaciones son aspectos más relacionados con funcionalidad de las empresas: planeación, organización, dotación de recursos o integración, evaluación, control o monitoreo, y procesos generales de retroalimentación a fin de detectar mecanismos correctivos (Plener, 2011; Martand, 2012; Berkel, 2010). [4]
Las funciones de producción integran en general ocho fases operacionales específicas: (i) selección de producto y diseño; (ii) selección de procesos específicos o particulares de producción; (iii) selección de la capacidad adecuada de producción; (iv) planeamiento de producción; (v) control de producción; (vi) control o monitoreo de calidad y costos; (vii) control de inventarios; y (viii) mantenimiento y reposición de máquinas (Nagare, 2007; Buzacott, 2013). [5]
En las funciones de producción un concepto esencial, generalmente presentado como parte de la escuela clásica de administración, se refiere a que el objetivo es generar el máximo de producción con la óptima combinación de insumos. Los insumos generales más utilizados son los de capital y trabajo. En la escuela más contemporánea, no sólo se trata de las utilidades, sino también del bienestar de la comunidad y de la sociedad en general, tal y como lo ha sostenido Porter (Liel, 2016; Machens, 2012; Vito, 2013; Reyes, 2006).
Como parte de la perdurabilidad de las organizaciones o empresas, se presentan mejoras en procesos administrativos y tecnológicos de producción. Entre los aspectos de tecnología se tienen productos y procedimientos que aplicados a los procesos productivos generan utilidades; es decir contribuyen a la obtención o fortalecimiento de los niveles de rentabilidad (Thompson, 2005; Plenert, 2011; Reyes, 2007).
Uno de los indicadores clave para determinar en qué punto una empresa, organización, o unidad de producción ha llegado a la situación en la cual maximiza sus recursos, es cuando el ingreso marginal iguala al costo marginal. En procesos de producción que se relacionan más con bienes de capital para la consecución de un bien o servicio, este nivel depende más de elementos tecnológicos, y de condiciones que son susceptibles de alterar o innovar por parte de la gerencia (OECD, 2012).
Sin embargo los procesos productivos pueden sustentarse con base en condiciones más bien externas, sobre las cuales existe poco, o abiertamente ningún control por parte de la dirección o gerencia. Este último es el caso de procesos de producciones agrícolas o pecuarias (Olalla, 2005; OECD, 2012; Reyes, 2012). [6]
En la agricultura, cuando se trata de abordar situaciones productivas dependiendo de crecimientos poblacionales, se deben tomar en cuenta, de manera dinámica esos crecimientos de los objetos productivos –las tasas de cambio que equivalen a la primera derivada de los fenómenos- además de los costos fijos, variables y marginales.
A eso se debe agregar el comportamiento de los ingresos, los cuales están sujetos a las variables del medio ambiente en los ecosistemas de las empresas –productos substitutivos, condiciones de ingreso de competidores, influencia de competidores ya establecidos, clientes, proveedores, acreedores y sistemas de innovación (Pimbert, 2011; Sorensen, 2008; y Makeham, 2009).
Cuando al análisis de costos se incorporan las variables del comportamiento se tienen curvas tradicionales de análisis de producto en función de insumos. Estos últimos agregándose de manera dinámica. De esa cuenta se tienen en general los siguientes postulados aplicables a la producción agrícola (Hedges, 2006):
La curva correspondiente al producto total tiende a ser ascendente, siempre que como condición indispensable, se mantenga una adición positiva en el producto marginal, o bien hasta que el comportamiento de este producto marginal llegue a cero.
La función del producto marginal se mantiene más alta que el producto medio, hasta que el primero de los mencionados comienza a decaer, es decir a entrar en una pendiente negativa.
El producto medio (PMe) continúa ascendiendo aún cuando el producto marginal comienza a decrecer; el PMe tiene su nivel más alto cuando corta a la curva del producto marginal. Esto también coincide con ser la cota que corresponde a la pendiente de mayor magnitud en el producto total.
Los comportamientos tradicionales o clásicos de las funciones de costo, ingreso y productos, se basan –como cualquier modelo que implica resultados y factores- en determinados supuestos. Lo que principalmente se deben tener en cuenta son: (i) que la cantidad del factor o insumo fijo permanece inalterada durante el período de producción; y (ii) que la cantidad del otro factor, o conjunto de factores –variables- puede ser ilimitada dentro de rangos específicos de producción (Pimbert, 2011).
Es evidente que en una producción agrícola o pecuaria que se encuentre diversificada, el administrador o gerente debe considerar la aplicación de los procesos de análisis marginal, en dos sentidos. Uno, de manera vectorial, en cada una de las líneas de producción. Dos, de manera agregada, conjunta o integral, considerando todas los tipos de procesos productivos, los ingresos que se tienen y su contribución a las utilidades como parte del sistema de administración de la empresa (Olalla, 2012).
En lo que respecta a los conceptos de ecuaciones diferenciales, uno de los primeros aspectos a recordar aquí es que no debemos confundir lo que son las ecuaciones diferenciales con las ecuaciones de diferencia. En las ecuaciones diferenciales las variables más que representar números reales o de variable compleja, representan derivadas de funciones. De allí el carácter con el cual nos permite trabajar este tipo de funciones. Constituyen por ello componentes de nivel superior en cálculo, que se abordan luego del dominio de los aspectos de cálculo diferencial e integral. [7]
Las ecuaciones de diferencia se refieren a un tipo específico de ecuaciones de recurrencia. En éstas, lo que se define es de manera reincidente, la especificación de una secuencia –tal el caso de la serie de Fibonacci, 1,1,2,3,5,8… Las relaciones de recurrencia son útiles en la caracterización de procesos complejos que tienen representaciones no lineales; son útiles en el estudio de procesos de caos, algunas de ellas incluyen la expresión de mapas logísticos, tales como los que se derivarían de la función:
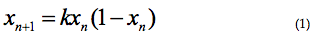
En una ecuación diferencial, una o más variables se relacionan con valores entre sí y con derivadas que pueden ser de diferentes órdenes. La aplicación de las ecuaciones diferenciales, al establecer expresiones de cambio o dinamismo en un grado más elevado que el cálculo diferencial e integral estricto, tienen amplias aplicaciones en ingeniería, física, medicina, biología en general, ecología y economía.
En muchos casos, en aquellos que presentan funciones de mayor grado de complejidad, la solución de las ecuaciones diferenciales no es directa, es decir numérica, sino que la misma es general; luego en determinadas condiciones se puede hacer particular, y con especificaciones de valores se puede tornar singular. Esta última ya tiene números directamente expresados para condiciones concretas. [8]
Las soluciones generales de las ecuaciones diferenciales tienen dos grandes énfasis de solución. En uno de ellos se aborda el análisis y soluciones de sistemas dinámicos. En el segundo gran énfasis se tienen casos de estudio basados en perspectivas estático-comparativas. En todo caso, los diferentes niveles de solución se refieren, como se ha mencionado, a generales, particulares y singulares.
Los textos dan inicio a la exposición de la teoría de ecuaciones diferenciales señalando dos grandes tipos de las mismas:
Ecuaciones diferenciales ordinarias. En este caso, la ecuación diferencial tiene una variable dependiente y una variable independiente. Tienen un orden definido que corresponde a la derivada de más alto grado que se evidencia; y
Ecuaciones diferenciales parciales. En este caso, existe una variable dependiente o endógena, y más de una variable independiente o exógena. Se utilizan aquí derivadas parciales. De manera similar a lo que ocurre con las ecuaciones diferenciales ordinarias, el orden de la ecuación diferencial corresponde a la derivada de más alto grado que se incluya. Las ecuaciones diferenciales parciales pueden involucrar tipos elípticos, parabólicos o hiperbólicos.
La aplicación que se realizará aquí corresponde a un caso de administración y economía ecológica, específicamente a los cambios que se están produciendo en una población de peces a partir de la introducción de una especie foránea. Esto implica que la población original se modifique y que se tengan que desarrollar nuevos aprovechamientos basados en la especie foránea que se está reproduciendo. [9]
El problema a resolver establece que: la población de una especie foránea está creciendo de manera exponencial, de tal forma que en un inicio se calculó una población de 50,000 peces. Cinco años más tarde la población ascendía a 75,000. Se pudo determinar que en función de “t” (t = años) el crecimiento de la especie de peces foráneos estaba dada por la función que establece tasas de variación en la dinámica poblacional.[10]
Lo que se fundamenta aquí es que la tasa de variación de una población en función de la variación del tiempo, se establece en relación con una constante de crecimiento respecto a la población. Y luego esa constante de población se relaciona con condiciones de modelo exponencial de crecimiento poblacional (el componente Poe, relacionado con la base de los logaritmos naturales y luego elevado a una constante por el tiempo (kt)).
Estamos hablando variaciones y de tendencias, es decir de tasas de cambio y no de números fijos, estáticos, no estamos hablando de números reales en directo. Esas variaciones corresponden a velocidades, se reitera: tasas de cambio, o sea se prefiere a caracterizaciones que corresponden a la primera derivada de las funciones. De allí que el modelo que se aplica a las poblaciones de peces sea una perspectiva de la población de estos, pasando así a la exposición del modelo en integrales y otros cálculos sucesivos.
Con base en lo anterior se desea determinar:
El modelo de solución general de la ecuación;
El modelo de solución particular, considerando la población de 75,000 individuos en 5 años;
La solución singular en cuanto a corroborar –con base en la solución particular- la población de 75,000 en 5 años;
La población de peces foráneos que existirá en 10 años;
El tiempo para que la población llegue a 100,000 individuos.
Solución:
Como se puede apreciar, este modelo corresponde a una ecuación diferencial ordinaria, es decir con una sola variable exógena o independiente.
Los que inicialmente se debe hacer es determinar el modelo de solución general, el cual se obtiene mediante integración:
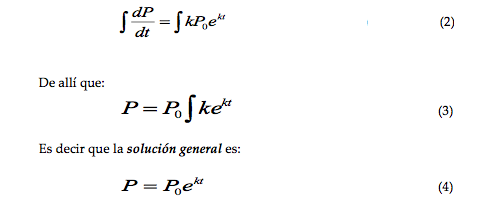
Como resultado del modelo de solución general, se tiene que P0 y k son constantes, para determinar el valor de P0 se aplica la condición inicial según la cual P = 50,000 y t = 0.

Con base en la solución particular (9) se tiene el siguiente planteamiento de solución singular:
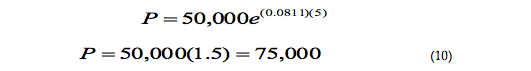
Con este cálculo la situación a 5 años está corroborada.
La solución singular se basaría en:

Por tanto, en 10 años se espera que la población de peces foráneos o introducidos, ascienda a 112,507 individuos.
Ahora la incógnita es t, por tanto se tiene:
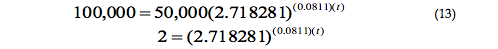
Lo que se traduce en:
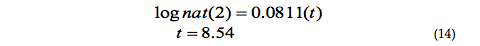
Es decir que el tiempo necesario para que la población foránea de peces alcance el número de 100,000 individuos es: de 8 años con 6 meses y aproximadamente 15 días.
En este estudio, luego de una breve caracterización de los temas de funciones de producción y de ecuaciones diferenciales, se ha procedido a ilustrar una aplicación específica a manera de modelo, sobre solución de ecuaciones diferenciales ordinarias. Se ha trabajado el nivel de soluciones generales, particulares, y soluciones particulares, dada la naturaleza de este tipo de funciones.
Con el fin de establecer la solución singular o concreta se requiere utilizar las condiciones iniciales y las llamadas condicionantes acotadas –datos específicos- respecto a las condiciones para las cuales se desea encontrar los datos de solución.
En las ecuaciones diferenciales encontramos, en función de tiempo, medidas relacionadas con razones de cambio. La solución de ecuaciones diferenciales permite tener una idea o comprensión más completa de las relaciones funcionales tomando en cuenta temporalidades y el comportamiento de las diferentes unidades de estudio en cuanto a los vectores causales que afectan.-
Basov, Suren (2007) Partial Differential Equations in Economics and Finance. (New York: Nova Science Publishers).
Berkel, Henk; et. al. (2010). Lessons from Problem Based Learning. (New York: Oxford University Press).
Budnick, Frank (2007) Matemáticas Aplicadas para Administración, Economía y Ciencias Sociales. (México, D.F.: McGraw-Hill).
Buzacott, John (2013). Production Planning and Control. (Münich: Oldenbourg).
Commom, Michael (2006) Ecological Economics: An Introduction. (New York: Cambridge University Press).
Gowdy, G. & Erickson, A. (2005). “The Approach of Ecological Economics”, en Cambridge Journal of Economics, 35, pp. 311-22.
Hammond, Peter (2008) Essential Mathematics for Economic Analysis. (New York: Oxford University Press).
Hanley, Nick; et. al. (1998) Environmental Economics in Theory and Practice. (London: MacMillan Press).
Hill, Robert; et. al. (2004) The Economics of Environment and Natural Resources. (Oxford, U.K.: Blackwell).
Liel, Benedikt (2016) Creating Shared Value as Future Factor of Competition. (Munchen, Germany: Springer).
Machens, Frank (2012) Impact of the Concept of Shared Value on Developing Countries. (Hamburg, Germany: Master Publishing).
Makeham, Joseph (2009). The Economics of Tropical Farm Management. New York: University of Cambridge Press.
Martand, Telsany (2012). Industrial Engineering and Production Management. (London: Routledge).
Nagare, Hemant (2007). Producion Planning. (Mumbai: Welingkar).
OECD (2012). Farmer Behaviour, Agricultural Management and Climate Change. Paris: OECD.
Olalla, Francisco, et.al. (2012). Agua y Agronomía. Barcelona: Mundi-Prensa.
Pimbert, Michel, et. al. (2011). Participatory Research and Farm Management. London, International Institute for Environment and Development: Russell Press.
Plenert, Gerhard (2011) International Operations Management. (Herndon, Virginia: Copenhagen Business School Press).
Reyes, Giovanni (2006) “América Latina y el Caribe: Integración e Inserción en los Mercados Internacionales” en Nómadas, Vol. 14, No. 2; 307-330.
Reyes, Giovanni (2007) “Proceso de Integración en América Latina y el Caribe: Caracterización General y Potencialidad de Nuevos Ejes de Integración” en Tendencias, Vol. 8, No. 2; 7-42.
Reyes, Giovanni (2012) “Exportaciones y Crecimiento Económico en América Latina: La Evidencia Empírica” en Comercio Exterior, Vol, 51, No. 11; 977-984, Noviembre.
Shone, Ronald (2001) An Introduction to Economic Dynamics. (Oxford, U.K.: Oxford University Press).
Sorensen, Magnus (2008). Agricultural Water Management. New York: Nova Science Publishers.
Suen, Wing (2005) The Structure of Economics: A Mathematical Analysis. (Boston: McGraw-Hill).
Thompson, George (2005) Optimal Control Theory: Applications to Management Science and Economics. (New York: Springer).
Vito, Albino (2013) Corporate Sustainability. (New York: Springer).
Zhag, Wei-Bin (2005) Differential Equations Bifurcations and Chaos in Economics. (London: World Scientific Publishing).
* Este estudio se realiza como parte de las investigaciones de la Maestría en Dirección y de la Línea de Entorno y Negocios Internacionales del Grupo de de Dirección y Gerencia de la Escuela de Administración de la Universidad Colegio Mayor Nuestra Señora del Rosario.
1. Ph.D. en Economía para el Desarrollo y Relaciones Internacionales de la Universidad de Pittsburgh, con certificados de post-grado de las Universidades de Pennsylvania y Harvard, en Estados Unidos y de la Escuela de Altos Estudios Comerciales, HEC de Paris. Es Visiting Professor de la Universidad de Maastricht en Holanda, Profesor Titular y Director del Doctorado en Ciencias de la Dirección de la Universidad Colegio Mayor Nuestra Señora del Rosario en Colombia. Email: giovanni.reyes@urosario.edu.co
2. Profesora de Carrera, Especialista en Relaciones Industriales y Gerencia de Recursos Humanos, es Directora de Bienestar Universitario y Gestión Humana en la Corporación Universitaria Minuto de Dios, UNIMINUTO, Colombia. Email: mayerly.medina@urosario.edu.co
3. Ejemplos de aplicación de modelos no lineales en: Suen, Wing (2005) The Structure of Economics: A Mathematical Analysis. (Boston: McGraw-Hill) y Thompson, George (2005) Optimal Control Theory: Applications to Management Science and Economics. (New York: Springer).
4. De conformidad con los planteamientos de Plenert (2011) y Martand (2012), se tiene una aproximación más clásica –que es la que en general se sigue en este estudio- basada en los planteamientos tradicionales de los textos de administración. En ellos, la secuencia general de los capítulos se sigue en función de componentes de plataforma administrativos –planeación, organización, integración o dotación de recursos, control, monitoreo o evaluación, además de detección de mecanismos correctivos. Los planteamientos de Berkel (2010) subrayan la importancia más didáctica en función de procesos de gestión de servicios, en especial aquellos relacionados con la prestación de servicios de salud. Véase Plenert, Gerhard (2011) International Operations Management; y Martand, Telsany (2012). Industrial Engineering and Production Management. (London: Routledge).
5. Los aportes de Nagare (2007) y Buzacott (2013) se dirigen especialmente a procesos de planeación y control con empresas que deben perdurar en ambientes de relativa inestabilidad, tales como los que se evidencian en países en desarrollo –en particular en el sur de Asia. Ambientes inestables caracterizaron a los países latinoamericanos debido principalmente a escenarios con alta inflación en los años ochenta. En algunos países como Argentina en 1989-1990 se presentaron períodos de alta inflación y alto desempleo, es decir de estanflación. Mayor discussion en Nagare, Hemant (2007). Producion Planning; y Buzacott, John (2013). Production Planning and Control.
6. Se reconoce que uno de los mayores retos de la agricultura contemporánea lo representa el conjunto de factores climáticos. Exceso o escasez de lluvia pueden rápidamente llevar a pérdidas de cosechas. Los fenómenos de El Niño, con sus temporadas cíclicas de sequía y altas temperaturas en Centroamérica y América del Sur, son ilustraciones de ese efecto en agricultura. Además, los procesos de producción vegetal y animal en términos empresariales deben enfrentar obstáculos estructurales, tales como: (i) la citada dependencia del clima; (ii) perecibilidad de productos; (iii) baja elasticidad relativa en la demanda; (iv) altas elasticidades relativas que se pueden presentar en la oferta; y (v) precios muy bajos en función de que los salarios reales de los centros urbanos se encuentran en relación directa con la capacidad de compra, especialmente de alimentos. Mayor discusión en: Olalla, Francisco, et.al. (2012). Agua y Agronomía; además del informe reciente de OECD (2012). Farmer Behaviour, Agricultural Management and Climate Change; Gowdy, G. & Erickson, A. (2005). “The Approach of Ecological Economics”; Pimbert, Michel (2011). Participatory Research and Farm Management; Sorensen, Magnus (2008). Agricultural Water Management; y Makeham, Joseph (2009). The Economics of Tropical Farm Management.
7. Una mayor discusión especialmente respecto a ecuaciones diferenciales ordinarias, en: Basov, Suren (2007) Partial Differential Equations in Economics and Finance. (New York: Nova Science Publishers); Budnick, Frank (2007) Matemáticas Aplicadas para Administración, Economía y Ciencias Sociales. (México, D.F.: McGraw-Hill); Hammond, Peter (2008) Essential Mathematics for Economic Analysis. (New York: Oxford University Press); Shone, Ronald (2001) An Introduction to Economic Dynamics. (Oxford, U.K.: Oxford University Press).
8. Véase además: Suen, Wing (2005) The Structure of Economics: A Mathematical Analysis. (Boston: McGraw-Hill); Thompson, George (2005) Optimal Control Theory: Applications to Management Science and Economics. (New York: Springer) y Zhag, Wei-Bin (2005) Differential Equations Bifurcations and Chaos in Economics. (London: World Scientific Publishing).
9. Mayor discusión de este caso en: Budnick, Frank (2007) Matemáticas Aplicadas para Administración, Economía y Ciencias Sociales. (México, D.F.: McGraw-Hill) págs: 898-903.
10. Aplicaciones más generales y discusión de casos más específicos, en la relación entre economía y ecología en: Commom, Michael (2006) Ecological Economics: An Introduction. (New York: Cambridge University Press); Hanley, Nick; et. al. (1998) Environmental Economics in Theory and Practice. (London: MacMillan Press) y en Hill, Robert; et. al. (2004) The Economics of Environment and Natural Resources. (Oxford, U.K.: Blackwell).