HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 30) Año 2016. Pág. 23

Análise do índice aluno equivalente graduação por meio da Análise Multivariada

Analysis of the equivalent undergraduate student index by means of Multivariate Analysis

Adriano Mendonça SOUZA 1; Angela Pellegrin ANSUJ 2; Jean Cauê HUPPES 3

Recibido: 25/05/16 • Aprobado: 21/06/2016

Conteúdo

1. Introdução

2. Análise multivariada

3. Cursos e variáveis analisadas

4. Resultados e discussões

5. Conclusão

Referências

1. Introdução

Nos últimos anos, a procura por ensino superior gratuito e o número de instituições tem aumentado, porém os recursos públicos destinados a este fim são escassos e insuficientes para atender a toda esta demanda (SANTOS, 2013).  Assim, vários estudos têm sido desenvolvidos com o objetivo de encontrar uma melhor forma de alocação de recursos públicos nas Instituições de Ensino Superior como Leite (2011), Santos (2013), Ferreira (2013),  Neves (2013), Bezzerra (2014), Caliman (2014), Groschupf (2015), Torres (2015).

A secretaria de Educação Superior do MEC, adota uma Matriz de Alocação de Recursos Orçamentários para as despesas de custeio e investimento das Instituições Federais de Ensino Superior – IFES, a qual é composta de diversos indicadores calculados sobre uma base de dados anuais, as quais são fornecidas pelas IFES. E um dos principais indicadores da matriz é o denominado Índice Aluno Equivalente (Nfte). A coleta e a verificação dos dados constituem-se em importantes etapas, que além de promover interação entre as IFES e destas com a SESu/MEC, constituem um Banco de Dados Acadêmicos fundamental para o desenvolvimento de estudos e análise sobre o Sistema Federal de Ensino Superior. 

O índice aluno equivalente (Nfte) é o principal indicador utilizado para fins de análise dos custos de manutenção das IFES, referentes ao orçamento de custeio e capital (OCC). O cálculo deste índice para cada instituição é formado por quatro indicadores parciais, ou seja, aluno equivalente de graduação (Nfte(G)), aluno equivalente de mestrado stricto sensu (Nfte(M),) aluno equivalente de doutorado (Nfte(D)) e aluno equivalente de residência médica (Nfte(R)). Incluem-se no cálculo todos os cursos de caráter permanente, e que não sejam auto financiados, mantidos por recursos especiais de convênios ou parcerias com instituições públicas ou privadas (BRASIL, 2005).

Neste estudo será considerado apenas o índice aluno equivalente de graduação (Nfte(G)), que é formado pelas variáveis: Duração média dos cursos (D), número de diplomados (Ndi), número de matriculados (Ni), peso do grupo (PG), fator de retenção (R), bônus por turno (BT) e bônus fora de sede (BFS).

Assim, o objetivo da pesquisa é encontrar as variáveis de maior impacto na formação do índice Nfte(G), da Universidade Federal de Santa Maria (UFSM), por meio de técnicas multivariadas. O desenvolvimento desta pesquisa é de suma importância, para identificar como os gestores dos cursos de graduação consideram as variáveis que possuem pouca participação na composição do índice.  Desta forma, é possível que cursos com poucos recursos orientem suas estratégias de gestão para as variáveis identificadas, e melhorem seu desempenho financeiro em relação a outros cursos da UFSM.

A pesquisa delimita-se apenas à Universidade Federal de Santa Maria (UFSM), envolvendo 52 cursos, dos 8 Centros de Ensino, que atendem aos requisitos do índice  aluno equivalente graduação (Nfte(G)), no ano de 2013.

2. Análise multivariada

Os métodos multivariados são apropriados quando as variáveis relacionam-se entre si, estabelecendo uma estrutura de dependência. Essa característica é que diferencia a técnica multivariada da univariada, onde cada variável é considerada individualmente, sem atenção aos inter-relacionamentos (MARDIA, 1972).

Pode-se afirmar que a análise multivariada é a área da análise estatística que se preocupa com as relações entre as variáveis, e que apresenta duas características principais: os valores das diferentes variáveis devem ser obtidos sobre os mesmos indivíduos, e que as mesmas devem ser interdependentes e consideradas simultaneamente (KENDALL, 1957). A seguir, serão descritos os métodos de análise multivariada, ou seja, análise de cluster e análise fatorial, que serão utilizados para o desenvolvimento deste estudo.

A análise de cluster, também chamada de análise de conglomerados é uma técnica usada para classificar objetos ou casos em grupos relativamente homogêneos entre si, mas diferentes entre outros conglomerados.

Os processos de aglomeração podem ser hierárquicos ou não hierárquicos. Na aglomeração hierárquica é estabelecida uma ordem, ou estrutura em forma de árvore, que produz seqüência de partições em classes cada vez mais vastas. O que não ocorre na aglomeração não-hierárquica, na qual se produz, diretamente, uma partição em um número fixo de classes (CORRAR, 2007).

Para proceder esta classificação, faz-se necessário definir matematicamente o que venha ser caracterizado proximidade, ou seja, à distância entre dois objetos, definindo-se a partir daí o critério de agrupamento de duas classes. Entre as medidas mais usuais, para estabelecer o conceito de distância entre dois objetos m e n baseada nos valores de i variáveis pode-se destacar as seguintes formas de mensuração: Coeficiente Correlação Linear de Pearson; Distância Euclidiana; Distância de Manhattan; Distância de Mahalanobis e ; Distância de Chebychev.

Após determinar o tipo de distância a ser utilizada, é preciso definir os métodos de ligação, dentro os mais usuais: método de ligação simples; método do vizinho mais distante;  método de Ward e;  método do centróide.

Nesse tipo de análise, toda a distância entre os objetos dentro de um espaço é calculada e agrupada conforme a proximidade entre eles, constituindo-se num grupo de dois objetos mais próximos. A seguir, verifica-se qual objeto se localiza mais próximo desse primeiro grupo, construindo-se um novo grupo e, assim, sucessivamente, até que todos os objetos sejam reunidos no grupo total de todos os objetos estudados.

Uma vez que os objetos encontram-se ligados por ordem de proximidade, isto é, pela menor distância, é necessário definir, igualmente, a noção de distância entre os grupos de objetos, ou particularmente, entre um objeto e um grupo.

Determinar o número de grupos a ser formados, baseando-se em estudos anteriores ou utilizando o gráfico Amalgmation linkage, busca-se compreender o porquê determinadas variáveis ou objetos pertencem a um cluster ou não, isto tudo deve ser realizado por meio de um pacote estatístico (MINGOTE, 2007).

Geralmente as variáveis são agrupadas de acordo com a correlação existente entre elas, e o resultado obtido é mostrado através do dendrograma, onde se pode verificar os clusters formados e a partir deles retirar as conclusões fornecidas pelos dados coletados. Quando se opta por uma análise de cluster, busca-se identificar variáveis homogêneas dentro do cluster e variáveis heterogêneas fora deles.

A Análise Fatorial teve seus primeiros trabalhos relatados por Charles Spearman e Karl Pearson. Segundo Spearman (1904), testou a hipótese de que diferentes testes de habilidade mental – habilidades em matemática, raciocínio lógico, verbais, entre outras – poderiam ser explicadas por um fator comum de inteligência que ele denominou “g”.  Outros autores deram continuidade a esses trabalhos como, Trurstone (1931) que desenvolveu a ideia de multiple factor analysis. Outras contribuições significativas podem ser dadas a Hotelling ao propor “o método de componentes principais que permite o cálculo da única matriz de fatores ortogonais” (KAPLUNOVSKY, 2016).

Segundo Hair et al. (2009), fator é a combinação linear das variáveis originais. A análise fatorial avalia a correlação existente entre um grande número de variáveis e identifica a possibilidade de essas variáveis serem agrupadas em um número menor de variáveis latentes e de que, obviamente, se possa identificar o significado dos agrupamentos realizados. É o mesmo que dizer que a análise fatorial avalia a possibilidade de agrupar i variáveis (X1, X2, X3, ..., Xi) em um número menor de j fatores ( F1, F2, F3...Fj).

Segundo Lírio e Souza (2004), a análise fatorial não se refere a apenas uma técnica estatística, mas em uma variedade de técnicas para tornar os dados observados mais facilmente interpretados, ou seja, analisam-se os inter-relacionamentos entre as variáveis para que possam ser descritas,  através de um grupo de variáveis originais ponderadas pelos respectivos fatores, extraídos muitas vezes por meio da técnica de análise de componentes principais, por gerarem fatores independentes.

A análise fatorial busca tornar os dados observados mais facilmente interpretados por meio dos inter-relacionamentos entre as variáveis.

De acordo com Lírio e Souza (2008), as variáveis originais podem ser escritas como uma combinação linear dos fatores, mais o termo residual que representa a dependência de uma variável em relação às demais, sendo que tais variáveis podem ser expostas  algebricamente como pode ser vista na equação (1): 

Para Malhotra (1999), a análise fatorial segue os seguintes passos: 1º) Formulação do problema; 2º) Construção da matriz de correlação; 3º) Determinação dos autovalores e autovetores; 4º) Rotação dos fatores; 5º) Interpretação dos fatores; 6º) Cálculo dos escores fatoriais e seleção das variáveis substitutas; 7º) Determinação do ajuste do modelo.

Para a realização da análise fatorial, conforme Vicini (2005), é necessário que as variáveis sejam interligadas, o que pode ser comprovado pela correlação significativa entre as variáveis e pelo teste de Kaiser Meyer Olkin (PEREIRA, 2001).

Como o propósito da AF é descrever o conjunto de dados com poucos constructos representativos, muitas vezes para uma melhor interpretação dos fatores é necessário realizar uma rotação de eixos na massa de dados. A rotação não compromete o nível de explicação dos fatores sobre as variáveis e facilita a construção de cada fator, servindo, portanto, como artifício de análise, sem influir na comunalidade.

Ao rotar os fatores, deveria fazer com que cada fator tivesse cargas, ou coeficientes não nulos, para apenas algumas variáveis, e que cada variável tivesse carregamentos não-zero, ou significativos, com uns poucos fatores, se possível com apenas um, sendo que a variância explicada pelos fatores individuais é redistribuída por rotação. As rotações mais utilizadas são: Ortogonal, Varimax e Varimax Normalizada, para maiores detalhes ver (JOHNSON e WICHERN, 1992).

3. Cursos e variáveis analisadas

O estudo envolveu os 52 cursos de graduação, nos 8 Centro de Ensino da Universidade Federal de Santa Maria, que se enquadram no índice aluno equivalente de graduação Nfte(G), no ano 2013. Os dados foram obtidos junto ao Centro de Processamento de Dados (CPD) da UFSM. Os cursos analisados foram: Agronomia (A), Administração Diurno (AD), Administração Noturno (NA), Arquivologia (AR), Arquitetura (ART), Artes Visuais - Bacharelado em Desenho e Plástica (AVB), Artes Visuais Licenciatura (AVL), Computação(C), Ciências Biológicas (CB), Ciências Contábeis Diurno (CCD), Ciências Contábeis Noturno (CCN), Ciências Econômicas Noturno (CEN), Comunicação Social - Habilitação Publicidade e Propaganda (CPP), Comunicação Social - Habilitação Relações Públicas (CRP), Ciências Sociais Bacharelado (CSB), Direito Diurno (DD), Desenho Industrial - Projeto de Produto (DIP), Desenho Industrial - Programação Visual (DIV); Direito Noturno (DN), Enfermagem (E), Engenharia Civil (EC), Engenharia Elétrica (EE), Educação Especial (EES), Educação Física Bacharelado (EFB), Educação Física Licenciatura (EFL), Engenharia Mecânica (EM), Engenharia Química (EQ), Farmácia (F), Física Bacharelado (FB), Fisioterapia (FI), Filosofia (FL), História Licenciatura/Bacharelado (H), Física Licenciatura Noturno (FLN), Fonoaudiologia (FO), Geografia Bacharelado (GB), Geografia Licenciatura (GL), Letras (Licenciatura) - Português e Literaturas de Língua Espanhola (LE), Letras (Licenciatura) - Português e Literaturas de Língua Inglesa (LI), Letras (Licenciatura) - Português e Literaturas de Língua Portuguesa (LPL), Medicina (M), Meteorologia (ME), Matemática Núcleo Comum (MLB), Matemática Licenciatura Diurno (MLD), Odontologia (O), Psicologia (P), Ciências Econômicas Diurno (CED), Pedagogia Diurno (PD), Pedagogia Noturno (PN), Química Bacharelado (QB), Química Industrial (QI), Química Licenciatura (QL), Zootecnia (Z).

3.1 Etapas metodológicas

Ao iniciar o estudo, após a coleta e a organização dos dados, antes da  utilização da análise multivariada, realizou-se a análise descritiva afim de  possibilitar o conhecimento das variáveis e auxiliar na interpretação da análise de cluster e da análise fatorial.

O método multivariado aplicado nessa pesquisa será o da classificação hierárquica, onde os objetos são agrupados à semelhança de uma classificação taxonômica e representada em um gráfico com uma estrutura em árvore, denominada dendrograma.

Para a formação dos clusters a métrica utilizada será a da distância Euclidiana que é a medida mais usual em técnica de análise de cluster. Ela pode ser calculada com base na raiz quadrada da soma dos quadrados das diferenças dos valores de cada variável analisada.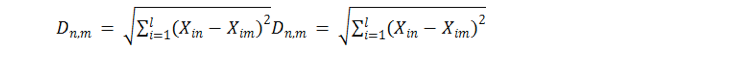         (3)

A equação (3) fornece a proximidade geométrica entre as variáveis ou objetos, e o método de aglomeração fornece de como serão agrupados os elementos, nesta pesquisa será utilizado o método do vizinho mais próximo.

A Análise de Cluster possibilitará apenas identificar as variáveis próximas e homogêneas dentro do cluster com as variáveis discrepantes e heterogêneas entre eles. A próxima etapa é a utilização da Análise fatorial, a qual fornecerá os pesos que cada variável estudada fornecerá por meio das combinações lineares encontradas, escritas por meio dos fatores loadings e das variáveis originais.

O método para determinar os fatores será o método de componentes principais, por fornecerem fatores independentes um dos outros e com solução única. Caso haja necessidade de realizar rotações para facilitar a interpretação dos fatores, será utilizada a rotação Varimax Normalizada.

Os fatores selecionados para o estudo serão aqueles que apresentarem autovalor superior a 1 ou uma variância explicada acumulada acima de 70%, desta forma procura-se realizar uma redução de dimensionalidade e identificar qual fator é mais representativo de cada etapa do processo de distribuição de recursos. Também se busca identificar quais variáveis são mais representativas em cada etapa de modo que o gestor possa utilizar esta informação para aumentar a sua participação nos recursos distribuídos entre os cursos na instituição.

4. Resultados e discussões

Nesta etapa realizou-se a análise estatística descritiva univariada e posteriormente a multivariada com o intuito de determinar hipóteses sobre o estudo que está realizado. Também se busca compreender como os 52 cursos estudados se comportam quando analisados simultaneamente em relação as 7 variáveis que compreendem o índice Nfte(G) na UFSM.

Para a identificação das variáveis mais importantes do modelo e das variáveis menos representativas, foi realizado a análise descritiva dos dados como apresentado na Tabela 1.

Tabela1 – Estatística descritiva dos 52 cursos referente às variáveis que formam o Nfte(G)

Fonte: CPD, UFSM. Elaboração do autor.

Na Tabela 1, observa-se que as variáveis Ndi, Ni e PG apresentam um coeficiente de variação extremamente alto, 83,54 e 59,21 e 51,55% respectivamente, sinalizando desta maneira que os dados apresentados no ano de 2013 não são representativos, para se utilizar a média dos indicadores tornando-se necessário a utilização da estatística multivariada como forma de alocação dos recursos financeiros. A variável BFS não apresenta variabilidade entre os cursos analisados por isso ela não será inserida nas análises multivariadas subsequentes, já que é um valor constante. As variáveis que apresentam uma variabilidade baixa são BT e D com valores do coeficiente de variação de 2,97 e 13,74%. Na Figura 1, apresenta-se o Box-Plot das variáveis, que corrobora o que foi discutido da Tabela 1.

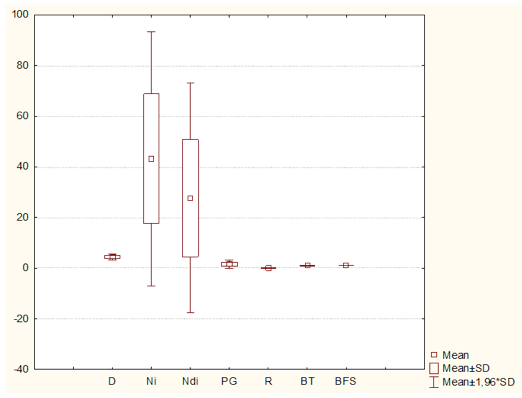
Figura 1 – Box-Plot das variáveis D, Ni, Ndi, PG, R BT e BFS dos 52 cursos da UFSM, no ano de 2013.

Na Figura 1, observa-se que as variáveis Ni (número de ingressantes) e Ndi (número de diplomados) apresentam grande variabilidade, refletindo o desacordo entre os cursos em relação a estas variáveis. Porém, não se visualiza na Figura 1, nenhum ponto discrepante entre as variáveis, mostrando que no ano analisado todas as variáveis apresentam comportamento semelhante. Ainda, com o intuito de verificar as proximidades entre as variáveis, utiliza-se a técnica multivariada de análise de cluster. Na Tabela 2, apresenta-se a distância euclidiana e a ligação simples com os dados normalizados.

Tabela 2- Matriz de distância das 6 variáveis com dados padronizados dos 52 cursos

Fonte: CPD, UFSM. Elaboração do autor.

Observa-se que as menores distâncias euclidianas entre uma variável e outra, estão localizadas entre as variáveis Ndi e Ni que corresponde a 2,2. As variáveis que apresentam maior distância euclidiana entre si são as variáveis Ni e R que corresponde a 13,4.

O resumo de todas as distâncias e das ligações finais entre as variáveis está representado na Figura 2 que, utiliza-se o “amalgmation graph” para indicar a que altura de ligação um corte deve ser realizado para determinar o número de cluster, justificando-se assim um corte na distância de ligação igual a 5, determinando 3 clusters.

Figura 2 – Gráfico para a determinação da altura em que o corte
deve ser feito no dendrograma para indicar o número de clusters

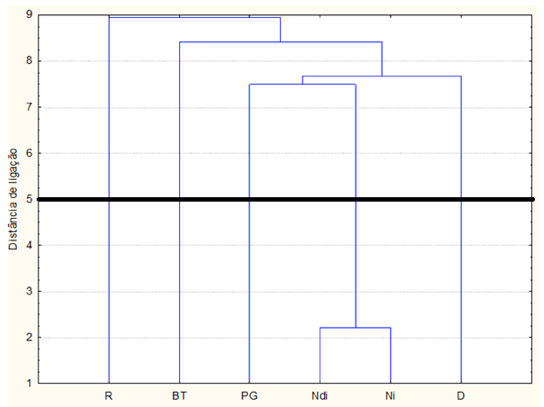
Figura 3 – Dendrograma das 6 variáveis que formam o
índice Nfte(G)  dos 52 cursos de graduação da UFSM

Na Figura 3, as variáveis que não apresentaram variabilidade foram excluídas, ou seja, as variáveis com coeficiente de variação igual à zero, pois não apresentam nenhuma variabilidade. A variável R é a mais diferente em relação ás demais variáveis, pois apresenta uma ligação com uma distância euclidiana de valor 9. A variável BT também aparece como a segunda variável mais discrepante das demais em um único cluster, já as variáveis PG, Ndi, Ni e D são similares. As variáveis Ndi e Ni são as variáveis mais similares, pois apresentam uma menor distância de ligação das distâncias calculadas no grupo.

Desta forma, visualizam-se 3 clusters distintos, Cluster 1 formado pela variável R, cluster 2 formada pela variável BT e o terceiro formado pelas variáveis PG, Ndi, Ni e D. Vale lembrar que estes clusters devem apresentar uma grande similaridade interna e uma dissimilaridade externa, mas não refletem o grau de importância destas variáveis na formação do Nfte.

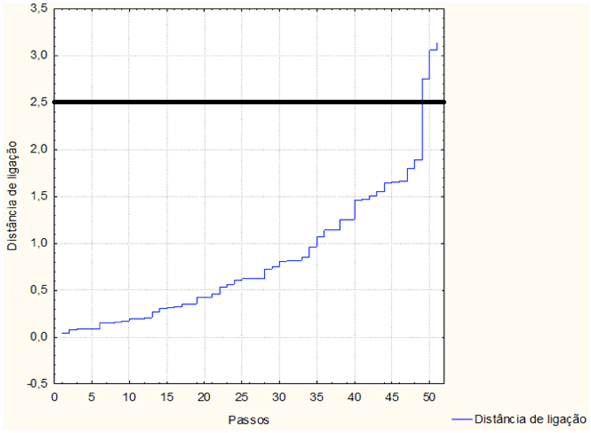
Figura 4 - Gráfico para a determinação da altura em que o corte
deve ser feito no dendrograma para indicar o número de clusters

Observando-se a Figura 4, verifica-se que na distância de ligação 2,5 é a maior distância de ligação e desta forma na metade deste valor é que se deve fazer um corte na horizontal do dendrograma para definir o número de grupos a serem formados, os quais são mostrados na Figura 5.

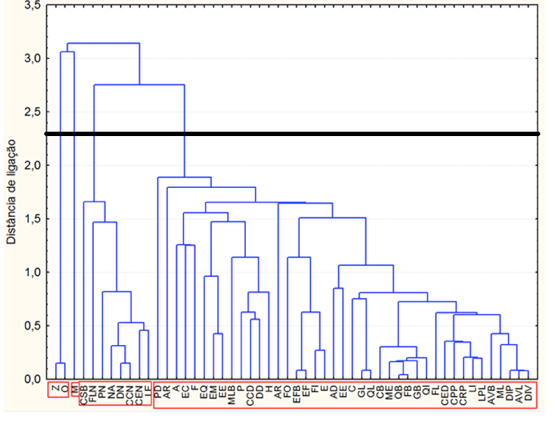
Figura 5 – Dendrograma dos 52 cursos da UFSM no ano de 2013
utilizando a métrica da distância euclidiana e método de ligação simples

Observa-se na Figura 5, a formação de 4 grupos distintos que devem ser examinados cuidadosamente. O curso mais discrepante dos demais são: Zootecnia (Z), Odontologia (O) e  Medicina (M). Os cursos mais similares são Química Bacharelado (QB) e Física Bacharelado (FB). Outrossim, não deve-se afirmar que (Z), (O) e (M), são os cursos mais relevantes, mas apenas dizer que são os cursos de se diferenciam dos demais. O curso de maior participação no índice Nfte(G) é o Curso de Medicina seguido do Curso de Odontologia. Os que apresentam menores participações na distribuição são: Música Licenciatura (ML) seguido pelo curso de Matemática Núcleo Comum (MLB).

Para determinar o peso que cada variável possui na formação do Nfte(G), utiliza-se a análise fatorial, pois desta forma é possível determinar o impacto das variáveis na formação do Nfte(G) e seu comportamento em relação os cursos. O primeiro passo a ser realizado é a determinação dos autovalores e a seleção dos mesmos, para que se realize a análise fatorial.

Tabela 3 – Autovalores e percentual de variância explicada das variáveis que compõem o Nfte(G).

  Fonte: CPD, UFSM. Elaboração do autor.

A seleção do número de fatores a ser utilizado será dada por aqueles que possuem autovalores superiores a 1 e que acumulem uma variância explicada de no mínimo 70%. Como mostra a Tabela 3,  dois fatores são selecionados com  autovalores superiores a 1, que são 3,18 e 1,3 respectivamente e que acumulam uma variância de explicação de 74,86%. Sendo suficiente 2 fatores para representar os 52 cursos em relação as 6 variáveis estudadas.

Determinado os autovalores realiza-se a extração dos fatores utilizando-se os dados padronizados de forma que uma variável não interfira nas demais, os quais estão representados na Tabela 4.

Tabela 4 - Dados padronizados na análise fatorial sem rotação

Fonte: CPD, UFSM. Elaboração do autor.

 Na extração dos fatores foram utilizadas apenas as variáveis que apresentavam variabilidade, portanto, restaram 6 variáveis e as mesmas foram padronizadas.  Da Tabela 1, vê-se que Ni e Ndi são as variáveis mais representativas seguidas por R que representam o Fator 1. Como estas variáveis representam número de ingressantes, número de diplomados e retenção, optou-se por denominá-la de Fluxo nos Cursos. Observa-se que a retenção está no eixo X no sentido positivo e Ni e Ndi em sentidos opostos. Desta forma sugere-se que os cursos apresentam maior retenção (R) do que ingressantes e diplomados. Só por esta análise justifica-se uma rotação do eixos para uma melhor interpretação.

No fator 2, a variável de maior impacto é o bônus por turno e desta forma optou-se por denominar este fator de Turno, esta variável impacta positivamente a formação do índice de distribuição de recursos Nfte(G).

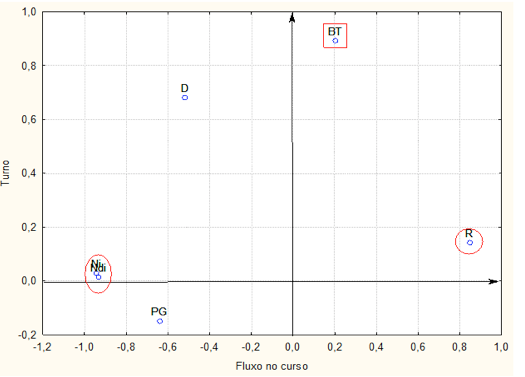
Figura 6 – Representação dos dois fatores selecionados e não rotacionados
dos 52 cursos da UFSM em relação a seis variáveis que compõem o Nfte(G)

Com o intuito de manter o mesmo grau de informação e verificar um comportamento mais claro das variáveis realizou-e uma rotação Varimax Normalizada que está representada na Figura 7.

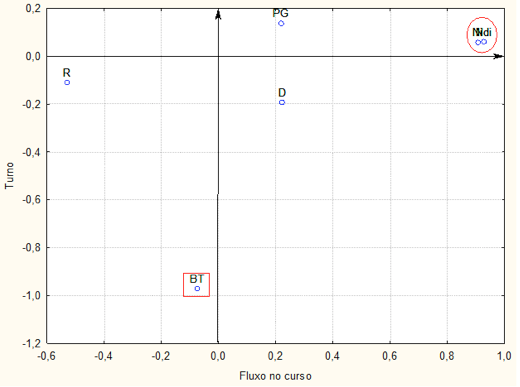
Figura 7 - Representação dos dois fatores selecionados com rotação Varimax Normalizada
rotacionados dos 52 cursos da UFSM em relação a seis variáveis que compõem o Nfte(G).

Observa-se na Figura 7, que no eixo representativo do Fluxo do curso as variáveis Ndi e Ni são as de maior ponderação estando no eixo positivo do eixo X e a variável R conta negativamente no fluxo do curso, como era de se esperar. A retenção no curso é aquela variável que faz com que o aluno não avance o fluxo normal do curso e causa problemas na liberação de vagas, no número de formandos e represa o número de vagas no curso.

No eixo Y que corresponde ao turno, a variável de maior peso é o Bônus por Curso que influencia negativamente, estando na parte negativa do eixo Y, mas se contraposto pelo peso do grupo. Duas das sete variáveis que compõem o Índice Aluno Equivalente de Graduação-Nfte(G) são informadas pela Instituição – IFES. As demais variáveis são fixadas pela Matriz Andifes, portanto, pode-se afirmar que são variáveis que o gestor administrativo das IFES não podem alterar. As variáveis alteradas são as variáveis de maior impacto na elaboração do Nfte(G).

Com o intuito de identificar as variáveis mais relevantes na formação do índice NFTe, mostra-se na Figura 10 o círculo de correlação unitário, no qual se vê que as variáveis de maior correlação são Ndi, Ni e BT, por serem as varáveis mais distantes do centro do circulo unitário e consequentemente mais próximas de 1. As demais variáveis possuem um correlação menor, mas mesmo assim são importantes.

Também é possível verificar que as variáveis que possuem um ângulo entre elas inferior a 45estão fortemente correlacionadas, como por exemplo as variáveis Ndi e Ni estão fortemente correlacionadas e são bem significativas, pois estão próximas do círculo unitário e de bastante influência no Nfte(G). Já as variáveis PG e R que estão a um ângulo de quase 1800 0 estão em sentidos opostos, o que significa que a medida que uma aumenta a outra teoricamente deve diminuir. Estas oposições é que devem ser compensadas ou trabalhadas pelos gestores de modo a permitir um melhor desempenho no índice, dado que são variáveis de intervenção governamental.

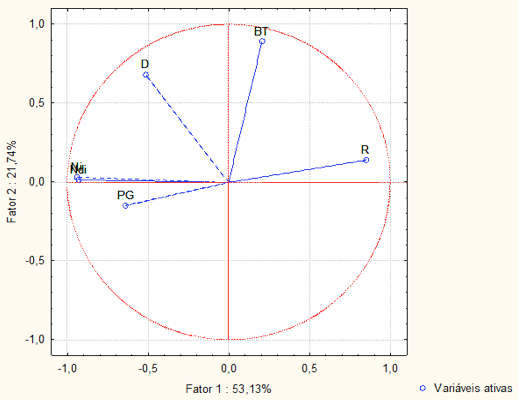
Figura 8– Círculo de correlação unitário das seis variáveis que compõem o índice Nfte(G).

Com o propósito de identificar quais os cursos estão ligados a quais variáveis, basta sobrepor o gráfico do círculo unitário sobre o plano fatorial dos cursos, mostrados na Figura 9.

Figura 9- Plano fatorial dos cursos dos 52 cursos de graduação da UFSM

Sobrepondo as Figuras 8 e 9 é possível ver quais variáveis estão ligadas a quais cursos. Por exemplo, o curso de Medicina (M), Odontologia (O), fisioterapia (F) e Engenharia Civil (EC) que estão no segundo quadrante, onde estão localizados as variáveis Ndi, Ni e D.Que representam cursos com excelente captação decursos dentro da instituição em relação aos demais cursos e é o que está ligado ao Ndi e Ni altos. O restante dos cursos apresentam uma análise análoga.

Os cursos de Ciências Sociais Bacharelado (CSB), Matemática Núcleo Comum (MLB) e Física Licenciatura Noturno (FLN), por exemplo, estão no primeiro quadrante observados na Figura 9. Ao observar a Figura 8, pode-se constatar que estes cursos, CSB, MLB e FLN estão no mesmo quadrante das variáveis BT e R.

5. Conclusão

A técnica aplicada mostrou-se capaz de identificar assertivamente as variáveis de maior impacto na formação do Nfte(G), para o caso da Universidade Federal de Santa Maria (UFSM), apontando quais as variáveis que os gestores deverão trabalhar de modo a alcançar maior participação na distribuição dos recursos financeiros.

As variáveis Ndi e Ni, devem ser sempre trabalhadas de modo a manter um alto fluxo de alunos, com baixa repetência, baixas retenções e com altos índices de diplomados. As demais variáveis que compõem o índice, são de cunho governamental. Com a identificação das variáveis mais relevantes no cálculo do índice de alocação, cabe aos gestores das  IFES adotar medidas para o escalonamento da distribuição interna de recursos financeiros. 

Conseguiu-se identificar os cursos tem maior Ndi e Ni que são os cursos de Medicina (M), Odontologia (O) e Zootecnia (Z). Outrossim, conseguiu-se identificar os cursos com menor Ndi e Ni, que são os cursos de  Ciências Sociais Bacharelado (CSB), Matemática Núcleo Comum (MLB) e Física Licenciatura Noturno (FLN).

As outras variáveis R, PG, D, BFS e BT são variáveis que os gestores ainda não possuem autonomia para gerenciar pois são fixadas pelo SESu/MEC.

Sugere-se que seja realizada uma análise para classificar e identificar os cursos com baixa, média e alta participação no Nfte(G), na UFSM, de modo que os gestores possam antecipadamente tomar medidas para melhorar o desempenho dos cursos que possuem baixo desempenho na alocação dos recursos financeiros.

Referências

BEZERRA, A.M.L. Relação entre fontes alternativas de recursos e eficiência das unidades acadêmicas na UNB. Disseração, UNB, 2014.

BRASIL. Ministério da Educação. Secretaria de Educação Superior. Cálculo do aluno equivalente para fins de análise de custos de manutenção das IFES. Brasília, 2005. Disponível em: <http://portal.mec.gov.br/calculo-aluno-equivalente-orcamento>. Acesso em: 10 de mar. 2016.

CALIMAN, D.R. Fatores que inibem a institucionalização: O orçamento como ferramenta de controle gerencial em uma IFES. Disseração, UFES, 2014.

DICKEN, P. Mudança global: mapeando as novas fronteiras da economia mundial. Porto Alegre: Bookman, 2010.

FERREIRA, S. C. Financiamento público das instituições federais de ensino superior: Uma visão do grau de engessamento dos orçamentos das universidades federais. UNB, 2013.

GROSCHUPF, S.L.B. O orçamento público como instrumento para o planejamento e desenvolvimento institucional (PDI): Um estudo de multicaso nas instituições de ensino superior públicas federais do estado do Paraná. Disseração, UTFP, 2015.

HAIR, J. F., et al. Análise multivariada de dados. Trad. Adonai S. Sant’Anna e Anselmo C. Neto. 6 ed. Porto Alegre: Bookman, 2009.

KENDALL, M.G. A course in multivariate analysis. London: Griffin, 1957.

LEITE, E. S. Reconversão de habitus: O advento do ideário de investimento no Brasil. Tese, UFSCarlos, 2011.

LÍRIO, G.S.W; SOUZA, A. M. Métodos multivariados: Uma metodologia para avaliar a satisfação dos clientes da RBS-TV na região noroeste do RS. Dissertação (Engenharia de Produção) – Universidade Federal de Santa Maria. 2004.

LÍRIO, G.S.W., SOUZA, A. M. A satisfação dos serviços pós-venda de clientes de um veículo de comunicação escrita, sob a ótica da Análise Multivariada. Ciência e Natura, UFSM, 30 (2): 21 - 41, 2008.

MALHOTRA, N. K. Pesquisa de marketing: uma orientação aplicada. Porto Alegre: Bookman, 1999.

MARDIA, K.V. Statistics of Directional Data. Academic Press, 1972.

MINGOTTI, S.A. Análise de dados através de método de estatística multivariada – Uma abordagem aplicada. BH: Editora UFMG, 2007.

NEVES, T.J.G. Um estudo de variáveis que impactam a execução física e orçamentária dos programas das universidades brasileiras. Dissertação, UFB, 2013.

PEREIRA, J.C.R. Análise de Dados Qualitativos: Estratégias metodológicas para as ciências da saúde, humanas e sociais. 2. Ed. ; São Paulo: USP, 1999.

SANTOS, F. S. Financiamento público das Instituições Federais de Ensino Superior – IFES: Um estudo da Universidade de Brasília. Dissertação, UNB, 2013.

SPEARMAN, C. General intelligence objectivelly determined and measured. American Journal of Psychology 15, p. 201-293, 1904.

TORRES, I.S. Aplicação da Metodologia BPM em uma IFES: Proposição de um Modelo Estendido. Dissertação, UFRGS, 2015.

THURSTONE, Louis L. Multiple factor analysis. Psychological Review 38, p. 406-427, 1931.

KAPLUNOVSKY, A.S. Why using factor analysis? (dedicated to the centenary of factor analysis). [online] Disponível em: <http://www.magniel.com?fa/kaplunovsky.pdf >Acesso em: 16 fev. 2016.

1. UFSM, Brasil. amsouza.sm@gmail.com
2. UFSM, Brasil. angelaansuj@yahoo.com
3. UFSM, Brasil. jeancaue@gmail.com