HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 10) Año 2016. Pág. 20

O uso da tecnologia CAE através da técnica do método dos elementos finitos no processo de desenvolvimento de válvulas de esfera flutuante

The use of CAE technology through finite element method technique in floating ball valve development process

Diego Rizzotto ROSSETTO 1; Thomas G. R. CLARKE 2; Marcos Alexandre LUCIANO 3

Recibido: 08/12/15 • Aprobado: 14/01/2016

Contenido

1. Introdução

2. Materiais e métodos

3. Condições de contorno e carregamentos

4. Critério de análise

5. Incertezas de medição

6. Modelo de elementos finitos

7. Ensaios de extensometria

8. Medição das deformações com strain gages

9. Resultados

10. Discussão dos resultados

11. Conclusão

Referências bibliográficas

1. Introdução

Segundo Mathias (2008), a válvula de esfera flutuante é um modelo de válvula muito empregado em tubulações para interromper ou permitir a passagem de fluidos. É uma válvula de movimento rotativo, na qual o obturador é uma esfera que descreve um movimento rotacional de 0º a 90º em relação ao sentido de escoamento do fluxo na tubulação, para abrir ou fechar.

Entre os maiores usuários de válvulas estão às indústrias dos setores de óleo & gás, química e petroquímica, devido à complexidade da operação possuem seus próprios requisitos de homologação de projetos. Válvulas para operação em atividade submarina é um exemplo de aplicação em situação extrema, na qual requisitos como manutenção e/ou substituição podem ser atividades de elevado custo e perigosas.

O baixo desempenho ou falha de válvulas em operação pode trazer graves consequências, tais como, perdas de produção, catástrofes ambientais e até mesmo perdas de vidas humanas, resultando com isso em severas consequências econômicas e judiciais aos operadores e fabricantes destes produtos.

Segundo CORT (1994 apud Euthymíou, 2013), as causas de falhas em equipamentos de petróleo podem ser classificadas como: (i) Defeitos de Fabricação, quando o equipamento foi fabricado ou reparado num nível de qualidade que não está de acordo com as especificações de fabricação/projeto; (ii) Defeitos de Projeto, quando o projeto não é adequado com as premissas e condições reais de operação e/ou ambientais (externas e/ou internas); (iii) Defeitos de Informação, quando há informação inadequada ou falta de informação que leve o equipamento a ser instalado, operado ou sofrer manutenção de forma incompatível com a especificação original do fabricante.

O diagnóstico do Prominp (2009 apud Weiss e Lima, 2010), indicou uma grande variedade de problemas de qualidade nos fabricantes nacionais de válvulas, no que tange: (i) Engenharia de projetos, falta de projetos estruturados de engenharia de produtos; (ii) Qualidade dos Materiais, porosidade nos materiais dos principais componentes (corpo/tampa) da válvula; (iii) Infraestrutura de testes, insuficiência de número de bancadas de teste de produtos; (iv) Engenharia de manufatura, baixa capacidade instalada de máquinas operatrizes.

Nos últimos anos, foi desenvolvida a norma ABNT NBR15827 [2], que teve seu lançamento no ano de 2007. A mesma estabeleceu critérios rigorosos para a certificação de fornecedores de válvulas do mercado nacional. Os fabricantes apoiaram o desenvolvimento dessa norma, pois entenderam que seria uma proteção do mercado nacional contra fornecedores de baixa qualificação técnica.

Neste período a norma NBR 15827 (2014) passou por diversas melhorias, sendo que a evolução ocorreu com base em pesquisas e desenvolvimentos realizados devido ao interesse de alguns fornecedores em parceria com a principal empresa petroleira do mercado nacional. Mesmo com esta evolução para muitos fornecedores o atendimento da norma acaba sendo inviável tanto pelo alto custo envolvido no desenvolvimento quanto pela falta de conhecimento técnico disponível.

Segundo estudo do Prominp (2009 apud Weiss e Lima, 2010), a realização de análise de tensões e deformações de componentes críticos por modelos de elementos finitos é um dos principais problemas enfrentados atualmente pelos fabricantes nacionais de válvulas para adequação do produto a norma NBR15827 (2014). A mesma exige que o projeto de válvulas comprove a realização de análise de tensões e deformações de componentes críticos por cálculos analíticos e/ou modelos de elementos finitos.

Segundo Biasi (2013), mesmo as maiores fabricantes de válvulas industriais do Brasil possuem dificuldades em garantir a qualidade do produto já na área de projeto, sem que haja retrabalhos no processo de fabricação dos produtos. Se o projeto da válvula não estiver robusto, as chances de o produto ser reprovado nos testes aumentam, podendo gerar retrabalho que acaba onerando o custo final do produto, diminuindo assim a competitividade do produto frente aos concorrentes.

O uso da ferramenta CAE no segmento produtor de válvulas evitaria que correções de problemas técnicos e revisões de projeto ocorram por improvisação, além de permitir o desenvolvimento de um produto de alta qualidade, desempenho e confiabilidade (Weiss e Lima, 2010).

Nakamura et. al. (2014), cita o sistema CAE (Computer Aided Engineering ou Engenharia Auxiliada por Computador), como uma importante ferramenta para a viabilização de um projeto de produto em tempo reduzido, oferecendo oportunidade para simulação e redução dos custos na fase de desenvolvimento do produto.

O sistema CAE é uma ferramenta que analisa e processa cálculo de forma a minimizar esforços braçais do engenheiro, se preocupando menos com a parte operacional e mais com a questão estratégica, fazendo do CAE uma ferramenta poderosa para redução de custos de um projeto e minimizando o tempo para o lançamento do produto (Sales, Nobre Filho e Santos, 2013).

No Brasil o processo de homologação de válvulas é regulamentado pela norma ABNT NBR 15827 (2014) e Portaria INMETRO Nº 272 (2011) no que tange a requisitos de projeto e ensaio de protótipo.

Pelo fato do teste experimental conter etapas de difícil reprodução, implicando em alto custo de infraestrutura e elevado tempo de execução, em muitos casos a execução do teste experimental acaba sendo inviabilizado.

O método de elementos finitos (MEF) consiste em uma poderosa ferramenta para análise dos diversos fenômenos físicos envolvidos em válvulas para aplicações industriais, evitando desta forma, que erros sejam detectados durante o teste de fábrica ou na própria operação e que alterações de projeto ocorram por tentativa e erro. O uso correto do MEF durante as etapas iniciais do processo de desenvolvimento de produto permite a obtenção de soluções rápidas, seguras e econômicas.

Segundo Filho (2006), no dia-a-dia das atividades de engenharia, os engenheiros e projetistas são colocados diante de problemas técnicos, alguns mais simples e outros mais complexos, tendo que resolvê-los de forma satisfatória. No desenvolvimento de cálculo de estrutural, o sucesso não está apenas condicionado ao conhecimento de um aparato matemático muitas vezes complicado, mas à capacidade que o engenheiro apresenta de entender a natureza física que se propõe a resolver (Filho, 2006).

Segundo Cook et. al. (2002), modelo matemático é uma idealização na qual geometria, propriedades de materiais, carregamentos e/ou condições de contorno são simplificadas baseadas no conhecimento do analista em entender quais aspectos são importantes ou não para obtenção dos resultados requeridos.

Elementos finitos é um método para solução numérica de problemas de campo. O modelo matemático é discretizado pela malha de elementos finitos, assim um campo contínuo é representado por pequenos segmentos, denominado elementos, que são conectados por um por um número finito de nós (Cook, 2002).

Este artigo tem como finalidade apresentar a importância do uso da tecnologia CAE durante das fases iniciais do processo de desenvolvimento de válvulas com o intuito de evitar que as correções de problemas técnicos sejam detectadas no cliente final e que possíveis correções de problemas técnicos ocorram por improvisações. Incialmente são apresentados conceitos sobre a importância da tecnologia CAE através da técnica dos elementos finitos e o atual cenário do mercado brasileiro de válvulas no que tange a engenharia de projeto de válvulas. Na sequência é elaborado um modelo mediante cinco etapas principais, que aborda todos os aspectos envolvidos numa análise numérica e experimental de válvulas. Por fim, é ilustrado um exemplo dos resultados obtidos, bem como os fatores que influenciam nos resultados entre o método numérico e experimental.

1.1 Processo de Desenvolvimento de Válvulas

Segundo Rozenfeld, et. al. (2006), de modo geral desenvolver produtos consiste em um conjunto de atividades por meio das quais se busca, a partir das necessidades do mercado e das possibilidades e restrições tecnológicas, e considerando as estratégias competitivas e de produto da empresa, checar as especificações de projeto de um produto e de seu processo de produção, para que a manufatura seja capaz de produzi-lo.

Segundo Wütemberg, et. al. (2011), a qualidade pode ser definida pelo seu preço, pela taxa de falhas, por características de uso e pela qualidade intrínseca percebida pelo cliente. A qualidade do produto é consequência direta do seu processo de desenvolvimento de produto (PDP), ou seja, dos processos, pessoas e tecnologias adotadas (Morgan e Liker, 2006).

Para que exista inovação é necessário dominar de forma criativa, diversas competências na área da engenharia e da tecnologia, possuindo uma eficaz percepção das necessidades e requisitos do mercado (Sales, Nobre Filho e Santos, 2013).

Com a introdução da Norma ABNT NBR 15827 a partir de 2007, o mercado de válvulas vem apresentando nos últimos uma significativa modernização para aumentar seu nível de competitividade.

Para atingir os níveis de exigência atual é necessário um conhecimento cada vez mais profundo sobre o comportamento do produto de acordo com a sua aplicação. Ao mesmo tempo, o ciclo de desenvolvimento de produto esta cada vez menor, tanto em termos de tempo como de investimentos.

Para aumentar a agilidade no desenvolvimento de válvulas, as empresa adotam uma série ferramentas a fim de tornar mais eficiente esta etapa sem comprometer o desempenho do produto final. O desenvolvimento a partir da realização de cálculos analíticos, simulações computacionais e testes de protótipos são alguns exemplos de etapas adotadas pelas empresas para atender os padrões de qualidade exigidos atualmente.

A análise estrutural é o tipo de simulação mais disseminada em válvulas, e visam verificar o comportamento e a integridade estrutural de componentes e do conjunto do produto de acordo com os carregamentos que representam as condições de montagem, teste de fabricação, teste de homologação e operação.

O ensaio de protótipos com a utilização de strain gage tem como finalidade a validação das simulações computacionais. Este tipo de ensaio consiste em comparar os resultados da simulação numéricos com os resultados experimentais, permitindo com isso o ajuste do modelo computacional a fim de obter maior precisão na simulação computacional.

2. Materiais e métodos

O estudo foi desenvolvido em uma válvula de esfera do tipo flutuante bipartida de bitola 3", componentes corpo e tampa obtidos pelo processo de microfusão e fabricados em aço ASTM A216 Gr. WCB, haste laminada em material ASTM A479 Gr. 410. A pressão máxima de trabalho é de 5,1 MPa, torque de acionamento de 182Nm e temperatura de ensaio de 25ºC.  Na Tabela 1, são apresentadas as propriedades físicas e mecânicas dos principais componentes da válvula analisados no estudo.

Tabela 1 – Propriedades mecânicas e físicas dos principais componentes da válvula.

O estudo numérico e experimental da válvula foi desenvolvido mediante cinco etapas: (i) Determinação das condições de contorno e carregamentos; (ii) Determinação dos critérios de análise; (iii) Determinação das incertezas de medição; (iv) Simulação numérica pelo método dos elementos finitos no programa Ansys Workbench; (v) Ensaio do modelo físico com extensômetros.

3. Condições de contorno e carregamentos

Os ensaios numéricos e com extensômetros foram realizados com a válvula na posição aberta com pressão interna no lado do corpo (Hipótese A) e posição aberta sem pressão interna com aplicação do torque de acionamento na haste (Hipótese B).

As simulações e ensaios realizados visam contemplar as mesmas características, desta forma, as simulações foram divididas em dois load cases, conforme descrito na Tabela 2.

Tabela 2 – Condições de carregamento dos ensaios numéricos e experimentais.

A hipótese A, visa simular no primeiro load case a condição de montagem da válvula e no segundo load case a condição de operação com pressão interna. Na hipótese B, o primeiro load case simula a condição de montagem da válvula e o segundo load case a condição de abertura da válvula quando a mesma não esta submetida à pressão interna.

4. Critério de análise

A extensometria é uma técnica utilizada para a análise experimental de tensões e deformações em estruturas mecânicas. O strain gage é o transdutor utilizado para medir deformações.

Engenharia Auxiliada por Computador (CAE) é uma tecnologia que utiliza o computador para dar suporte a engenharia de produto durante as fases iniciais do processo de desenvolvimento do projeto de produto. Esta técnica permite que protótipos virtuais sejam avaliados dentro de certas condições de operação. O uso da tecnologia CAE com técnicas de elementos finitos permite avaliar o estado de tensões e deformações de componentes críticos de válvulas.

A análise comparativa dos resultados das simulações numéricas com os resultados experimentais foi realizada em termos de tensões e deformações equivalentes "von Misses".

A Teoria de energia de distorção máxima ou critério de von Misses é usada para prever a tensão de falha de um material dúctil, conforme equação 1.

5. Incertezas de medição

Segundo o Guia da Incerteza de Medição, a definição do termo "incerteza de medição" é relatada como um parâmetro, associado ao resultado de uma medição, que caracteriza a dispersão dos valores que podem ser razoavelmente atribuídos ao mensurando (Bell, 1999).

Ao realizar uma medição, muitas podem ser as variáveis que dispersam os resultados. As falhas de medição podem ser visíveis ou invisíveis durante a operação. As condições de ensaio dificilmente estarão em perfeitas condições (Bell, 1999).

As componentes de incerteza são: Incerteza Herdada da Calibração, resolução dos instrumentos, variações ambientais, variável geométrica, variação das propriedades do material, método de colagem dos strain gages.

6. Modelo de elementos finitos

As análises do estudo numérico são do tipo linear, tanto para condições de contato como em termos de propriedades mecânica dos materiais. A malha gerada contém elementos tetraédricos e hexaédricos. Nos componentes de maior interesse da análise, bem como nas regiões de maior concentração de tensões foram realizados refinamentos na malha. A configuração final resultou em uma malha com um total de 705.362 nós e 197.622 elementos. A Figura 1, ilustra a malha gerada no conjunto.

Figura 1 – Malha gerada no conjunto da válvula.

7. Ensaios de extensometria

Para o ensaio de extensometria foram utilizados os seguintes equipamentos: Bomba hidropneumática, sistema de aquisição de dados, software de aquisição de dados, torquímetro, strain gages.

8. Medição das deformações com strain gages

As deformações foram avaliadas em dois pontos no componente corpo (P1 e P2) e em um ponto no componente haste (P3), conforme ilustrado na Figura 2.

Figura 2 – Regiões da válvula instrumentada com strain gages.

Como a superfície do corpo onde foi colado o extensômetro está submetido a um estado biaxial de tensões, ocorre uma superposição entre as deformações longitudinais e transversais, desta forma, utilizou-se strain gage do tipo bidirecional. Segundo Hoffmann (1989), para este tipo de extensômetro as tensões principais podem ser obtidas através das seguintes equações.

Onde:

σ1,2: Tensões principais no ponto onde foi colado o extensômetro [MPa];

E: Módulo de elasticidade do material do corpo [MPa];

ν: Coeficiente de Poisson do material do corpo;

ε1,2: Deformações medidas pelo strain gage [mm/mm].

A haste estará submetida a um estado biaxial de tensões e a tensão principal normal ocorrerá num ângulo de ±45º.  Desta forma, a medição de deformações da haste foi realizada com strain gage do tipo espinha de peixe, configurado em um circuito do tipo meia ponte.

Segundo Hoffmann (1989), para um circuito do tipo meia ponte, as tensões principais em um eixo sujeito à torção podem ser obtidas pela seguinte equação.

Onde:

σ1,2: Tensões principais na haste [MPa];

E: Módulo de elasticidade do material da haste [MPa];

ν: Coeficiente de Poisson do material da haste;

εi: Deformação resultante [mm/mm].

A deformação em um extensômetro configurado em meia ponte é obtida por:

Onde:

εi: Deformação resultante [μmm/mm];

ε1,2: Deformações principais [μmm/mm];

ε: Deformação medida pelo strain gage [mm/mm].

9. Resultados

Nesta seção são apresentados os resultados obtidos pelo método numérico. Na Figura 3, são ilustradas as deformações e as tensões equivalentes no componente corpo (P1 e P2) e no componente haste (P3) da válvula, na região onde foram colados os strain gages no modelo físico.

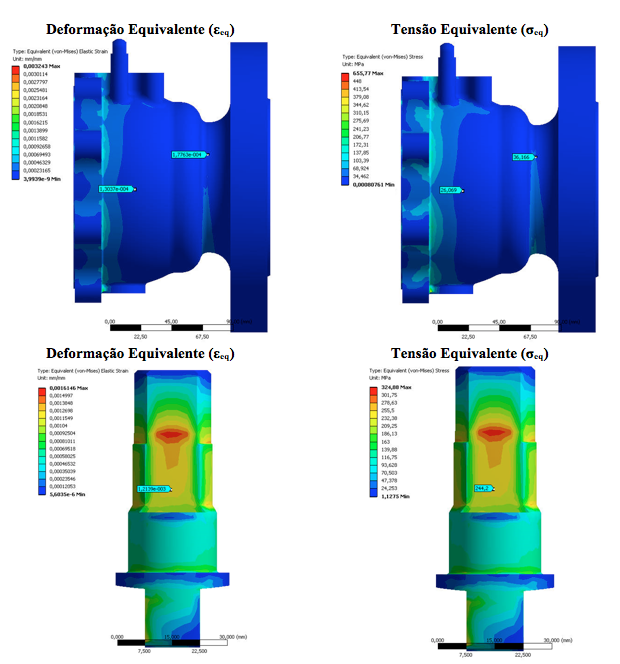
Figura 3 – Resultados das deformações e tensões equivalentes ponto 1, 2 e 3obtido por FEA.

Conforme ilustrado na Figura 3, verificou-se que o valor da deformação equivalente é em torno de 1,30x10-4 mm/mm no Ponto 1, de 1,77x10-4 mm/mm no Ponto 2 e 1,21x10-3 mm/mm no Ponto 3.  O valor de tensão equivalente ficou em torno de 26,06 MPa no Ponto 1, de 36,16 MPa no Ponto 2 e 244,2 MPa no Ponto 3.

10. Discussão dos resultados

Na Tabela 3, são apresentados os valores de deformações e tensões equivalentes obtidos pelo método dos elementos finitos e os valores obtidos pelo ensaio com extensômetros. Os valores apresentado do ensaio experimental com protótipo físico através de strain gages levam em consideração a incerteza calculada do experimento. A incerteza calculada do experimento foi de ±11,27x10-6 mm/mm, assim são apresentados o valor nominal e o valor de limite inferior e superior de deformação e tensão equivalente do ensaio. Também é apresentada a diferença percentual de tensões equivalentes em relação ao valor nominal.

  Tabela 3 – Análise comparativa dos valores de deformações principais.

Através dos resultados apresentados na Tabela 3, verificou-se que os resultados obtidos nas simulações computacionais pelo método dos elementos finitos foram próximos aos resultados experimentais, estando os valores deformações equivalentes (εeq) e tensões equivalentes (σeq) dentro da faixa de incerteza dos ensaios com extensômetros. A maior variação de deformação equivalente ocorreu no ponto 1, e a menor variação ocorreu no ponto 2. Em termos de tensão equivalente a maior variação ocorreu no ponto 1, e a menor variação no ponto 3.

As pequenas diferenças encontradas se devem principalmente à variação dimensional dos componentes, tensões internas que são geradas no processo de fabricação, presença de poros e impurezas dos componentes da válvula e que não são considerados no modelo de análise numérica, aplicação dos carregamentos, colagem dos strain gages, discretização da malha de elementos finitos.

Com relação à variação dimensional dos componentes como causadora de diferença entre resultados experimentais e numéricos se deve ao fato que as simulações numéricas são realizadas com os componentes nas dimensões nominais, entretanto, os componentes da válvula utilizada no ensaio experimental apresenta dimensões entre as margens de tolerância máxima e mínima do processo de manufatura.

No modelo numérico o material é considerado homogêneo isento de poros, impurezas e sem tensões residuais gerados pelo processo de fabricação, porém nos componentes reais da válvula há presença de impurezas, poros e tensões residuais e isso contribui para a existência dessa variação entre os resultados da análise numérica e experimental.

A colagem dos extensômetros, por sua vez, pode ocasionar grandes diferenças entre os resultados experimentais e numéricos, visto que, o posicionamento destes elementos pode não coincidir exatamente com os pontos determinados no software de elementos finitos.

11. Conclusão

O uso da tecnologia CAE pelo método dos elementos finitos se mostrou adequada para análise de válvulas de esfera flutuante, permitindo assim determinar as deformações e tensões resultantes em função dos diversos carregamentos que a válvula será submetida ao longo do seu ciclo de vida, cargas oriundas das etapas de montagem, testes de homologação, teste de aceitação de fábrica e operação.

A aplicação da tecnologia CAE através do método dos elementos finitos surge como uma ferramenta alternativa para analisar as diferentes formas e aplicações de uma determinada válvula, possibilitando a otimização da mesma com o foco central na agregação de valor e eliminação de desperdícios.

A compreensão do tipo de produto e a abrangência de seus requisitos são elementos essenciais para a avaliação de uma válvula de esfera flutuante por meio da técnica do método dos elementos finitos. No caso de válvulas industriais do tipo flutuante muitos de seus requisitos são normalmente conhecidos e definidos pelos órgãos normalizadores nacionais ou internacionais o que, em muitos casos, simplifica as etapas iniciais do projeto e os tipos de análise a serem adotadas.

Através da análise estrutural realizado no presente estudo, verificou-se a integridade estrutural dos principais componentes da válvula. Este modelo se mostra de grande utilidade no processo de desenvolvimento de válvulas, uma vez que este modelo é eficiente na solução ou na prevenção de problemas que possam ocorrer durante ensaios de homologação e/ou durante a operação.

Referências bibliográficas

ABNT, INMETRO. GUIA para a Expressão da Incerteza de Medição. 3ª Ed., Rio de Janeiro. ABNT, INMETRO, 2003.

ABNT NBR 15827. Válvulas industriais para instalações de exploração, produção, refino e transporte de produtos de petróleo – Requisitos de projeto e ensaio de protótipo, 3ª Edição, Rio de Janeiro: ABNT 2014.

BELL, S. A., Beginner's Guide to Uncertainty of Measurment. 2ª Ed. Middlesex: National Physical Laboratory, 1999.

BIASIBETTI FERNANDO. Otimização de projetos de válvula utilizando os conceitos de projeto de experimentos. Dissertação de M.Sc., PPGEP/UFRGS, Porto Alegre, RS, Brasil, 2013.

COOK, Robert D.; MALKUS, David S.; WITT, Robert J., Concepts and Applications of Finite Element Analysis, 4ª Edição, EUA, Wiley India Pvt Ltda, 2002.

CORT, A., "Safety and Reliability Analysis of Subsea production Equipment: Current Practice and Future Potential", Subsea International Conference, 1994.

FILHO, A. A., Elementos Finitos: A Base da Tecnologia CAE, 4ª Edição. São Paulo, Editora Érica Ltda,2006.

HOFFMANN, KARL., An Introduction to Measurements using Strain Gages, 1ª Edição, Alemanha, Hottinger Baldwin Messtechnik GmbH, 1989.

INMETRO. Portaria Nº 272/ 2011. Requisitos de Avaliação da Conformidade para Válvulas Industriais para Instalações de Exploração, Produção, Refino e Transporte de Produtos de Petróleo.

JCGM. Evaluation of measurement data – Guide to the expression of uncertainty in measurement – GUM.  Paris, 2008.

MATHIAS, ARTHUR C., Válvulas – Tipos, Seleção, Dimensionamento, 1ª Edição, Brasil, Artliber Editora LTDA, 2008.

MORGAN, J.;LIKER J., The Toyota Product Development System - Integrating People, Process and Technology. New York: Productivity Press, 2006

NAKAMURA, ET; AUCAR JUNIOR, J.J.  M; ZANOLLI, J.R; MACHADO, V.W., Desenvolvimento de produtos eletroeletrônicos utilizando ferramentas CAD/CAE/CAM, XXIV Encontro Nac. de Engenheiro de Produção - Florianópolis, SC, Brasil, 03 a 05 de Novembro de 2004.

ROZENFELD, Henrique; FORCELLINI, F. A; AMARAL, D. C; TOLEDO, J. C; SILVA, S. L; ALLIPRANDINI, D. H; SCALICE, R.K; Gestão de Desenvolvimento de Produtos, 1º Edição, São Paulo, Editora Saraiva, 2006.

SALES, H.J. NOBRE FILHO, G.W.L. SANTOS, E.C., Utilização de Software CAD e CAE no Desenvolvimento de Produto Sustentável para Aquecimento de Água. Revista GEINTEC – ISSN: 2237-0722. São Cristóvão/SE – 2013. Vol. 3/n. 5/ p.168-179.

THE AMERICAN SOCIETY OF MECHANICAL ENGINEERS. ASME Section II Part D: ASME Boiler & Pressure Vessel Code: Section II Part D: Properties (Metric): Materials. Nova Iorque: ASME, 2010.

WEISS, JAMES M.G; LIMA, ANTÔNIO M. A., Avaliação da capacitação tecnológica para a produção de válvulas Industriais. 23º Congresso Nacional de Transporte Aquaviário, Construção Naval e Offshore. Rio de Janeiro, 25 a 29 de Outubro de 2010.

WÜTEMBERG, L. M.; LILLIESKÖLD, J.; Ericsson, E., Abstract Model of LPD: A Critical Review of the Lean Product Development Concept. Proceedings Of Picmet 11: Technology Management In The Energy-Smart World (PICMET), p868-874, 2011.

1. Universidade Federal do Rio Grande do Sul – Programa de Pós-Graduação em Engenharia de Minas, Metalúrgica e de Materiais – Porto Alegre-RS, Brasil. E-mail: diegorossetto@utfpr.edu.br
2. Universidade Federal do Rio Grande do Sul – Programa de Pós-Graduação em Engenharia de Minas, Metalúrgica e de Materiais – Porto Alegre-RS, Brasil.
3. Universidade de Caxias do Sul – Centro de Ciências Exatas e Tecnologia Caxias do Sul - Brasil.