Espacios. Vol. 36 (Nº 21) Año 2015. Pág. 8

Otimização de quadro de lotação hospitalar: Aplicação da meta-heurística Busca Tabu

Hospital stocking frame optimization: Application of Tabu Search metaheuristic

Kelly Cristina Ferreira DIAS 1; Leonardo Dagnino CHIWIACOWSKY 2; André Luís KORZENOWSKI 3

Recibido: 06/07/15 • Aprobado: 03/08/2015

Contenido

1. Introdução

2. Referêncial Teórico

3. Materiais e Métodos

4. Modelagem

5. Experimento

6. Conclusões

Referências

1. Introdução

O setor de saúde é formado por diversos atores que podem ser caracterizados como atuando em um sistema complexo e intensivo em conhecimento e tecnologia (ANAHP, 2013). Em particular, é complexa a operação associada ao ator prestador de serviços hospitalares. O termo complexo é usado para designar que uma organização hospitalar necessita desempenhar diversas funções e inter-relações de modo a realizar suas operações, indo além da função fim de restabelecimento do paciente. Outrossim, inclui operações relacionadas à prevenção de doenças, gestão de segurança e risco hospitalar, análise e pesquisa, diagnóstico, tratamento e recuperação de pacientes, além de atividades de assistência a familiares, gestão, hotelaria, estacionamento, manutenção técnica, gestão de cadeia de suprimentos, gestão voltada à regulação de atenção à saúde, capacitação de pessoal e gestão econômico-financeira, entre outras atividades (GAIDZINSKI et al., 2009; LIMA, 2010; GELBCKE, 2011).

Também nesse contexto, a forma como as melhorias dos serviços de saúde são gerenciadas pode fazer a diferença em identificar os fatores que influenciam o comportamento do sistema a fim de associá-los a melhores resultados e desempenho (FUGULIN et al., 2011). Em particular, por se tratarem de organizações intensivas em conhecimento e tecnologia, as rubricas relacionadas a pessoal e equipamentos possuem grande representatividade na estrutura de custos fixos e variáveis do ambiente hospitalar.

No Brasil, a gestão de quadros de pessoal é regulada por normativas trabalhistas (COFEN, 2004; GELBCKE et al., 2012; ROSSETTI et al., 2014), que contemplam aspectos relacionados às atribuições e competências das diferentes categorias do profissional de saúde, bem como a duração dos turnos e dos intervalos entre turnos de trabalho. Essa regulação gera complexidades de gestão quando considerada a variabilidade intrínseca das atividades assistenciais de saúde, relacionadas a aspectos epidemiológicos, sazonais ou eventuais. Essa perspectiva, ainda que justificada, gera pressão sobre os quadros de pessoal, reforçando a necessidade de adequada gestão sobre essa dimensão da organização, de modo a reduzir os impactos sobre os custos da operação.

Considerados os argumentos previamente apresentados, organizações hospitalares têm sido compelidas – desde há muito tempo – a planejar cronogramas e escalas de trabalho buscando utilizar o seu quadro de pessoal da forma mais eficiente possível(BURKE; LI; et al., 2012; SMET et al., 2014; WU et al., 2015). As exigências podem variar de setor para setor ou de acordo com a natureza do serviço de atenção à saúde, mas se mantém o objetivo principal de encontrar uma programação que garanta uma cobertura adequada em todos os momentos, contemplando aspectos de risco de oferta de capacidade em função de fontes de variabilidade. A variedade de escalas de trabalho, requisitos técnicos específicos dos diferentes níveis de cobertura de serviços e em diferentes graus, folgas semanais ou entre turnos, e a distribuição de recursos em diferentes turnos, além de aspectos intangíveis relacionados às atividades desempenhadas, representam dimensões relevantes ao problema e sustentam a visão de complexidade associada à obtenção de soluções satisfatórias e robustas (DOWSLAND, 1998; JUNIOR, 2002; BURKE, EDMUND K.; CURTOIS, 2014).

Esse problema, genericamente denominado de Problema do Quadro de Lotação (QL) também visto na literatura como Rostering (PUENTE et al., 2009; BURKE; BAI; et al., 2010; ABOBAKER et al., 2011; PASCHOU et al., 2015), Timetabling (BURKE; JIM NEWALL, 2004; BURKE et al., 2011; BURKE; KENDALL; et al., 2012; BÄUMELT et al., 2014) tem recebido atenção da área de Pesquisa Operacional, por também encontrar aplicações similares em contextos de Aviação Civil (ATKIN et al., 2008, 2011; BERGH et al., 2013; BÄUMELT et al., 2014; SALAZAR-GONZÁLEZ, 2014), Educação (FRANCISCO, 2013) e Call center (SOUZA, 2010; ÖRMECI et al., 2014). Em especial, a alocação de equipes hospitalares mostra-se relevante dado que o controle dos custos associados ao pessoal não pode comprometer a qualidade do atendimento (ERNST, A.T. et al., 2004; GAIDZINSKI et al., 2009; SOUZA, 2010; FUGULIN et al., 2011; ÖRMECI et al., 2014).

Devido ao grande número de variáveis e restrições envolvidas, o problema é classificado como NP-hard, significando que métodos tradicionais de computação não atingem resultados satisfatórios e que os esforços de computabilidade da solução variam pelo menos exponencialmente em função do número de variáveis tratadas (HARTMANIS; LEEUWEN, 1969; BURKE; CAUSMAECKER, 2001; NAUDIN et al., 2009; BURKE; LI; et al., 2010; GLASS; KNIGHT, 2010; BURKE et al., 2011, 2012; LI et al., 2011; MAENHOUT; VANHOUCKE, 2011; AWADALLAH et al., 2013; WRIGHT; MAHAR, 2013; MARTIN et al., 2013). Com a intenção de solucionar essa classe de problema, uma proliferação de técnicas de otimização pode ser observada, adaptando-se conceitos de outras áreas na busca para desenvolver procedimentos mais eficientes (GLOVER et al., 1993; GLOVER; KOCHENBERGER, 2003; HILLIER; LIEBERMAN, 2013). Casos reais do problema têm sido tratados com algumas meta-heurísticas, tais como: Simulated Annealing (ABOBAKER et al., 2011), Busca Tabu (BURKE et al., 1999, 2004) Vizinhança Variável (GLASS; KNIGHT, 2010; BILGIN et al., 2010), Heurísticas baseadas em componentes (LI et al., 2009), Busca Harmônica (HADWAN et al., 2013) e Hiper-Heurísticas (LI et al., 2011; BURKE; KENDALL; et al., 2012; MISIR et al., 2013; BURKE et al., 2013) e Algoritmos Genéticos (PUENTE et al., 2009). Meta-heurísticas são procedimentos computacionais e matemáticos que possuem uma definição geral e são implementados com adaptações para tratar de um problema específico. Considerado o exposto, este trabalho propõe um modelo para solucionar o problema de lotação de quadro da equipe utilizando a meta-heurística Busca Tabu (BT) (HILLIER; LIEBERMAN, 2013).

Como base para o estudo, estabeleceu-se a modelagem com base em dados do contexto real de uma Unidade de Internação de um hospital de grande porte, localizado na região metropolitana de Porto Alegre, Rio Grande do Sul. ao  referida Unidade conta com 253 técnicos de enfermagem e 56 enfermeiros , além disso possui 224 leitos, atendendo pacientes com diferentes patologias. Objetiva-se, assim, estabelecer bases para um modelo de solução do problema de forma evolutiva. Dessa forma, o estudo contempla as normativas/restrições operacionais e legais que devem ser consideradas em um hospital no Brasil, considerando as particularidades do hospital em estudo. O objetivo do modelo é obter o melhor aproveitamento da equipe do setor. Para sustentar o objetivo proposto, a seguir apresentam-se conceitos relacionados ao problema de QL no contexto hospitalar, seguido de uma breve explanação sobre a meta-heurística Busca Tabu. Após, é apresentada a modelagem proposta, e um caso de aplicação. Então, os resultados e limitações identificados na solução proposta são apresentados, e algumas considerações, a título de conclusão finalizam o artigo.

2. Referêncial Teórico

2.1. O problema de quadro de lotação hospitalar

A literatura aborda o problema de Quadro de Lotação como um problema de gerar cronogramas de equipe viáveis, para um grupo de funcionários que trabalham em conjunto para fornecer algum serviço (DOHN; MASON, 2013). O processo inicia com o seu dimensionamento, uma vez que é preciso prever a quantidade de enfermeiros, com competências específicas para cada categoria necessária a fim de atender as necessidades dos pacientes de cada enfermaria.

Dimensionar o pessoal de enfermagem é realizar a previsão da quantidade de funcionários por categoria, requerida para atender, direta ou indiretamente, às necessidades de assistência de enfermagem da clientela (POLTOSI, 2007). O dimensionamento inadequado aumenta custos ou prejudica a qualidade da assistência prestada. A inadequação numérica e qualitativa dos recursos humanos da enfermagem prejudica os pacientes dos serviços de saúde no seu direito de assistência à saúde livre de riscos. Essa inadequação também pode comprometer legalmente a instituição, por falhas ocorridas na assistência (GAIDZINSKI, 1998).

A escala de trabalho de pessoal é o processo de distribuição da equipe de enfermagem, previamente dimensionada, nos turnos do cronograma de trabalho definido, de modo que o hospital possa satisfazer a demanda de atendimento ao paciente, seguindo sempre as normativas e as regulamentações associadas aos contratos de trabalho que devem ser observadas durante o processo (BURKE, LI, et al., 2010; ERNST et al., 2004). O cronograma deve incluir, para cada membro da equipe, a sequência de turnos e dias de folga para ser trabalhado durante o período. Este cronograma deve satisfazer as restrições de demanda pré-especificados que normalmente expressam requisitos mínimos de pessoal ou períodos de tempo, e podem incluir requisitos para o pessoal com certas habilidades ou o cumprimento de determinadas condições do contrato (ERNST, A. T. et al., 2004).

Nos hospitais, as equipes de enfermagens são representadas por enfermeiros e técnicos de enfermagem. A enfermagem é uma profissão que possui atribuições bem definidas. São os enfermeiros, na concepção geral, que cuidam dos pacientes internados nos hospitais ou clínicas, acompanhando o estado de saúde do paciente diariamente. Controlam o uso e a distribuição de material médico-hospitalar, providenciam que os medicamentos sejam ministrados conforme a prescrição dos médicos. Aplicam injeções, soros e fazem curativos (POLTOSI, 2007).

A elaboração da escala de trabalho para as equipes de enfermagem seguem um padrão de dias de trabalho e de folga que são designados a um membro da equipe. Deve cumprir os requisitos operacionais para um determinado período. Se D é o número de dias do período sendo planejado e o trabalhador pode ser designado a T turnos diferentes a cada dia, então TD são escalas a serem examinadas (POLTOSI, 2007). Considerando que cada dia da escala D pode assumir os valores "trabalho (1)" ou "folga (0)", para um dia existem dois escalas possíveis, já para uma semana, ou seja, sete dias, são 128 resultados aceitáveis, e para duas semanas as combinações chegam a 16.384 possibilidades de escalas diferentes (POLTOSI, 2007). Além disso, o problema Quadro de Lotação envolve muitas restrições, que podem ser obrigatórias ou desejáveis.

2.2. A meta-heurística Busca Tabu

A forma básica do algoritmo de Busca Tabu está fundamentada nas ideias propostas por (GLOVER; KOCHENBERGER, 2003). O algoritmo é baseado em procedimentos heurísticos que permitem explorar o espaço de busca e encontrar novas soluções além daquelas encontradas em uma busca local(GLOVER, 1989, 1990; HILLIER; LIEBERMAN, 2013). A Busca Tabu pode ser vista como um método iterativo de procura de uma nova solução, não necessariamente melhor do que outras identificadas anteriormente, na vizinhança da atual solução, com vista a obter uma solução global do problema (ótimo global), e não apenas local. Essa procura acontece por meio de movimentos repetidos de uma solução (s) para outra solução (s*) localizada na vizinhança (N) de s. Esses movimentos são realizados com o objetivo de chegar a uma solução eficiente que pode ser qualificada como "boa" (ótima ou quase ótima) pela avaliação de uma função objetivo (f) a ser minimizada ou maximizada (POLTOSI, 2007)

Essa é uma meta-heurística de busca não-monotônica, cuja característica principal é a capacidade de incorporar uma estrutura de memória adaptativa que proíbe ou penaliza movimentos que retornem a uma solução visitada recentemente ou já identificada como subótima. Uma característica essencial deste método é a manutenção de uma lista de movimentos proibidos conhecida como Lista Tabu, a qual exerce um papel fundamental no processo de pesquisa de soluções reduzindo o risco de ciclagem (execução em ciclo infinito) do algoritmo(GLOVER, 1989, 1990; GLOVER; KOCHENBERGER, 2003).

Na prática, para compreender melhor sua utilidade torna-se necessário detalhar seu fluxo de execução. Para isso, considera-se a existência de uma solução inicial qualquer (s0) para o problema sendo tratado. Estabelece-se uma lista de soluções S e busca-se uma solução em N(s0). A nova solução é identificada e avaliada. Se a próxima f de seu objetivo, é acrescentada em S. A cada iteração, uma nova solução é buscada em N(s). Por outro lado, enquanto o número de iterações sem identificação de melhora em f não atingir um valor máximo parametrizado maxiter, o método pesquisa pelo melhor vizinho da solução corrente de maneira que o movimento realizado para gerar a solução vizinha não esteja contido na lista tabu.

Por meio de outra lista, a Busca Tabu mantém registro dos últimos passos realizados a fim de evitar a volta a uma solução visitada anteriormente. Esse movimento se limita a um horizonte de memória de curto prazo (GLOVER, 1989, 1990). A memória também é utilizada na Busca Tabu em um tipo de processo de aprendizagem: ter visitado várias soluções, que é considerada útil para observar se as boas soluções visitadas até agora têm algumas propriedades comuns (tais como a presença ou ausência de certos elementos). Isso gera um esquema de intensificação para a pesquisa (GLOVER, 1989, 1990). No entanto, a Intensificação, por si só, é insuficiente para produzir os melhores resultados para as classes de problemas de otimização. A diversificação deve ser utilizada para permitir uma pesquisa mais eficiente sobre o conjunto X. Assim, a longo prazo, a busca tabu induz uma alternância entre sequências de passos que intensificam em uma região promissora e passos que diversificam a busca em todas as regiões contrastantes da pesquisa (GLOVER, 1989, 1990).

3. Materiais e Métodos

O delineamento desta pesquisa segue as etapas propostas por Cauchick et al. (2012), baseada em Bertrand e Fransoo (2002), conforme Figura 1.

Figure 1 : Processo de modelagem

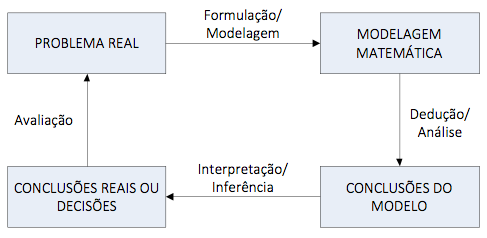
Fonte: Adaptado de (CAUCHICK et al., 2012).

A proposta de Cauchick et al. (2012), ilustra um processo simplificado da abordagem de solução de um problema utilizando formulação/modelagem matemática. As deduções/análises resultantes da modelagem matemática admitem conclusões do modelo e interpretações/inferências da situação real.

Este trabalho foi realizado a partir da identificação de um problema real no Quadro de Lotação em um hospital de Porto Alegre. Para entender o problema e verificar como este vem sendo tratado, foi realizado a revisão da literatura conforme as seções 1 e 2. Além disso, foram realizadas visitas e entrevistas in loco objetivando compreender o problema no ambiente da pesquisa.  

Conhecido o problema real, a etapa seguinte consistiu em propor um modelo matemático baseado nas restrições especificas do setor em análise, conforme seção 4. A seção 4 ainda tratou da etapa de Aplicação do modelo, aplicando técnicas matemáticas e tecnologia computacional para resolver o modelo e visualizar as conclusões e/ou decisões sugeridas pelo mesmo. Por fim, a seção 5 foi dedicada à experimentação do modelo.

4. Modelagem

Os problemas de escalonamento de pessoal tratam da devida apropriação da necessidade de alocação e designação de tarefas à uma equipe de trabalho, levando em consideração os requisitos internos e externos de uma organização. A elaboração das escalas de trabalho envolve a alocação de pessoal a períodos de tempo e locais (POLTOSI, 2007).

Uma escala semanal de colaboradores apresenta a distribuição da equipe de uma Unidade de Internação, considerando duas semanas do mês e os turnos de trabalho: geralmente, manhã, tarde e noite. Na escala, também são registradas as folgas. A escala semanal tem a estrutura de uma matriz bidimensional onde cada linha corresponde à escala de um colaborador, também chamada de escala individual, e as colunas representam os dias divididos em turnos do período que está sendo considerado. A Figura 2 apresenta um modelo de escala mensal.

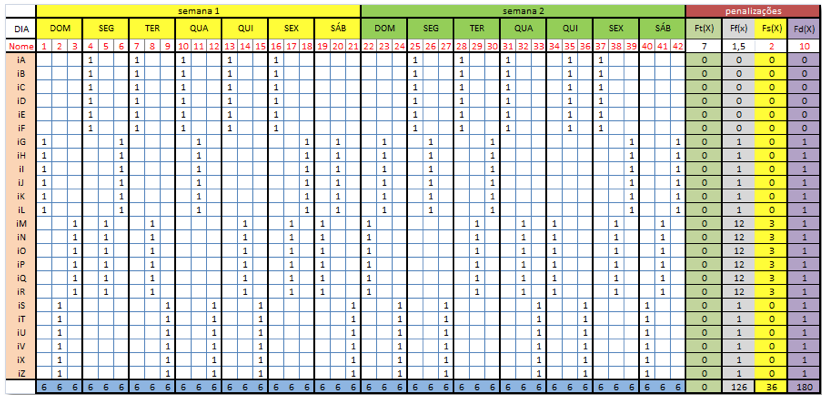
Figure 2 : Quadro de Escala de trabalho – Unidade de Internação

Na geração da escala semanal, de modo a obter-se resultados de boa qualidade, devem ser considerados a legislação trabalhista, as normas da instituição, as regras e dinâmica do Centro Cirúrgico, bem como as características da clientela e da equipe.

As restrições obrigatórias são aquelas que devem ser atendidas para que uma escala seja viável. Neste trabalho foi considerada como obrigatória a seguinte restrição (ERNST. et al., 2004):

1. Cobertura mínima: Cada turno deve ter o pessoal designado de forma a garantir a demanda mínima de 6 funcionários por turno.

As restrições desejáveis, por sua vez, representam um conjunto de fatores que contribuem para adequar o modelo à aplicação. Neste aspecto, na modelagem elas são passíveis de relaxação. É praticamente impossível encontrar uma escala que atenda a todos as requisitos desejáveis (POLTOSI, 2007; BURKE, EDMUND KIERAN; CURTOIS, 2014) e que são freqüentemente conflitantes. As restrições desejáveis propostas nesse trabalho foram:

1. Função Turnos (Ft(X)): uma pessoa deve ser designada a no máximo 1 turno por dia.
2. Função Folgas (Ff(X)): Deve ser concedido duas folgas entre um período de sete dias.
3. Função Sequencia (Fs(X)): Não deve-se trabalhar mais do que cinco dias consecutivos.
4. Função Domingo (Fd(X)): No mínimo um sábado ou domingo de folga a cada 2 semanas.

A função objetivo (FO) avalia a qualidade da solução indicando o quanto as restrições desejáveis estão sendo satisfeitas. A cada uma das restrições é atribuído um peso, que influenciará na importância desta variável no resultado. Para entendimento da formulação matemática do modelo proposto, segue a lista de símbolos na Tabela 1.

A formulação matemática proposta é apresentada nas equações (1) e (2).

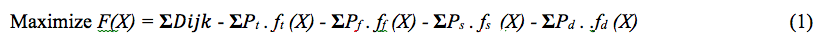
sujeito a

Tabela 1 : Lista de símbolos da formulação matemática do modelo proposto.

A restrição obrigatória é garantida pela formulação (2), que garante os requisitos de cobertura mínima. A função objetivo (1) é composta por quatro variáveis de decisão, representadas por funções, multiplicadas pelos respectivos pesos. As funções Turnos, Folgas, Sequencia e Domingo  são calculadas para cada técnico, representados nas linhas da escala, e somadas para integrarem a função objetivo. A função Cobertura examina os dias do período da escala, que estão dispostos nas colunas da escala.

Os métodos e procedimentos utilizados para a resolução do Problema de quadro de lotação estão subdivididos em dois momentos. O primeiro corresponde à geração de uma solução inicial de relativa qualidade e o segundo está relacionado à aplicação da meta-heurística Busca Tabu, com o objetivo de aprimorar a solução inicialmente estabelecida. A solução inicial pode ser qualquer solução que chamamos factível por coluna, isto é, que sejam respeitadas todas as restrições obrigatórias do setor para cada turno e colaborador considerado. Mesmo que essa primeira solução seja muito ruim, ela é de extrema importância para a alocação, pois, é a nela que está determinado o número de turnos para cada dia do nosso horizonte. O objetivo de tal solução é somente que ela sirva como solução inicial (GLOVER, 1989, 1990; GLOVER et al., 1993; LAGUNA, 1994).

No segundo momento, de aplicação da meta-heurística, o período Tabu é definido como o número de iterações que uma determinada solução permanece como Tabu, ou seja, período no qual está proibido (tabu) alteração na solução local. A definição do período tabu é um elemento essencial para a eficiência da busca, pois, períodos muito curtos podem gerar ciclos, já os longos podem prejudicar a solução (GLOVER, 1989, 1990; GLOVER et al., 1993; LAGUNA, 1994; HILLIER; LIEBERMAN, 2013). Neste modelo foi utilizado o Período Tabu estático, ou seja, durante todas as buscas, os elementos já visitados, permanecem na lista por 3 ciclos. O critério de parada da Busca Tabu, assim como em outras meta-heuristicas, pode ser a partir de um numero fixo de iterações sem melhoria da solução (HILLIER; LIEBERMAN, 2013). Neste modelo foi estipulado como critério de parada dez iterações para teste.

O algoritmo da Busca Tabu na sua forma mais simples pode ser representado em 6 passos de acordo com o pseudocódigo na Figura 3.

Figura 3 : pseudocódigo Busca Tabu

5. Experimento

O experimento aqui realizado não objetiva uma solução real nem a melhor solução possível de um caso hipotético, mas busca exemplificar uma aplicação da meta-heurística busca tabu na solução de um problema frequentemente encontrado. O cenário criado procura uma solução de melhoria para alocação de funcionários em uma Unidade de Internação que funciona 24h por dia, devendo em cada um dos 3 turnos do dia ter 6 funcionários trabalhando (restrição obrigatória). O setor conta com 24 colaboradores.

O experimento limitou o período da análise em duas semanas e o número de iterações em 10, valores suficientes para demonstrar a aplicação da BT. A determinação dos pesos de cada penalidade foram inicialmente calibrados através de testes aleatórios que buscaram equilibrar as punições que compõem a função objetivo.

O período tabu e o critério de parada são determinações importantes para a aplicação da BT e dos registros das iterações na LT. No entanto, Para este experimento os registros foram realizados, mas considerando o limite de iterações propostos, 10, e a quantidade de testes possíveis, não foi preocupação esses itens. Atendendo ao que é exigência para aplicação da BT, uma solução inicial factível qualquer foi determinada. Com a utilização do software Microsoft Excel©, foi possível obter valores de penalidades em cada linha e, consequentemente, o valor numérico da função objetivo da solução inicial. A utilização da planilha eletrônica apenas facilitou encontrar o resultado final, o que exigiria árduo trabalho na hipótese de realização manual.

Após as iterações em acordo as proposições da BT, foi possível perceber significativa redução do valor numérico da FO, inicialmente com -90 e após as iterações, com -24, alcançando-se o objetivo de demonstrar o funcionamento desta meta-heurística. A Figura 2 representa a situação inicial e a Figura 4 a solução após as iterações. Na Figura 5, que representa a Lista Tabu, está o registro das iterações e o resultado da Função Objetivo alcançado. As cores que identificaram cada iteração na Figura 5 estão registradas de forma equivalente na Figura 4, que pode também representar o tabu criado a cada iteração.

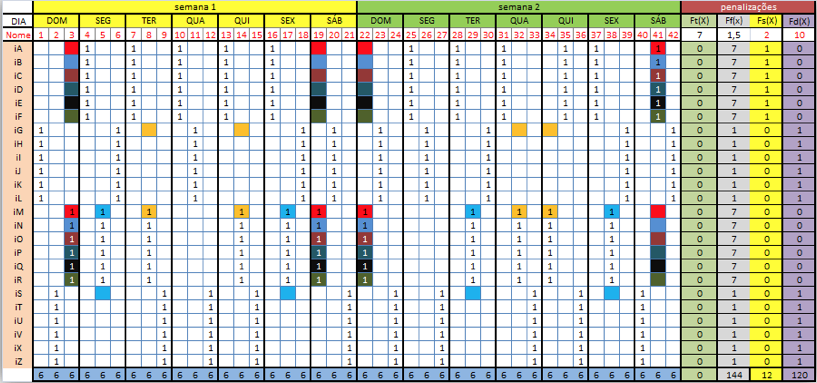
Figura 4 - Quadro de Escala de trabalho – Centro Cirúrgico após iterações.

-----

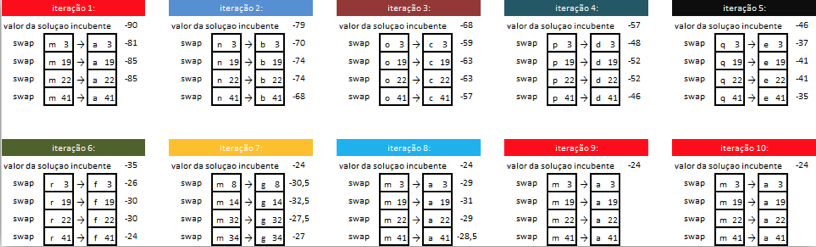
Figura 5 - Iterações realizadas.

6. Conclusões

A aplicação de um modelo de otimização combinatória para aplicação no problema do quadro de lotação de enfermeiros tem sido foco de estudos como apresentado no referêncial. Este trabalho contribuí ao utilizar a meta-heurística Busca Tabu para o problema. Foi possível evidenciar que o modelo aqui proposto demonstra contribuir para solução do problema apresentado, pois foi observado melhoria nos resutados advindos do quadro de lotação após as iterações. Além disso, o trabalho mostra a aplicação da Busca Tabu realizada a partir do software Microsoft Excel, mesmo que este seja um problema NP-Hard, o que, de certo modo, pode auxiliar nas aplicações deste tipo de método à gestores com restição ao uso de softwares mais robustos de otimização.

Para estudos futuros, ou até mesmo para aplicação do modelo, seria importante a criação de um recurso computacional, podendo assim, automatizar ainda mais o processo e aumentar o número de iterações, exigindo menor intervenção do gestor na utilização da ferramenta.

Referências

ABOBAKER, R. A.; AYOB, M.; HADWAN, M. Greedy Constructive Heuristic and Local Search Algorithm for Solving Nurse Rostering Problems. 3rd Conference on Data Mining and Optimization (DMO). Anais... . p.28–29, 2011. Selangor, Malaysia.

ANAHP – Associação Nacional de Hospitais Privados. Observatório ANAHP 2013. . Disponível em: <http://anahp.com.br/produtos/revistaobservatório/observatório-anahp-2013.>. .

ATKIN, J. A. D.; BURKE, E. K.; GREENWOOD, J. S. A comparison of two methods for reducing take-off delay at London Heathrow airport. Journal of Scheduling, v. 14, n. 5, p. 409–421, 2011.

ATKIN, J. A. D.; BURKE, E. K.; GREENWOOD, J. S.; REESON, D. On-line decision support for take-off runway scheduling with uncertain taxi times at London Heathrow airport. Journal of Scheduling, v. 11, n. 5, p. 323–346, 2008.

AWADALLAH, M. A.; KHADER, A. T.; AL-BETAR, M. A.; BOLAJI, A. L. Global best Harmony Search with a new pitch adjustment designed for Nurse Rostering. Journal of King Saud University - Computer and Information Sciences, v. 25, n. 2, p. 145–162, 2013.

BÄUMELT, Z.; ŮCHA, P.; HANZÁLEK, Z. A multistage approach for an employee timetabling problem with a high diversity of shifts as a solution for a strongly varying workforce demand. Computers and Operations Research, v. 49, p. 117–129, 2014.

BERGH, J. VAN DEN; BRUECKER, P. DE; BELIËN, J.; BOECK, L. DE; DEMEULEMEESTER, E. A three-stage approach for aircraft line maintenance personnel rostering using MIP, discrete event simulation and DEA. Expert Systems with Applications, v. 40, n. 7, p. 2659–2668, 2013. Elsevier Ltd.

BERTRAND, J. W. M.; FRANSOO, J. C. Operations management research methodologies using quantitative modeling. International Journal of Operations & Production Management, v. 22, n. 2, p. 241–264, 2002.

BILGIN, B.; CAUSMAECKER, P.; ROSSIE, B.; BERGHE, G. VANDEN. Local search neighbourhoods for dealing with a novel nurse rostering model. Annals of Operations Research, v. 194, n. 1, p. 33–57, 2010.

BURKE, E. K.; BAI, R.; BURKE, E. K.; et al. A hybrid evolutionary approach to the nurse rostering problem. IEEE Transactions on Evolutionary Computation, v. 14, n. 4, p. 580–590, 2010.

BURKE, E. K.; CAUSMAECKER, P. DE. Variable Neighbourhood Search for Nurse Rostering Problems. In Metaheuristics International Conference – MIC'2001. Anais... . p.755–760, 2001. Porto, Portugal: In Metaheuristics International Conference – MIC'2001.

BURKE, E. K.; CAUSMAECKER, P. DE; BERGHE, G. VANDEN. A Hybrid Tabu Search Algorithm for the Nurse Rostering Problem. Simulated Evolution and Learning, p. 187–194, 1999.

BURKE, E. K.; CURTOIS, T. New approaches to nurse rostering benchmark instances. European Journal of Operational Research, v. 237, n. 1, p. 71–81, 2014. Elsevier B.V.

BURKE, E. K.; CURTOIS, T. New approaches to nurse rostering benchmark instances. European Journal of Operational Research, v. 237, n. 1, p. 71–81, 2014.

BURKE, E. K.; GENDREAU, M.; HYDE, M.; et al. Hyper-heuristics: a survey of the state of the art. Journal of the Operational Research Society, v. 64, n. 12, p. 1695–1724, 2013.

BURKE, E. K.; JIM NEWALL. Solving Examination Timetabling Problems through Adaption of Heuristic Orderings. Operations Research, v. 129, p. 107–134, 2004.

BURKE, E. K.; KENDALL, G.; MISIR, M.; ÖZCAN, E. Monte Carlo hyper-heuristics for examination timetabling. Annals of Operations Research, v. 196, n. 1, p. 73–90, 2012.

BURKE, E. K.; KENDALL, G.; SOUBEIGA, E. A Tabu-Search Hyperheuristic for Timetabling. Journal of Heuristics, p. 451–470, 2004.

BURKE, E. K.; LI, J.; CURTOIS, T.; PETROVIC, S.; QU, R. The falling tide algorithm: A new multi-objective approach for complex workforce scheduling. Omega, v. 40, n. 3, p. 283–293, 2012. Elsevier.

BURKE, E. K.; LI, J.; QU, R. A hybrid model of integer programming and variable neighbourhood search for highly-constrained nurse rostering problems. European Journal of Operational Research, v. 203, n. 2, p. 484–493, 2010. Elsevier B.V.

BURKE, E. K.; PHAM, N.; QU, R.; YELLEN, J. Linear combinations of heuristics for examination timetabling. Annals of Operations Research, v. 194, n. 1, p. 89–109, 2011.

CAUCHICK, P. A.; FLEURY, A.; PEREIRA MELLO, C. H.; et al. Capítulo 8 – Modelagem e Simulação. Metodologia De Pesquisa Em Engenharia De Produção. p.169–198, 2012.

CONSELHO FEDERAL DE ENFERMAGEM - COFEN. Resolução 293 de 21 de Setembro de 2004. . Rio de Janeiro, Brasil.

DOHN, A.; MASON, A. Branch-and-price for staff rostering: An efficient implementation using generic programming and nested column generation. European Journal of Operational Research, v. 230, n. 1, p. 157–169, 2013.

DOWSLAND, K. A. Nurse scheduling with tabu search and strategic oscillation. European Journal of Operational Research, v. 106, p. 393–407, 1998.

ERNST, A. T.; JIANG, H.; KRISHNAMOORTHY, M.; OWENS, B.; SIER, D. An Annotated Bibliography of Personnel Scheduling and Rostering. Annals of Operations Research, v. 127, n. 1-4, p. 21–144, 2004.

ERNST, A. T.; JIANG, H.; KRISHNAMOORTHY, M.; SIER, D. Staff scheduling and rostering: A review of applications, methods and models. European Journal of Operational Research. Anais... . v. 153, p.3–27, 2004.

FRANCISCO, D. O. Aplicação de Algoritmos Bio-Inspirados ao Problema de Geração Automática de Grades Horárias, 2013. Dissertação de Mestrado em Ciências, Programa de Engenharia Elétrica - USP.

FUGULIN, F. MARIA TOGEIRO; LIMA, A. F. COSTA; CASTILHO, V.; et al. Custo da adequação quantitativa de profissionais de enfermagem em Unidade Neonatal. Revista da Escola de Enfermagem USP, v. 45, p. 1582 – 1588, 2011.

GAIDZINSKI, R. R. Dimensionamento de pessoal de enfermagem em instituições hospitalares, 1998. Tese para Doutorado em Enfermagem. Universidade de São Paulo.

GAIDZINSKI, R. R.; MARIA, F.; FUGULIN, T.; et al. Dimensionamento informatizado de profissionais de enfermagem: inovação tecnológica. Revista da Escola de Enfermagem USP, v. 43, n. 2, p. 1314–1319, 2009.

GELBCKE, F. L. Carga de trabalho na enfermagem: variável do dimensionamento de pessoal. Enfermagem em Foco, v. 2, n. 3, p. 6–9, 2011.

GELBCKE, F. L.; MATOS, E.; SCHMOELLER, R.; MESQUITA, M. P. L. DE; BENEDET, S. A. Instrumento para classificação do grau de dependência de usuários: um estudo para contribuir no dimensionamento de pessoal. Enfermagem em Foco, v. 3, n. 1, p. 25–28, 2012.

GLASS, C. A.; KNIGHT, R. A. The nurse rostering problem: A critical appraisal of the problem structure. European Journal of Operational Research, v. 202, n. 2, p. 379–389, 2010. Elsevier B.V.

GLOVER, F. Tabu Search_PartI. ORSA Journal on Computing, v. 1, n. 3, p. 190 –207, 1989.

GLOVER, F. TS - Tutorial. 1990.

GLOVER, F.; KOCHENBERGER, G. A. Handbook of Metaheuristcs. Kluwer Academic Publishers, 2003.

GLOVER, F.; TAIUARD, E.; WERRA, D. DE. Tabu Search: An introduction. Operations Research, v. 41, p. 3–28, 1993.

HADWAN, M.; AYOB, M.; SABAR, N. R.; QU, R. A harmony search algorithm for nurse rostering problems. Information Sciences, v. 233, p. 126–140, 2013.

HARTMANIS, J.; LEEUWEN, J. VAN. Lecture Notes in Computer Science. In: Springer (Ed.); , 1969. Eleventh Annual International Symposium on Algorithms and Computation (ISAAC 2000).

HILLIER, F. S.; LIEBERMAN, G. J. Introdução à pesquisa operacional. 9o ed. Porto Alegre: AMGH, 2013.

JUNIOR, J. E. P. Esquematização de médicos em salas de emergências: Uma abordagem HíbridaDissertação, 2002. Universidade Estadual de Campinas Instituto de Matemática, Estatística e Departamento de Matemática Aplicada.

LAGUNA, M. A Guide to Implementing Tabu Search. Investigacion Operativa, v. 4, n. 1, p. 5–25, 1994.

LI, J.; AICKELIN, U.; BURKE, E. K. A Component Based Heuristic Search Method with Evolutionary Eliminations for Hospital Personnel Scheduling. INFORMS Journal on Computing, v. 21, n. 3, p. 468–479, 2009.

LI, J.; BURKE, E. K.; QU, R. Integrating neural networks and logistic regression to underpin hyper-heuristic search. Knowledge-Based Systems, v. 24, n. 2, p. 322–330, 2011. Elsevier B.V.

LIMA, L. B. DE. Nursing activities score para avaliação da carga de trabalho de enfermagem em unidade de recuperação pós-anestésicaUFRGS, 2010. Dissertação de Mestrado em Enfermagem. UFRGS.

MAENHOUT, B.; VANHOUCKE, M. An evolutionary approach for the nurse rerostering problem. Computers & Operations Research, v. 38, n. 10, p. 1400–1411, 2011.

MARTIN, S.; OUELHADJ, D.; SMET, P.; BERGHE, G. VANDEN; ÖZCAN, E. Cooperative search for fair nurse rosters. Expert Systems with Applications, v. 40, n. 16, p. 6674–6683, 2013. Elsevier Ltd.

MISIR, M.; VERBEECK, K.; CAUSMAECKER, P. DE; BERGHE, G. VANDEN. An investigation on the generality level of selection hyper-heuristics under different empirical conditions. Applied Soft Computing, v. 13, n. 7, p. 3335–3353, 2013.

NAUDIN, É.; CHAN, P. Y. C.; HIROUX, M.; ZEMMOURI, T.; WEIL, G. Analysis of three mathematical models of the Staff Rostering Problem. Journal of Scheduling, v. 15, n. 1, p. 23–38, 2009.

ÖRMECI, E. L.; SALMAN, F. S.; YÜCEL, E. Staff rostering in call centers providing employee transportation. Omega, v. 43, p. 41–53, 2014.

PASCHOU, M.; PAPADIMITIRIOU, C.; NODARAKIS, N.; et al. Enhanced healthcare personnel rostering solution using mobile technologies. Journal of Systems and Software, v. 100, p. 44–53, 2015.

POLTOSI, M. R. Elaboração de escalas de trabalho de técnicos de enfermagem com Busca Tabu e Algoritmos Genéticos, 2007. Dissertação de Mestrado em Computação Aplicada. Universidade do Vale do Rio dos Sinos - UNISINOS.

PUENTE, J.; GÓMEZ, A.; FERNÁNDEZ, I.; PRIORE, P. Medical doctor rostering problem in a hospital emergency department by means of genetic algorithms. Computers & Industrial Engineering, v. 56, n. 4, p. 1232–1242, 2009.

ROSSETTI, A. C.; GAIDZINSKI, R. R.; BRACCO, M. M. Determinação da carga de trabalho e do dimensionamento da equipe de enfermagem em um pronto-socorro pediátrico. Einstein (São Paulo, Brazil), v. 12, n. 11, p. 217–22, 2014.

SALAZAR-GONZÁLEZ, J. Approaches to solve the fl eet-assignment , aircraft-routing , crew-pairing and crew-rostering problems of a regional carrier. Omega, v. 43, p. 71–82, 2014.

SMET, P.; BILGIN, B.; CAUSMAECKER, P. DE; BERGHE, G. VANDEN. Modelling and evaluation issues in nurse rostering. Annals of Operations Research, v. 218, p. 303–326, 2014.

SOUZA, R. A. DE. Otimização das escalas de trabalho dos atendentes e dimensionamento de um call center receptivo, 2010. Tese de Doutorado em Engenharia de Produção. Universidade Federal de Santa Catarina.

WRIGHT, P. D.; MAHAR, S. Centralized nurse scheduling to simultaneously improve schedule cost and nurse satisfaction. Omega (United Kingdom), v. 41, n. 6, p. 1042–1052, 2013. Elsevier. Disponível em: <http://dx.doi.org/10.1016/j.omega.2012.08.004>. .

WU, T.-H.; YEH, J.-Y.; LEE, Y.-M. A particle swarm optimization approach with refinement procedure for nurse rostering problem. Computers & Operations Research, v. 54, p. 52–63, 2015.

1. PPG em Engenharia de Produção e Sistemas Universidade do Vale do Rio dos Sinos – UNISINOS

2. PPG em Engenharia de Produção e Sistemas / PPG em Computação Aplicada Universidade do Vale do Rio dos Sinos - UNISINOS

3. PPG em Engenharia de Produção e Sistemas Universidade do Vale do Rio dos Sinos - UNISINOS. Email: akorzenowski@unisinos.br