![]() Espacios. Vol. 36 (Nº 18) Año 2015. Pág. E-2
Espacios. Vol. 36 (Nº 18) Año 2015. Pág. E-2
Desempenho Acadêmico na Disciplina de Cálculo em Cursos de Engenharia
Academic performance in the calculation of Discipline Engineering courses
Renata Feuser SILVEIRA 1; Antonio José dos SANTOS 2
Recibido: 02/06/2015 • Aprobado: 18/07/2015
Contenido
4 Análise Estatística da Não Aprovação dos Estudantes
RESUMO: Este artigo promove uma análise e reflexão sobre as possíveis causas do alto índice de alunos não-aprovados na disciplina de cálculo I dos cursos de engenharia, no ensino superior. A pesquisa foi realizada com alunos de duas turmas de um Centro Universitário da região sul do Brasil, cujo nome não será revelado visando preservar a imagem dessa instituição de ensino. Durante o estudo foram elencados fatores que contribuem para o aumento desse índice e os obstáculos de natureza didática. Mundialmente, pesquisas no âmbito da educação matemática vêm se avolumando e por essa razão cada vez mais é oportuno o desenvolvimento de estudos que propiciem o levantamento e a análise dos resultados e indicação de novas direções para futuros pesquisadores. |
ABSTRACT: This paper promotes an analysis and reflection on the possible causes of the high rate of unapproved students on I calculation discipline of engineering courses in higher education. The survey was conducted with students from two classes of a University Center of Southern Brazil, whose name will not be revealed in order to preserve the image of this educational institution. During the study were listed factors contributing to the increase of this index and the didactic obstacles. Worldwide, research within mathematics education are growing and therefore is increasingly appropriate to the development of studies that provide the survey and analyzing the results and indicating new directions for future researchers. |
1. Introdução
Propõe-se nesse artigo identificar obstáculos que contribuem com a elevação do índice de reprovação e/ou evasão dos discentes na disciplina de cálculo I dos cursos de engenharia, e a partir da análise da pesquisa tem-se por objetivo principal buscar respostas para as causas dessas reprovações e/ou evasão, uma vez que ao ingressar no curso superior seja para obter o status de universitário ou para oportunizar-se a um emprego e consequentemente a uma vida melhor, não se tem a meta de um prolongamento da escolaridade ou até de um fracasso escolar.
Os altos índices de não-aprovação nas disciplinas de cálculo que prejudicam o rendimento dos estudantes atrasando o seu curso universitário, têm sido foco de diversas pesquisas que detectaram possíveis causas para as dificuldades na aprendizagem.
Segundo Van Zanten (1999, p.51) apud ZAGO (2006) mudanças no campo da sociologia com a recomposição da problemática das desigualdades de escolarização entre classes sociais envolvendo, entre outras questões, as estratégias familiares de escolarização, as variações nas configurações escolares entre grupos sociais e no interior de um mesmo grupo; o ensino instrucionista e a dificuldade para relacionar a teoria e a prática na abstração tanto no raciocínio lógico-dedutivo quanto na análise de gráficos e suas demonstrações provenientes da falta de experiências prévias juntamente com a desmotivação por acreditar ser essa disciplina um obstáculo difícil de ser superado.
2. Fundamentação Teórica
2.1 Não aprovação e evasão
De acordo com Bardagi e Hutz (2009) pesquisas revelam o aumento de ingressantes, porém o abandono ou trancamento de matrículas nas universidades é também um fenômeno em expansão. Apesar da intensificação das pesquisas acerca do tema a partir de 1995, com a criação da Comissão Especial de Estudos sobre Evasão, através da Portaria Secretaria de Educação Superior/Ministério da Educação - SESu/MEC, indicando uma valorização, é um assunto ainda pouco explorado.
Define-se evasão de curso como a saída do aluno de seu curso de origem, sem concluí-lo. Os índices de evasão costumam variar, em instituições públicas ou privadas, entre 20% e 50% De acordo com Ghizoni e Teles (2005); Mazzetto e Carneiro (2002); MEC (2002); Mercuri e Polydoro (2004) e Palma (2005) apud Bardagi e Hutz (2009). A não-aprovação e o desligamento costumam ser maiores nos anos iniciais do curso. Nesta linha, escrevem Bardagi e Hutz (2009), os alunos acabam por considerar natural um insucesso nas disciplinas de exatas, e os professores estabelecem padrões de reprovação "normais". É importante ressaltar que a não-aprovação é um aspecto substancialmente negligenciado pelas universidades e que tem sido quase totalmente atribuído aos alunos, ao invés de ser visto como um problema da instituição como um todo.
Os índices de reprovação no curso de engenharia, nas disciplinas de cálculo são, em geral, muito altos, prejudicando o rendimento dos estudantes e atrasando seu curso universitário. Rezende (2003) e Barufi (1999) estão entre os pesquisadores brasileiros que se preocupam com o baixo desempenho dos alunos em cálculo, mas isso não é prerrogativa só dos universitários brasileiros: há uma preocupação mundial com o fracasso em cálculo, que deu origem ao movimento conhecido como calculus reform, na década de 80.
Segundo seus precursores, o calculus reform tem como características básicas: o uso de tecnologia, isto é, software computacional e calculadoras gráficas, tanto para o aprendizado de conceitos e teoremas como para a resolução de problemas; o ensino via a "Regra dos Três", isto é, todos os tópicos e todos os problemas devem ser abordados numérica, geométrica e analiticamente; grande preocupação, ou pretensão, em mostrar a aplicabilidade do Cálculo através de exemplos reais e com dados referenciados; tendência a exigir pouca competência algébrica por parte dos alunos. (REZENDE, 2003, p.3).
As pesquisas relacionadas ao fracasso em cálculo focam principalmente as dificuldades da compreensão das noções de função, limite e derivada, no domínio do Teorema Fundamental do Cálculo, ou na forma como os alunos estudam (NASSER, 2008).
No ensino médio, em geral, os alunos são acostumados a resolver mecanicamente os exercícios, decorando regras e macetes, não sendo estimulados a raciocinar. No início do curso superior, segundo Zendron (2007) apud Araújo et al. (2011), os alunos se deparam com exigências que não estão prontos para enfrentar, pois não tiveram oportunidade de desenvolver habilidades de argumentação e o ensino no curso de engenharia tem seguido predominante a tendência da pedagogia tradicional, onde a compreensão e assimilação de matérias passadas pelos professores em sala de aula é o produto desta educação. Um dos motivos que fazem com que a pedagogia tradicional ainda prevaleça, é o fato de grande parte dos professores que lecionam nesse curso, ser formado de acordo com este modelo educacional. Dessa forma, estes docentes acreditam na eficácia do seu método para garantir, ao seu aluno, o aprendizado esperado. Contempla Gomes:
Ministrada no início do curso, [Cálculo I] passa a ser o primeiro contato, para o aluno, com uma Matemática "diferente" daquela que trabalhava no Ensino Médio. Somada às novidades do ser universitário, muitas vezes, a imaturidade e as algumas deficiências trazidas do processo educacional anterior, a reprovação e evasão no primeiro período dos cursos de Engenharia não é novidade. (GOMES, 2012, p.1)
O processo de aprendizado de conteúdos complexos, como os de cálculo I, exige fundamentalmente o domínio de uma série de conhecimentos básicos. No ensino superior, entretanto, parte-se do falso pressuposto de que, se passou no vestibular, o aluno tem todos os pré-requisitos necessários para a disciplina, critíca Gomes (2012). Outra marca do pensamento pedagógico tradicional é a crença equivocada de que o aluno já chega pronto à universidade. Contudo, um olhar sobre o nível de conhecimento matemático dos calouros indicaria que uma parcela detém o domínio, outra apresenta uma série de deficiências e outra sequer tem o mínimo necessário para frequentar as aulas.
Para Loder (2002) a educação precisa proporcionar uma experiência de aprendizagem e não somente a questão dos conhecimentos prontos e, mesmo sendo comum, no curso de engenharia: mudanças da grade curricular dos cursos, aumento ou redução da carga horária das disciplinas, reflexão sobre estágios obrigatórios e de projetos de final de curso; são deixadas de lado as pedagogias em ação, os processos de aprendizagem e a formação do futuro engenheiro. Isso acontece, talvez, pela ausência de repensar o papel deste engenheiro-professor.
É preciso salientar a importância de um projeto pedagógico comprometido com a realidade, que respeite o aluno oferecendo condições de enfrentamento de possíveis problemas de natureza pedagógica ou de natureza comportamental e os próprios componentes do sistema de ensino e aprendizagem desta disciplina: coordenadores, professores e alunos, deverão perceber como errônea a concepção da banalização do processo de ensino e aprendizagem.
Para que a qualidade de ensino seja alcançada plenamente é necessário abrir espaço para discutir a própria sala de aula, ambiente onde professor e aluno deverão desenvolver suas potencialidades e buscar estratégias inovadoras de ensino que resultarão na aprendizagem esperada. O professor precisa ser formado para interagir com os alunos reais; não se pode compactuar com a ideia de que o professor estabeleça, a priori, o que os alunos deveriam saber ou ter condições de fazer.
Grande parte das dificuldades enfrentadas por alunos são, a rigor, criadas pelos próprios professores. Muitas vezes a linguagem que os professores utilizam é distante da realidade dos alunos como afirmam Souza et al. (2009), e quando o educador se limita a simplesmente ler e resolver mecanicamente o que está proposto no material didático, por ser menos trabalhoso, ainda mais num país como o Brasil, onde as diferenças regionais são enormes e o material didático é apenas um, aumenta a dificuldade de compreensão e relação teoria e prática do conteúdo.
Segundo Denoti (2005) apud Araújo et al. (2011) é por meio da matemática que se elucidam os diversos conceitos usados na engenharia, porém, no entanto, tal ensino, nesses cursos, vem sendo vivenciado de forma a instalar sentimentos como passividade, insegurança e dependência aos alunos, em razão da forma para se chegar a uma resolução matemática, optando por modelos de resolução prontos. Outra situação muito problemática e comum às salas de aula é o fato da superlotação, onde as dificuldades individuais nem são percebidas e o conteúdo tem de ser vencido a qualquer custo.
2.2 Projeto de experimentos
O projeto de experimentos (comumente chamado de DOE, do inglês design of experiments) é uma abordagem utilizada para a identificação dos fatores que mais contribuem com o desempenho de um produto ou de um processo. Para Rotondaro (2002), um projeto de experimentos consiste de uma série de testes conduzidos de forma planejada, em que as entradas (ou fatores controlados) são alteradas de modo planejado para avaliar seu efeito sobre uma saída (ou variável resposta). Moen et al (2012) mencionam que um experimento é um estudo analítico empreendido para fornecer uma base para a ação.
Um experimento do tipo fatorial completo 2k permite a determinação do efeito de todos os k fatores envolvidos e o efeito das interações (combinações) entre eles, considerando uma variação em dois níveis, para cada fator (MONTGOMERY, 2004).
Para identificação e análise dos efeitos de cada fator e das suas interações sobre a variável resposta de interesse, algumas formas gráficas são utilizadas. Montgomery (2004) utiliza-se das seguintes representações gráficas (Quadro 1), para apresentação dos resultados dos experimentos.
Quadro 1 – Representações gráficas e suas funções
Representação Gráfica |
Função |
Geograma (quadrado) ou Diagrama do cubo. |
Para mostrar o efeito dos fatores em seus níveis, sobre a váriável resposta. São utilizados geogramas especificamente para experimentos envolvendo dois fatores. São utilizados cubos especificamente para experimentos envolvendo três fatores. |
Gráfico de probabilidade normal dos efeitos. |
Para mostrar qual dos fatores ou interações geradas no experimento tem maior significância sobre a variável resposta. |
Gráfico de probabilidade normal dos resíduos. |
Para confirmar a consistência estatística do modelo utilizado. Visam mostrar a normalidade e a independência (aleatoriedade) dos dados. |
Gráfico dos efeitos principais |
Para mostrar como a variável resposta se comporta na mudança de um nível para outro de cada fator. |
Gráfico das interações |
Para mostrar se existe interação entre fatores e o comportamento da variável resposta na mudança de níveis. |
Fonte: Adaptado de: SANTOS, 2013.
Quando o número de fatores a avaliar for muito alto, como acontece algumas vezes no início do procedimento de experimentação, é recomendado que sejam conduzidos anteriormente, experimentos fatoriais fracionados (uma fração de um experimento fatorial completo) para aumentar o nível de conhecimento do objeto de estudo, com uma quantidade menor de ensaios a realizar (WERKEMA, 1996).
Uma das abordagens de realização do projeto e análise de experimentos, mais utilizada atualmente, é a proposta por Montgomery (2004), que apresenta uma sequência de algumas etapas que devem ser observadas pelos envolvidos no planejamento e execução de um projeto de experimentos:
- Reconhecimento e relato do problema;
- Escolha dos fatores e dos níveis;
- Seleção da variável resposta;
- Escolha do planejamento experimental;
- Realização do experimento;
- Análise dos dados.
A observância da realização criteriosa dessas etapas é fundamental para a obtenção de dados válidos, interpretação dos resultados e entendimento das mudanças a serem implementadas. Porém podem ser encontradas diferentes abordagens para a realização de projetos e análise de experimentos que apresentam visões distintas para a condução e análise experimental como os estudos de Fisher, Plackett e Burman, George Box, Genichi Taguchi e Dorian Shainin apud Santos (2013).
3. Procedimento Metodológico
O propósito deste trabalho é evidenciar os motivos que levam os ingressantes de um curso superior de engenharia, a não obterem a aprovação numa disciplina, fato que pode prolongar o prazo de conclusão do curso, ou, até mesmo, provocar a evasão dos estudantes do curso.
Para analisar estas questões foi realizado um levantamento de informações diretamente com os graduandos de engenharia de uma instituição de ensino superior localizada na região sul do Brasil, no início do 2º semestre de 2013, em busca de um maior entendimento de suas dificuldades bem como dos fatores que podem levar a uma não aprovação. Os sujeitos da amostra são estudantes de cálculo I, de duas turmas de um curso de engenharia que frequentaram as aulas em dois turnos diferentes (matutino e noturno) num mesmo semestre. A disciplina de cálculo I compreende o estudo de funções, limites e derivadas.
Nesse sentido buscou-se aplicar, como metodologia de trabalho, as etapas sugeridas por Montgomery (2004) para a realização de um experimento estatisticamente planejado.
4. Análise Estatística da Não Aprovação dos Estudantes
A abordagem de Montgomery foi utilizada nesta pesquisa visando aumentar a chance de sucesso na análise dos dados e diagnóstico do processo. Com esse intuito é fundamental ter-se uma ideia clara do objetivo do experimento, de que fatores exatamente devem ser estudados, de como o experimento deve ser conduzido e uma noção de como os dados serão analisados.
4.1 Reconhecimento e relato do problema
A não aprovação e/ ou evasão dos discentes já no primeiro ano do curso de engenharia, na disciplina de cálculo é uma realidade e tem sido fator importante percebido com preocupação pelos docentes e outros profissionais envolvidos na área educacional. Este cenário motivou a formatação desta pesquisa.
O objetivo deste experimento foi identificar os fatores que mais prejudicam o desempenho dos discentes, bem como, compreender o modo com que estes influenciam o aprendizado.
4.2 Escolha dos fatores e dos níveis
Mediante brainstorming realizado durante reuniões com professores destas turmas, foram elencados alguns fatores a serem analisados com a aplicação da técnica estatística de planejamento de experimentos. Para cada fator escolhido como significativo, com base na experiência dos professores, foram selecionados dois níveis de variação. Os fatores escolhidos e seus respectivos níveis são apresentados a seguir:
- Escola: o fator escola foi selecionado com a intenção de identificar junto aos graduandos se o ensino médio havia sido realizado em uma escola pública ou privada. Considerou-se escola pública um dos níveis de variação e escola privada o outro nível de variação, para este fator.
- Turno: outro critério para analisar as diferenças de rendimento na disciplina de cálculo I foi o horário de realização das aulas; utilizou-se neste caso o fator turno de estudo, variando entre os níveis matutino e noturno.
- Afastamento: o tempo de afastamento dos estudos pelo educando entre o ensino médio e a graduação, segundo os professores, também poderia estar colaborando com o aumento das dificuldades. Para medir o efeito do fator afastamento, levou-se em consideração os níveis "mais de três anos" e "menos de três anos" de afastamento.
- Atividade: o fator atividade foi selecionado também, visando avaliar o efeito de um grupo de estudantes que somente estudam, de outro grupo de estudantes que além de estudar também trabalham (tem outra atividade) em outra organização.
4.3 Seleção da variável resposta
Entre os maiores problemas que os sujeitos estudados enfrentam estão a qualidade da educação básica, as diferenças metodológicas do ensino médio e do superior, as dificuldades intrínsecas das matérias, o tempo que o estudante dedica ao estudo (disponibilidade extraclasse) e a distância temporal entre o final do ensino médio e o ingresso no curso superior. Este conjunto de fatores tem gerado um alto índice de não-aprovação na disciplina. Assim optou-se por selecionar como variável resposta o número de "não-aprovações".
4.4 Escolha do planejamento experimental
Para análise dos dados obtidos junto aos estudantes, foi utilizada a técnica estatística de planejamento experimental (DOE – design of experiments), com auxílio do software estatístico Minitab®, versão 16. Por meio dele, é possível planejar e conduzir o experimento de acordo com a técnica escolhida e avaliar, de forma gráfica, quais os fatores cujos efeitos são mais significativos e os níveis ideais para uma resposta melhor. Este tipo de planejamento experimental é adequado para estudar, de forma eficiente e econômica, o efeito conjunto de vários fatores sobre uma variável tornando as respostas mais visíveis.
Optou-se por realizar um experimento fatorial completo do tipo 24 (com quatro fatores em dois níveis). Com o auxilio do software Minitab ® foi elaborada uma matriz que contempla todas as combinações possíveis entre os fatores selecionados e seus níveis de variação, conforme planejamento experimental escolhido (tabela 1).
Tabela 1- Matriz com as combinações possíveis.
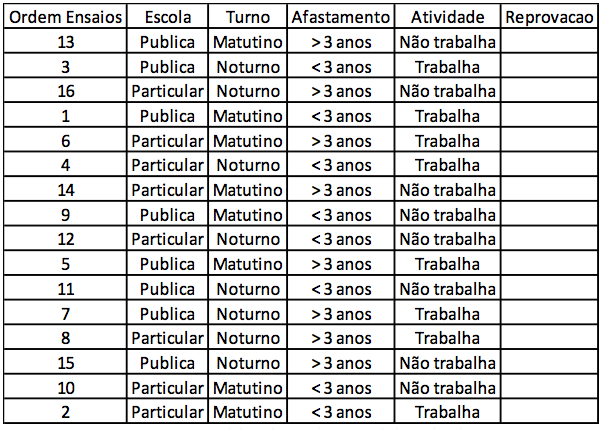
Fonte: elaborado com base nos dados coletados.
É importante observar que o software aleatoriza (sorteia) a sequência de realização dos 16 ensaios previstos neste experimento. Essa é uma medida que provê qualidade estatística aos resultados obtidos, minimizando o erro experimental.
4.5 Realização do experimento
De posse da matriz e de um questionário, a pesquisadora realizou em sala de aula uma entrevista com os alunos das duas turmas para coletar os dados necessários ao seu preenchimento. Ao final do semestre as informações obtidas foram tabuladas, permitindo o preenchimento dos dados relativos a variável resposta, conforme mostra a tabela 2.
Tabela 2 – Tabela para análise dos resultados.
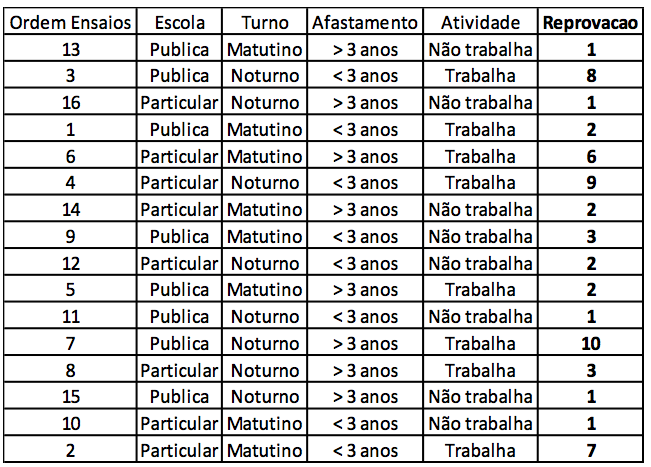
Fonte: elaborado com base nos dados coletados.
Os valores registrados na coluna "reprovação" refletem o comportamento observado no período de acompanhamento das turmas (6 meses de dedicação dos estudantes na disciplina de cálculo I)
4.6 Análise dos dados
Com o auxílio do software estatístico Minitab ® fez-se inicialmente uma análise dos efeitos dos fatores sobre a variável resposta (número de reprovações). O gráfico de Pareto dos efeitos, gerado pelo Minitab ®, mostrou que o efeito mais significativo estava relacionado ao fator atividade, conforme mostra a figura 1.
Figura 1 – Gráfico dos efeitos.
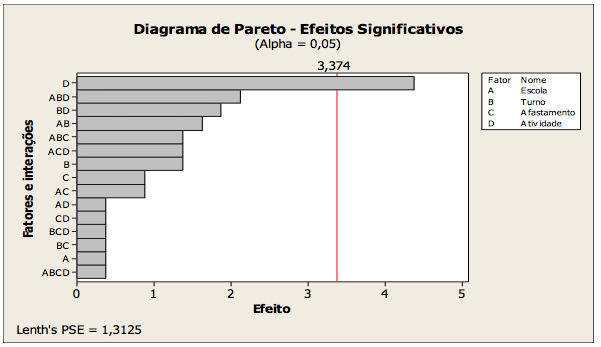
Fonte: elaborado com base nos dados coletados.
A figura 1 mostra também que o efeito dos outros fatores e de suas interações, tem pouca significância sobre a variável resposta. A leitura deste gráfico possibilitou então a visualização do fator mais significativo para a "não aprovação na disciplina de cálculo", conforme dados coletados junto às turmas.
De acordo com o gráfico da figura 2, também gerado pelo software Minitab ®, constatou-se que os estudantes que desenvolvem atividades laborais simultaneamente aos estudos, apresentam um maior número de não aprovações.
Figura 2 – Gráfico do efeito do fator atividade.
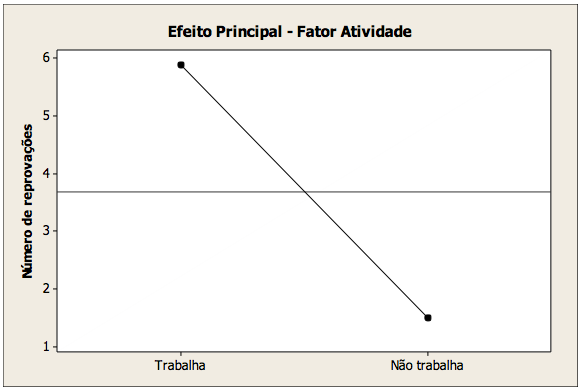
Fonte: elaborado com base nos dados coletados.
Neste gráfico (figura 2) é possível perceber um aumento de aproximadamente cinco pontos no número de não-aprovações em relação aos alunos que não trabalham.
A partir das observações dos índices obtidos pelo traçado dos gráficos percebe-se que o maior obstáculo/ fator identificado como prejudicial ao desempenho dos discentes causando a não aprovação foi a atividade, ou seja, além de estudar ele também trabalha, pois sustenta ou precisa auxiliar no sustento da casa e o estudo passa a não ser a primeira opção. Outro problema enfrentado pelos alunos em questão reside em advirem de um contexto educacional deficiente na qualidade do ensino público e encontram então dificuldades para prosseguir sua escolaridade, uma vez que os conteúdos da graduação exigem conhecimento prévio e fundamentalmente o domínio de uma série de conhecimentos básicos.
5. Conclusão
O instrumento investigativo (questionário) permitiu a tabulação dos dados de maneira a facilitar o entendimento da resposta, o que servirá como subsídio para a sugestão de melhorias. Dessa forma as disciplinas básicas dos cursos de engenharia precisam ser organizadas com o propósito de capacitar os aprendizes no desenvolvimento do raciocínio dedutivo, proporcionando-lhes uma visão do relacionamento dos conceitos matemáticos com situações reais.
O artigo mostrou que outros fatores também prejudicam o rendimento dos estudantes, porém com menos intensidade, podendo também atrasar a conclusão do seu curso universitário.
As causas aqui detectadas não esgotam o assunto. Constatou-se que o desenvolvimento de uma atividade laboral de forma simultânea com atividade acadêmica, é o fator que está mais influenciando o desempenho insatisfatório do grupo de estudantes pesquisado. É importante salientar que este resultado não pode ser generalizado para outros grupos expostos a outras realidades, por se tratar de um caso de amostragem não probabilística.
A busca de um ambiente educacional que oportunize o amadurecimento, equilíbrio e a aprendizagem deve ser uma constante. Entende-se que através deste tipo de diagnóstico é possível estimular o debate e proposta de soluções para o problema. Criar estratégias e intervenções que contribuam para desenvolvimento de aprendizagem significativa, levando os alunos a usarem o conhecimento matemático para perceberem a realidade sob diferentes pontos de vista e a proporem formas alternativas de resolver os problemas com os quais lidam.
Referências
ARAÚJO, P.; et al. (2011); Reprovação nas disciplinas básicas: uma reflexão dos aspectos pedagógicos, na perspectiva dos docentes e discentes aprovados. Anais: XXXIX - Congresso Brasileiro de Educação em Engenharia. Curitiba: ABENGE, URPR, PUCPR, UTPR.
BARUFI, M. C. B. (1999); A construção/negociação de significados no curso universitário inicial de Cálculo Diferencial e Integral. Tese de Doutorado – Faculdade de Educação, Universidade de São Paulo.
GOMES, E. (2012); Ensino e aprendizagem do cálculo na engenharia: um mapeamento das publicações nos COBENGEs. In: XVI Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática, Canoas: ULBRA.
BARDAGI, P. M.; HUTZ, C. S. (2009); Não havia outra saída: percepções de alunos evadidos sobre o abandono do curso superior. Psico-USF (Impr.) vol.14 no.1 Itatiba.
LODER, L. L. (2002); Epistemologia versus pedagogia: o locus do professor de engenharia - Dissertação de Mestrado defendida junto ao programa de Pós-Graduação em Educação da UFRGS – PPGEDU/UFRGS.
MINITAB ® Statistical Software, version 16. State College, Pensilvânia: Minitab Inc, 2010.
MOEN, Ronald D.; Nolan, Thomas W.; Provost, Lloyd P. (2012) Improving Quality Through Planned Experimentation. New York: McGraw-Hill Inc.
MONTGOMERY, D. C. (2004); Controle estatístico da qualidade. Rio de Janeiro: LTC - Livros Técnicos e Científicos Editora S/A.
NASSER, L. (2008); Ajudando a superar obstáculos na aprendizagem de cálculo. Universidade Federal do Rio de Janeiro.
REZENDE, W. M. (2003); O Ensino de Cálculo: dificuldades de natureza epistemológica. Universidade de São Paulo Faculdade de Educação.
ROTONDARO, R. G. (2002); Seis sigma: estratégia gerencial para a melhoria de processos, produtos e serviços. São Paulo: Atlas.
SANTOS, A. J.; JUNCKES, R. S. (2013); O ensino de projeto de experimentos em cursos de tecnologia e engenharia: análise crítica de recursos pedagógicos disponíveis. Joinville, SC: Sociedade Educacional de Santa Catarina – SOCIESC.
SOUZA, A. A. et al. (2009); Dificuldades no aprendizado de cálculo diferencial e integral nas licenciaturas da área de ciências. Ceará.
ZAGO, N. (2006); Do acesso à permanência no ensino superior: percursos de estudantes universitários de camadas populares. Publicado revista Brasileira de Educação. Universidade Federal de Santa Catarina, Programa de Pós-Graduação em Educação.
1. Programa de Mestrado Profissional em Engenharia de Produção, Centro Universitário Tupy – UniSociesc, Joinville, Brasil) . Email: renata.feuser@gmail.com
2. Programa de Mestrado Profissional em Engenharia de Produção, Centro Universitário Tupy – UniSociesc, Joinville, Brasil). Email: antoniodos.santos@bol.com.br