Espacios. Vol. 35 (Nº 12) Año 2014. Pág. 19

Descoberta de conhecimento em bases de dados no processo de produção de alumina

Knowledge discovery in databases in the production process of alumina

Carla Regina Mazia ROSA 1, Cleina Yayoe OKOSHI 2; Maria Teresina Arns STEINER 3; Ruy Gomes da SILVA 4; Wesley Vieira da SILVA 5.

Recibido: 12/08/14 • Aprobado: 24/10/14

Contenido

1. Introdução

2. Descrição do problema

3. KDD e DATA MINING

4. Metodologia

5. Obtenção dos resultados

6. Conclusão

Referências bibliográficas

1. Introdução

A produção mineral se caracteriza por sua relevância no contexto econômico, podendo ser considerada uma das atividades mais impactantes ao solo, embora, em geral, não afete amplas extensões territoriais. Aproximadamente 7% da crosta terrestre é composta por alumínio, fazendo deste elemento químico o terceiro mais abundante na Terra, depois do oxigênio e do silício. A produção de alumínio começa com a matéria-prima bauxita. A mineração de bauxita, por sua vez, caracteriza-se pela retirada da vegetação, seguida de intensa movimentação das camadas superficiais do solo e a consequente geração de rejeitos e, por este motivo, é considerada uma atividade de alto impacto ambiental.

O alumínio para ser produzido necessita de alumina, que é extraída da bauxita por meio de um processo químico composto por várias etapas de transformações, até atingir o estado de alumina. O processo mais utilizado industrialmente é o Processo Bayer, que consiste em misturar a bauxita moída a uma solução de soda cáustica, com a qual a mesma reage sob pressão e temperatura, dissolvendo a bauxita e formando uma solução de aluminato de sódio (Luz, Lins, 2005), chamada de rejeito.

O rejeito de um processo de produção de alumina, conhecido como lama vermelha, fica depositada em bacias expostas ao meio ambiente, podendo danificá-lo e, por este motivo, é desejável que tais teores sejam minimizados.

O processo de Descoberta de Conhecimento em Bases de Dados (Knowledge Discovery in Database – KDD) tem se mostrado efetivo na gestão de informações, do qual a Mineração de Dados (Data Mining – DM) é a sua principal etapa.

Segundo Cardoso e Machado (2008), o DM é capaz de revelar, automaticamente, o conhecimento que está implícito em grande quantidade de informações armazenadas nos bancos de dados de uma organização. As técnicas de DM podem fazer uma análise antecipada dos eventos, possibilitando prever tendências e comportamentos futuros, permitindo aos gestores a tomada de decisões baseada em fatos e não em suposições.

Dentre os métodos de DM, capazes de fazer o re­conhecimento de padrões, têm-se os métodos estatísticos, dentre os quais se destacam a Regressão Logística Binária (RLB), as Redes Neurais, as Máquinas de Vetores de Suporte (Support Vector Machines - SVM) e as meta-heurísticas de uma forma geral, resultando em funções que estimem o comportamento de um conjunto de dados, buscando a maximização de sua eficiência.

Assim sendo, o presente trabalho tem por objetivo discriminar os dados relativos aos teores de soda cáustica contidos na lama vermelha (padrões), para que obtidos novos padrões, sua classificação possa ser realizada com o menor erro possível tendo-se, assim, condições de antecipar ações que possam minimizar o teor de soda cáustica contida na lama vermelha. Para isso, pretende-se aplicar o processo KDD com a técnica de RLB na etapa de DM.

O presente artigo está organizado em seis seções. Além desta seção introdutória tem-se na seção 2 a descrição do problema aqui abordado. A seção 3 comtempla a revisão da literatura a respeito do processo KDD e da técnica de DM, a RLB. A seção 4 apresenta a metodologia, ou seja, como o problema será abordado. Na seção 5 tem-se a obtenção dos resultados, tanto da análise exploratória dos dados, quanto da RLB. Para a utilização da RLB, são propostos dois testes com o intuito de se obter resultados com a máxima acurácia. Finalmente, na seção 6 são apresentadas as considerações finais.

2. Descrição do problema

Atualmente, o mercado mundial possui 46 países produtores de alumínio, onde o Brasil ocupa o sexto lugar, com a terceira maior reserva do minério (bauxita), localizada na região amazônica e em reservas que podem ser encontradas no sudeste do Brasil, na região de Poços de Caldas e Goitacazes, MG (Abal, 2013). Porém nem toda a bauxita processada gera alumina, pois existe um grande percentual de rejeito do processo não aproveitável economicamente. A quantidade de rejeito depende da qualidade da bauxita, que influencia diretamente na quantidade de lama vermelha gerada.

Há uma relação de produtividade existente na produção da alumina, sendo que cada tonelada de alumina produzida, necessita de duas toneladas de bauxita que, conforme já comentado, varia de acordo com a especificação de cada tipo de bauxita. Cada tonelada de bauxita contém um percentual de alumina aproveitável de 50%, sendo que o restante é composto por silicatos, ferro, manganês, potássio e outros metais não economicamente exploráveis (a lama vermelha).

O fato é que a quantidade de lama vermelha gerada anualmente tem assumido enorme proporção, da ordem de milhões de toneladas, representando um sério risco ao meio ambiente. Além disso, junto com a lama vermelha perde-se uma quantidade considerável de soda cáustica, o que também contribui significativamente nos custos de reposição desse insumo, já que é um dos principais insumos e de maior custo na produção da alumina.

O controle de teor cáustico no rejeito do processo de alumina é um dos desafios enfrentados pelas empresas deste ramo, que está diretamente ligado ao controle ambiental da organização. A soda cáustica é um dos principais insumos no processo de produção da alumina, que é matéria prima na produção do alumínio.

A necessidade de um controle efetivo do teor cáustico auxilia não somente na redução de custos da organização, pois cada tonelada de soda cáustica que fica retida no rejeito necessita ser reposta no processo, a qual tem um elevado custo de aquisição, como também reduz os impactos ambientais causados pelo produto químico. Com a redução deste teor cáustico na lama vermelha haverá a possibilidade desta ser utilizada na fabricação de cerâmicas e na construção civil, já que poderá fazer parte da composição do concreto.

O alumínio é um metal extremamente importância no segmento industrial, o que torna seu consumo cada vez maior, através da descoberta de novas ligas metálicas, as quais possibilitam a sua aplicação nos mais variados segmentos industriais e atividades em geral, sejam de natureza econômica ou de uso doméstico. Ele é produzido em escala comercial desde o século XVIII e seu mercado vem se expandindo desde então.

Segundo Luz (2003), a produção anual de bauxita é superior a 120 milhões de toneladas, onde cerca de 95% da produção são utilizados na obtenção do alumínio metalúrgico, pelo Processo Bayer, seguido do processo Hall-Héroult, cujo produto final é o metal, ou seja, o alumínio têm produção estimada em 40 milhões de toneladas por ano. Uma pequena percentagem de bauxita (5%) não-metalúrgica após calcinação é aplicada na manufatura de abrasivos, refratários, cimento, entre outras.

A alumina utilizada para produtos químicos, não é calcinada, mantendo-se na forma hidratada. De acordo com o International Aluminium Institute (Iai, 2013) aproximadamente 40% da produção de bauxita produzida no mundo provêm da Austrália, destacando-se, ainda como principais produtores: Guiana (14%), Jamaica (11%), Brasil (8%), Índia (5%) China (3%). As reservas mundiais de bauxitas estão distribuídas nas regiões tropicais (57%), mediterrânea (33%) e subtropicais (10%).

O principal processo de extração de Alumina da bauxita foi desenvolvido em 1858 por Le Chatelier e aperfeiçoado posteriormente em 1888 por Karl Bayer, sendo conhecido atualmente como processo Bayer (Hind et al. 1999).

O Processo Bayer extrai a alumina que está contida na bauxita, quando dissolvida em solução de soda cáustica sob determinadas condições de pressão e temperatura. O processo apresenta uma melhor extração, dependendo da natureza do minério de bauxita, devido suas diferentes características químicas. Deste modo, mesmo que diferentes empresas utilizem o mesmo processo de extração, acabam obtendo diferentes valores de concentração de soda cáustica no rejeito, devido a melhorias tecnológicas implementadas por cada unidade fabril. Estima-se um valor de 15g/l de soda cáustica para cada tonelada de rejeito gerado sendo que, atualmente, este material é acondicionado em bacias próprias expostas ao meio ambiente.

Tal valor é considerado elevado, pois a soda cáustica é um contaminante. Um resultado ideal seria um valor nulo de soda cáustica na lama, porém tal valor é inviável para o processo devido seu alto custo operacional. Dependendo dos distúrbios do processo, este valor poderá chegar em 40 g/l, que além de aumentar a contaminação da lama vermelha, eleva os custos de produção, tendo-se em vista que esta soda cáustica necessitará ser reposta no processo. Desta maneira, a lama vermelha foi considerada um resíduo inaproveitável para a indústria do alumínio (Chaves, 1962).

McLellan et al. (2009) afirmam que existem avanços na busca do alinhamento da indústria mineral e o compromisso com o desenvolvimento sustentável, através da redução do impacto ocorrido pelo processo produtivo. Segundo Hilson e Murck (2000), esta integração requer um compromisso de melhoria ambiental e socioeconômica contínua, desde a exploração mineral, passando pela operação, até o fim da cadeia.

As variáveis independentes utilizadas nesse estudo foram em um total de nove: Vazão, Densidade, Injeção, Vácuo, Nível da bacia, Rotação, Spray, TTS (teor total de soda), Soda na lama (nível de soda cáustica na lama vermelha) e uma variável dependente (resposta), Concentração (teor final de soda cáustica). Foram coletadas 1060 observações (quantidade de padrões; amostras), das quais 669 foram consideradas como sendo de boa qualidade (teor de soda cáustica < 12; Classe "Bom") e 391 foram consideradas como sendo de baixa qualidade (teor de soda cáustica ≥ 12; Classe "Ruim"). O valor "12" foi definido pelos especialistas da área como sendo um "valor limite" para a discriminação de uma amostra da classe "Bom" ou da classe "Ruim". Na tabela 1, a seguir, são apresentados 20 dos 1060 dados, dos quais os 10 primeiros são da classe "Bom" e os 10 seguintes da classe "Ruim".

Tabela1 - Dados do processo de lavagem de lama

3. KDD e DATA MINING

A definição KDD foi dada por Fayyad et al. (1996) como sendo: "o processo não trivial de identificação de padrões válidos, novos, potencialmente úteis e compreensíveis, embutidos nos dados" e caracteristicamente composto das seguintes etapas: seleção dos dados, pré-processamento, limpeza e preparação dos dados; processamento, que trata da descoberta de padrões mediante algoritmos de Mineração; pós-processamento, que refina os resultados obtidos durante o processamento, seja compondo novos padrões ou avaliando seu interesse, e interpretação dos padrões extraídos, úteis para a extração de conhecimento, ou seja, para a "tradução" de dados brutos em informações relevantes. Estas etapas estão ilustradas na Figura 1 a seguir.

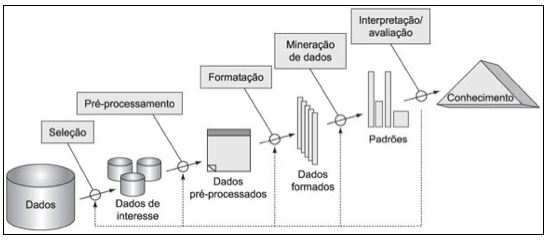
Figura 1. Etapas do Processo KDD. Fonte: Fayyad et al. (1996)

Segundo Tan et al. (2009) é importante não confundir os termos DM e KDD, visto que KDD é todo o processo até que se chegue ao resultado de um padrão de comportamento das variáveis ou relações. Já DM é considerada apenas uma das etapas, a mais importante, que compõem o KDD. O DM consiste da obtenção de padrões para a geração de conhecimento (Fayyad et al. 1996).

O DM é uma área emergente dentro da inteligência computacional usada na análise de grandes bancos de dados (Kusiak et al. 2000), com a geração de padrões e a extração de informações dessas bases (Mcdonald et al. 1998). Permite, por exemplo, examinar as relações de similaridade entre as informações (Linares, 2003).

Desta forma, o DM consiste da utilização de técnicas de Reconhecimento de Padrões (RP), aprendizado de máquina e estatística, seja para a classificação, predição, agrupamento ou associação de padrões. As técnicas são concebidas para agir sobre grandes bancos de dados, com o intuito de descobrir padrões úteis e recentes que poderiam de outra forma, permanecer ignorados. Estas técnicas vão desde as tradicionais da estatística multivariada, como análise de agrupamentos e regressões, até modelos mais atuais de aprendizagem, como redes neurais, lógica difusa e algoritmos genéticos.

3.1. Regressão logistica

Segundo Hines (2003), a estatística trabalha com a coleta, apresentação, análise e uso de dados para resolução de problemas, tomada de decisões, desenvolvimento de estimativas e planejamento tanto de produtos quanto de procedimentos, e ainda é usada para a descrição e a compreensão da variabilidade. Desta forma, um importante instrumento na estatística é a análise multivariada, que trata todas as variáveis simultaneamente, sumariando os dados e revelando a sua estrutura com a menor perda de informações possível (Gauch, 1982; Pielou, 1984).

Assim sendo, a Regressão Logística (RL) é definida como uma técnica estatística de análise multivariada que permite o ajuste de um conjunto de variáveis independentes a uma variável de resposta categórica. Ao contrário das variáveis contínuas, as variáveis categóricas podem assumir apenas alguns valores particulares de resposta, podendo estes ser binários (dicotômicos) cuja resposta possui apenas dois níveis (não ou sim) ou politômicos (mais de três classes), uma extensão do anterior, no qual a resposta pode assumir múltiplos níveis de saída (Hosmer, Lemeshow, 2000). A RLB consiste em relacionar, por meio de um modelo, a variável resposta (padrões pertencentes ao conjunto A ou B) com os atributos que influenciam em sua ocorrência (Hair et al. 2009).

As premissas básicas a serem atendidas são: a) a média condicional da equação da RL será um valor definido entre "0" e "1"; b) os erros da equação seguirão a distribuição binária; e c) os resultados obtidos podem ser entendidos na forma de probabilidades (Hosmer, Lemeshow, 2000).

O modelo de RL proposto por Hosmer e Lemeshow (2000), assume a relação exposta na equação (1), também conhecida como função logística.

onde:

 π (x) = representa a probabilidade associada a "x".

e = é o vetor de coeficientes a ser estimado caracterizado como um valor fixo, base dos logaritmos naturais (aproximadamente 2,718).

 = são os vetores das variáveis explicativas associadas ao evento.

pode ser linearizada pela transformação:

onde:

1-π(x) = representa a probabilidade de não ocorrer o evento.

 = representa a razão de probabilidades.

 = representa os coeficientes estimados

 x = representa as variáveis independentes.

A RLB é aplicada a uma variável dependente, sendo que esta variável não representa os valores dos dados brutos, mas representa a probabilidade do evento. Assim sendo temos para a RL a equação geral (3).

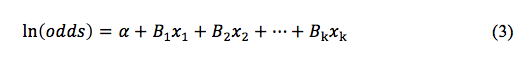
onde termos padrão das variáveis independentes estão representados a direita e a esquerda está o log natural da probabilidade e a quantidade ln(odds) é chamada de logit. Deste modo, retirando o problema de predição para fora dos limites da variável dependente. As probabilidades são relacionadas pela equação (4).

Na RL há um relacionamento linear com as variáveis independentes, mas é linear nas probabilidades de log e não nas probabilidades originais. Como o objeto de estudo é a probabilidade de ocorrência de um evento, a equação logística pode ser transformada numa equação na probabilidade (5) (Hair, 2009).

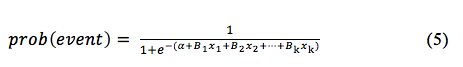
A regressão linear clássica, não segue uma distribuição normal, mas a de Bernoulli. De tal modo que na regressão linear o método usado para estimar os coeficientes β0, ..., βn é o método dos mínimos quadrados, e na RL usa-se o método da máxima verossimilhança, que maximizem a probabilidade de se obter o conjunto observado de dados (Hosmer, Lemeshow, 2000).

Desta forma, na RL minimiza o número de variáveis para que o modelo resultante seja mais facilmente generalizado e mais estável numericamente, dado que quanto mais variáveis são incluídas no modelo, mais ele se torna dependente dos dados. A técnica stepwise na RL é o processo de inclusão ou exclusão de variáveis do modelo, baseado em critérios tais com o teste Wald.

Para Crichton(2001), o teste Wald é utilizado para avaliar se o parâmetro é estatisticamente significativo, é obtido através da razão do coeficiente pelo seu respectivo erro padrão, e segue uma distribuição normal. A estatística de teste, para avaliar se o parâmetro β é igual a zero e pode-se especificar por meio da equação (6).

No entanto, o teste de Wald, falha quando se rejeita coeficientes que são estatisticamente significativos (Hauck, Donner, 1977). Assim sendo, recomenda-se que os coeficientes, identificados neste teste como sendo estatisticamente não significativos, sejam testados também pelo teste da razão de verossimilhança.

Após estimar os coeficientes da equação de regressão, é necessário verificar se cada variável é significantemente relacionada com a variável resposta do modelo, através dos testes de hipóteses estatísticas, que avaliam o modelo com a variável e sem a variável (Hosmer, Lemeshow, 2000). Desta forma o teste estatístico indica se houve ou não diferença estatisticamente significativa entre as classificações observadas e previstas.

Segundo Hair (2000), o ajuste geral do modelo pode ser avaliado utilizando-se algumas medidas como o -2LL. Contudo se ocorrer um decréscimo no valor -2LL comparado ao modelo base, existe melhora no modelo, pois o valor mínimo para -2LL é 0, o que corresponde ao ajuste perfeito. A medida R2 Cox e Snell opera da mesma forma, com valores mais altos indicando maior ajuste do modelo. Entretanto, esta medida está limitada pelo fato de que não consegue alcançar o valor máximo de 1, de modo que Nagelkerke propôs uma modificação que tem o alcance de 0 para 1. A terceira medida é a medida R2 "pseudo" com base na melhoria do valor –2LL. O pseudo R2 é calculado por meio da equação (7).

Para Hosmer e Lemeshow (2000) a medida final do ajuste do modelo mede a correspondência dos valores efetivos e previstos da variável dependente, que é indicado por uma diferença menor na classificação observada e prevista e ainda mostra a não significância, indicando a ausência de diferença na distribuição de valores. Um melhor ajuste de modelo é indicado por um valor chi-quadrado não significante. Por fim, as matrizes de classificação, idênticas em natureza às usadas na análise discriminante, demostram se as taxas de acerto são altas ou baixas para os casos corretamente classificados no modelo.

Desta forma, na RL deve necessariamente achar o modelo que melhor se ajuste aos dados em análise, com o intuito de conseguir um modelo moderado e razoável, que permita descrever a relação entre a variável resultado e um conjunto de variáveis independentes.

Mota (2007) apresenta uma proposta para a avaliação de imóveis urbanos (apartamentos, casas e terrenos) através de técnicas de análise multivariada e redes neurais artificiais. Steiner et al. (2008) utilizaram uma metodologia, composta por técnicas de análise multivariada, para a construção de um modelo estatístico de regressão linear múltipla para avaliação de imóveis em função de suas características.

Santos et al. (2007) analisaram a riqueza e similaridade florística de fragmentos florestais no Norte do estado de Minas Gerais, através do métodos de análise multivariada. Toledo et al. (2009) aplicaram análise multivariada para a caracterização fitossociológica em vegetação de Cerrado no Norte do estado de Minas Gerais. Outros estudos com abordagem em análise multivariada foram desenvolvidos por Oliveira-Filho, Fontes (2000) e Scudeller et al. (2001) na Mata Atlântica do Sudeste brasileiro.

4. Metodologia

A metodologia do trabalho foi dividida em duas fases, enquadradas no KDD. A 1ª. fase, a análise exploratória de dados, incorpora as três primeiras etapas do processo do KDD (Figura 1 já apresentada) , conforme a Figura 2 a seguir. A 2ª. fase contém a etapa de DM (RP)e interpretação dos resultados, conforme a Figura 2 a seguir.

 Figura 2. Fase do Processo.

Na 1ª. fase foi realizada a estatística descritiva dos dados e também o descarte de padrões atípicos. Com a estatística descritiva foi possível identificar os outliers, ou seja, que apresentavam características "fora do padrão".  Os outliers foram identificados pela análise dos escores padronizados (z). Esses outliers foram descartados, pois são considerados como padrões atípicos.

Na 2ª. fase foi aplicada a técnica utilizada de RL para a mineração dos dados, ou seja, para a classificação dos mesmos e, em seguida, foram obtidos e interpretados os seus resultados. Nessa 2ª. fase foram realizados dois testes: o primeiro, com a quantidade de padrões (observações da amostra) resultantes da 1ª. fase, ou seja, após a eliminação dos outliers e, em seguida, utilizada a ferramenta RL. O segundo teste foi realizado após a eliminação dos outliers, seguida da determinação do valor médio de uma das variáveis analisadas no estudo (variável "densidade"), conforme será mostrado mais adiante e, finalmente, foi plicada a RL.

5. Obtenção dos resultados

Os resultados foram obtidos por meio da aplicação das duas fases: análise exploratória e RL sobre os dados.

5.1. Análise exploratória de dados

Na análise exploratória de dados foram realizados a estatística descritiva dos dados e o descarte de padrões atípicos. Esta fase ocorreu com o auxílio do software SPSS 13.0. A estatística descritiva, apresentada na Tabela 2 a seguir, foi realizada com as 1060 (dados brutos) observações, das quais 669 pertencem à classe "Bom" e 391 à classe "Ruim".

Tabela 2- Estatística descritiva dos dados brutos  

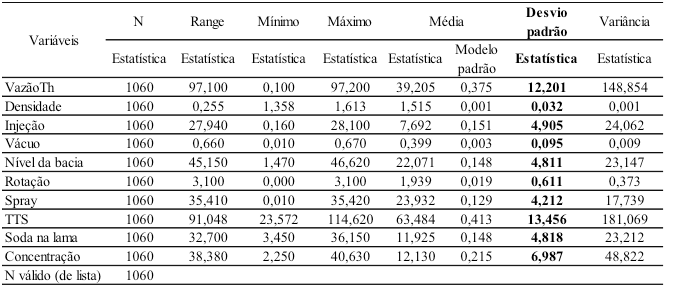
A Tabela 2 destaca que os desvios padrões da maioria das variáveis estão acima de "3", ou seja, apontando a existência de dados atípicos (outliers), que deverão ser excluídos, pois poderão influenciar negativamente, piorando o desempenho da RL, nos resultados da análise final. Dessa forma é fundamental identificar e excluir os outliers para que o resultado seja mais confiável.

Os outliers foram analisados através dos escores padronizados (z). Foram excluídos os dados que apresentaram z < -3 ou z > 3 para cada uma das variáveis analisadas individualmente. Desta forma, foram excluídas 82 observações (dados) e, portanto, a amostra ficou com 978 observações (624 da classe "Bom" e 354 da classe "Ruim"). A Tabela 3 apresenta a estatística descritiva com os dados após a exclusão dos outliers.

Tabela 3- Estatística descritiva após a exclusão dos dados atípicos (outliers)

Por meio da Tabela 3 é possível notar que os desvios padrões das variáveis, analisadas de forma conjunta, diminuíram após a exclusão dos 82 dados. Após a determinação da nova amostra foi realizada a 2ª. fase que descreve o processo para a utilização da técnica da RL.

5.2. Regressão logística

A técnica de DM, RL, foi aplicada por meio da realização de dois testes. Para o primeiro teste foi utilizada a amostra com 978 observações e o segundo teste utilizou uma nova amostra com 488 observações. As observações para o segundo teste foram formadas através da retirada de observações da primeira amostra por meio do valor médio da variável "densidade" (detalhado mais adiante); este segundo teste foi realizado, pois os resultados do primeiro teste foram insatisfatórios, ou seja, insuficientes para obter um desempenho aceitável da RL.

A. Primeiro teste

A técnica de RL foi aplicada às 978 observações obtidas após a 1ª fase (exlusão dos outliers), com o auxílio do software SPSS 13.0 utilizando o método stepwise foward, para definir o modelo final que minimiza o número de variáveis e maximiza a precisão do modelo.

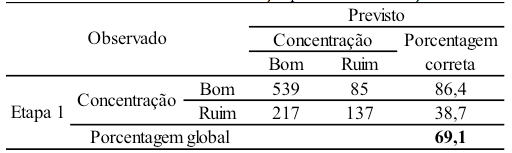
A Tabela 4, conhecida como "matriz de confusão", apresenta a classificação para as 978 observações. A taxa de acerto global foi de 69,1% e as taxas individuais de acertos foram: para a classe "Bom", de 86,4% e para a classe "Ruim", de 38,7%. Assim, dos 624 padrões da classe "Bom", apenas 85 estão na classificação de "Ruim" e dos 354 padrões considerados "Ruins" detinham 217 padrões "Bons". Ou seja, o resultado é considerado não tão satisfatório.

Tabela 4 – Tabela de classificação para as 978 observações

A Tabela 5 apresenta o resumo do modelo do primeiro teste, destacando os índices "R2 Cox e Snell" de 11,4% e "R2 Nagelkerke" de 15,7%. O "R2 Cox e Snell" indica que apenas 11,4% das variações ocorridas na RL são explicadas pelo conjunto das variáveis independentes, ou seja, este índice apresenta um baixo índice de explicação. O índice "R2 Nagelkerke" indica que 15,7% das variações registradas na variável dependente (Concentração) são ocasionadas pelas variáveis independentes. Ou seja, este índice também apresenta baixa explicação.

Tabela 5 – Resumo do modelo para as 978 observações

Por esse motivo foi realizado um novo teste que resultasse em melhoria da qualidade no reconhecimento dos padrões da amostra. Assim, para realizar o segundo teste analisou-se as variáveis que não detinham influência sobre o modelo do primeiro teste, como mostrado na Tabela 6.

Tabela 6 - Análise das variáveis não possuem influência no modelo de RL

A Tabela 6 apresenta todas as nove variáveis analisadas e seu nível de significância. Pode-se observar que existem 4 variáveis independentes (densidade, injeção, vácuo e nível da bacia) que não influenciam o modelo, pois o valor de p > 0,05 para todas elas. Como a "densidade" tem um nível de significância maior do que as demais três variáveis, os comportamentos dos dados dessa variável foram, então, melhor analisados.

O comportamento dos dados da variável independente "densidade" foi analisado por meio de sua média amostral (média=1,514). O comportamento apresentou que a maioria das observações classificadas como "Bom" estava no intervalo 1,425≤densidade≤1,514 e que a maioria das observações classificadas como "Ruim" estava no intervalo densidade<1,514 e densidade≥1,603. Assim, as observações que eram classificadas como "Bom", que não apresentavam valores no intervalo especificado (1,425≤densidade≤1,514), foram excluídas, assim como as observações que eram classificadas como "Ruim" que não apresentavam valores no intervalo especificado (densidade<1,514 e densidade≥1,603). Desta forma, a nova amostra resultou em 488 observações sobre as quais foi aplicado o segundo teste.

B. Segundo teste

A técnica de RL foi aplicada às 488 observações obtida no estudo do comportamento da amostra "densidade", assim foram excluídas 490 observações da amostra utilizada para a análise da primeira fase (978 observações). A RL foi aplicada com o auxílio do software SPSS 13.0 utilizando o método stepwise foward, para definir o modelo final que minimiza o número de variáveis e maximiza a precisão do modelo.

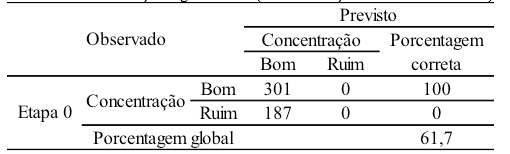
A Tabela 7 apresenta o resultado inicial considerando o modelo com apenas uma constante, ou seja, se toda a concentração fosse classificada como "Bom", a taxa de acerto seria de 61,7%, considerado insatisfatório também. O modelo de RL que irá estimar os diferentes teores de soda cáustica gerados pelas diferentes variáveis precisa ser mais assertivo na classificação dos resíduos.

Tabela 7 – Classificação segundo teste (488 observações e todas as variáveis)

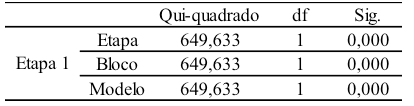
A primeira variável a ser incluída no modelo será aquela que tiver a estatística de pontuação mais alta, estatística Wald, no caso, a variável "densidade". Na tabela 8, verificamos que a análise direcionada a etapa utilizando a estatística Wald consumiu uma etapa até se obter o modelo final. Observando-se as significâncias estatísticas do modelo, constatamos que o coeficiente é significante da etapa, conforme a tabela 8.

Tabela 8 – Testes de coeficientes de modelo Omnibus

Após 20 iterações, o modelo final selecionou apenas uma variável, a "densidade", das nove variáveis incluídas inicialmente no modelo, excluindo todas as demais oito variáveis. A Tabela 9 mostra que o índice "R2 de Cox e Snell" situou-se no patamar de 73,6% e o "R2 Nagelkerke" ficou em 100%. As magnitudes das duas estatísticas são consideráveis.

Tabela 9 – Resumo do modelo

Na Tabela 10 mostra que o teste "Hosmer e Lemeshow" indica a ausência de diferença significativa na distribuição de valores dependentes efetivos e previstos. Um bom ajuste de modelo é indicado por um valor chi-quadrado não significante (HAIR et al., 2009), como o observado no modelo. Isto demostra que o modelo significante de RL.

Tabela 10 – Teste de Hosmer e Lemeshow

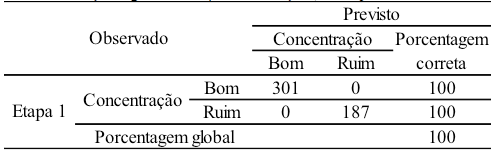
As matrizes de classificação, idênticas em natureza às utilizadas na análise discriminante (HAIR et al., 2009), mostram taxa de acerto extremamente alta de casos corretamente classificados para o modelo. Na Tabela 11, a taxa de acerto geral é de 100% e, de forma adicional, as taxas de acerto de grupos individuais são consistentemente altas e não indicam um problema na previsão de qualquer um dos dois grupos. As taxas de acerto do conjunto de padrões classificados como "Bom" é a mesma que a do conjunto de padrões classificados como "Ruim", de 100%. O modelo inicial que considerava apenas a constante tinha uma taxa geral de acerto de 61,7%. Já o modelo completo com uma variável ("densidade") apresentou a taxa de acerto de 100%.

Tabela 11 – Classificação segundo teste (488 observações, com apenas a variável "densidade")

A Tabela 12 mostra que uma variável independente é estatisticamente significativa para explicar o teor de soda cáustica contida na lama vermelha. Os coeficientes de RL das aludidas variáveis apresentam significância estatística, conforme indicado pelo teste de Wald.

Tabela 12 – Variáveis incluídas no modelo de RL (apenas a "densidade")

a = Variáveis inseridas na etapa 1: Densidade.

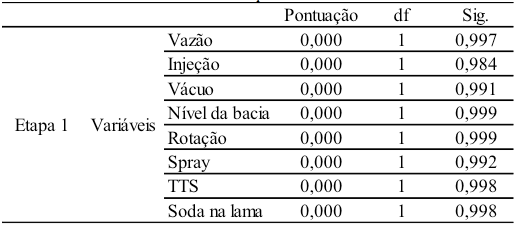
Na Tabela 13 é possível verificar que todas as variáveis que não foram incluídas no modelo, exibiram coeficientes que são, estatisticamente, iguais a zero, ou seja, (p>0,05) e, consequentemente, não exercem impacto sobre o resultado final (classificação "Bom" ou "Ruim").

Tabela 13 - Variáveis não presentes no modelo de RL

6. Conclusão

O presente trabalho utilizou a análise exploratória dos dados e a RL, enquadradas no processo KDD, a fim de identificar no rejeito do processo de produção de alumina (teor de soda cáustica na lama vermelha), os padrões das variáveis de entrada que controlam o processo.

Foram identificadas as variáveis que interferem no controle do teor cáustico do rejeito do processo e que foram utilizadas como variáveis de entrada do procedimento de classificação e previsão deste trabalho. É possível afirmar que o modelo de RL pode ser eficiente para a previsão do teor de soda cáustica contida na lama vermelha a partir de variáveis contidas no modelo.

Visando obter o melhor desempenho possível para a técnica de RL, foram realizados dois testes: em um primeiro teste foi aplicado o modelo de RL a uma amostra de dados com 978 observações, cujos resultados não foram satisfatórios. Em um segundo teste foi utilizada uma amostra de 488 observações, com a qual obteve-se uma taxa de acerto geral do modelo de RL de 100%, com a seleção de apenas uma variável, a "densidade".

Com base na classificação eficiente, poderemos utilizar o modelo de RL para prever a classificação de novos padrões. Caso a previsão indique que o padrão ainda em formação vá ser de qualidade "Ruim", a ideia seria interferir nas variáveis de entrada, a um mínimo custo, para que o processo forneça um produto (teor de soda cáustica) de qualidade "Bom".

Referências bibliográficas

ASSOCIAÇÃO BRASILEIRA DO ALUMÍNIO. Disponível em: <http://www.abal.org.br>. Acesso em: fev./ 2013.

CARDOSO, O.N.P.; MACHADO, R.T.M. (2008); Gestão do conhecimento usando data mining: estudo de caso na Universidade Federal de Lavras. Revista de Administração Pública, v.42, n.3, p.495-528.

CHAVES, A.G.F. (1962); A lama vermelha e sua eliminação da fábrica de alumina, In: 2° semana de estudos. Alumínio e Zinco. Sociedade de Intercâmbio Cultural e Estudos Geológicos dos Alunos da Escola de Minas de Ouro Preto, n. 2, Ouro Preto, Minas Gerais.

CRICHTON, N. (2001); Wald test. Journal of Clinical Nursing, v.10, p.697-706.

FAYYAD, U.M.; SHAPIRO, G.P.; SMYTH, P. (1996); From data mining to knowledge discovery: an overview. In: Fayyad UM, Shapiro GP, Smyth P, Uthursamy R, editors. Advances in knowledge discovery and data mining. Cambridge: The MIT Press/London: AAAI Press; p. 1-34.

FAYYAD, U.M.; PIATETSKY–SHAPIRO, G.; SMYTH, P. (1996); Knowledge discovery and data mining: towards a unifying framework. Proceeding of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, Oregon, august.

GAUCH, H.G. (1982); Multivariate analysis in community ecology. Cambridge: Cambridge Univ. Press.

HAIR, J.F.; BLACK, W.C.; BABIN, B.J.; ANDERSON, R.E.; TATHAM, R.L. (2009); Análise multivariada de dados. 6. ed. Porto Alegre: Bookman.

HAUCK, W.W.; DONNER, A. (1977); Wald's test as applied to hypotheses in logit analysis. Journal of the American Statistical Association, v.72, n.360a, p.851-853.

HILSON, G.; MURCK, B. (2000); Sustainable development in the mining industry: clarifying the corporate perspective. Resources Policy, v.26, p.227-238.

HIND, R.A.; BHARGAVA, S.K.; GROCOTT, S.C. (1999); The surface chemistry of Bayer process solids: a review. Colloids and surfaces A: physicochemical and engineering aspects, n.146, p.359-374. 

HINES, W.W. (2006); Probabilidade e estatística na en­genharia. 4. Ed., tradução de Vera Regina Lima de Farias e Flores, Rio de Janeiro.

HOSMER, D.W.; LEMESHOW, S. (2000); Applied logistic regression. New York: Wiley & Sons.

INTERNATIONAL ALUMINIUM INSTITUTE (IAI) Disponível em <http://www.worldaluminium. org/>.  Acesso em Fev./13.

KUSIAK, A.; KERN, J.A.; KERNSTINE, K. H.; TSENG, B.T.L. (2000); Autonomous decision making a data mining approach. IEEE Trans Inf Technol Biomed, v.4, n.4, p.274-284.

LINARES, K.S.C. (2003); Aspectos teóricos do data mining: descoberta do conhecimento em medicina (Tese de Doutorado). Florianópolis: Universidade Federal de Santa Catarina.

LUZ, A.B. (2003); Rochas e minerais industriais, Editora CETEM/MCT, Rio de Janeiro.

LUZ, A.B.; LINS, F.A.F. (2005); Rochas & minerais industriais: usos e especificações. 2. ed. Rio de Janeiro: CETEM/MCT.

MCDONALD, J. M.; BROSSETTE, S.; MOSER, S. A. (1998); Pathology information systems, data mining leads to knowledge discovery. Archives of Pathology & Laboratory Medicine, v.122, n.5, p.409-11.

MCLELLAN, B.C.; CORDER, G.D.; GIURCO, D.; GREEN, S. (2009); Incorporating sustainable development in the design of mineral processing operations – review and analysis of current approaches. Journal of Cleaner Production, v.17, p.1414-1425.

MOTA, J.F. (2007); Um estudo de caso para a determinação do preço de venda de imóveis urbanos via redes neurais artificiais e métodos estatísticos multivariados (Dissertação de Mestrado). Curitiba: Universidade Federal do Paraná.

OLIVEIRA FILHO, A.T.; FONTES, M.A.L. (2000); Patterns of floristic differentiation among Atlantic Forests in Southeastern Brazil and the influence of climate. Biotropica, v.32, n.4, p.793-810.

PIELOU, E.C. (1984); The interpretation of ecological data: a primer on classification and ordination. New York: John Wiley & Sons Publ.

SANTOS, R.M.; VIEIRA, F.A.; FAGUNDES, M.; NUNES, Y.R.F.; GUSMÃO, E. (2007); Riqueza e similaridade florística de oito remanescentes florestais no norte de Minas Gerais, Brasil. Revista Árvore, v.31, n.1, p.135-144.

SCUDELLER, V.V.; MARTINS, F.R.; SHEPHERD, G.J. (2001); Distribution and abundance of arboreal species in the atlantic ombrophilous dense forest in Southeastern Brazil. Plant Ecology, v.152, n.2, p.185-199.

STEINER, M.T.A.; NETO, A.C.; BRAULIO, S. N.; ALVES, A.C. (2008); Métodos estatísticos multivariados aplicados à engenharia de avaliações. Gestão Produção, v.15, n.1, p.23-32.

TAN, P. N.; STEINBACH, M.; KUMAR, V. (2009); Introdução ao data mining mineração de dados. Rio de Janeiro: Ciência Moderna.

TOLEDO, L.O.; ANJOS, L.H.C.; COUTO, W.H.; CORREIA, J.R.; PEREIRA, M.G.; CORREIA, M.E.F. (2009); Análise multivariada de atributos pedológicos e fitossociológicos aplicada na caracterização de ambientes de cerrado no norte de Minas Gerais. Revista Árvore, v.33, n.5, p.957-968.

1. Pontifícia Universidade Católica do Paraná - PUCPR – Brasil carla.rosa@pucpr.br

2. Pontifícia Universidade Católica do Paraná - PUCPR – Brasil cleina.okoshi@pucpr.br

3. Pontifícia Universidade Católica do Paraná - PUCPR – Brasil maria.steiner@pucpr.br
4. Pontifícia Universidade Católica do Paraná - PUCPR – Brasil ruyrgs@gmail.com

5. Pontifícia Universidade Católica do Paraná - PUCPR – Brasil wesley.vieira@pucpr.br